Навигация
Тензорные произведения операторов. Определим тензорное произведение ограниченных операторов
3.2. Тензорные произведения операторов. Определим тензорное произведение ограниченных операторов.
Теорема 3.1. Пусть ![]() ,
, ![]() - две последовательности гильбер- товых пространств,
- две последовательности гильбер- товых пространств, ![]() - последовательность операторов Ак
- последовательность операторов Ак![]() L(Нк, Gк). Определим тензорное произведение А1
L(Нк, Gк). Определим тензорное произведение А1![]() …
…![]() Аn =
Аn = ![]() Ак формулой
Ак формулой
(![]()
![]() ) f =
) f = ![]()
![]() (
(![]() ) =
) = ![]() (3.11.)
(3.11.)
(f ![]()
![]()
![]() ).
).
Утверждается, что ряд в правой части (3.11.) сходится слабо в ![]()
![]() и определяет оператор
и определяет оператор ![]()
![]()
![]() L (
L (![]()
![]() ,
, ![]()
![]() ), причем
), причем
|| ![]()
![]() || =
|| = ![]() ||
|| ![]() || (3.12.)
|| (3.12.)
Доказательство. Достаточно рассмотреть случай n=2, так как в силу равенства Н1![]() ,…,
,…, ![]() Нn = (Н1
Нn = (Н1![]() ,…,
,…, ![]() Нn-1)
Нn-1)![]() Нn общий случай получается по индукции.
Нn общий случай получается по индукции.
Пусть ![]() - некоторый ортонормированный базис в Gк (к = 1, 2) и пусть g =
- некоторый ортонормированный базис в Gк (к = 1, 2) и пусть g = ![]()
![]() G1
G1![]() G2. В качестве f возьмем вектор из Н1
G2. В качестве f возьмем вектор из Н1![]() Н2 с конечным числом отличных от нуля координат fα.
Н2 с конечным числом отличных от нуля координат fα.
Зафиксируем α2, β1 ![]() Z+ и обозначим через f(α2)
Z+ и обозначим через f(α2) ![]() Н1 вектор f(α2) =
Н1 вектор f(α2) = 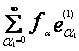 и через g(β1)
и через g(β1)![]() G2 – вектор g(β1) =
G2 – вектор g(β1) =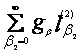 . Получим
. Получим
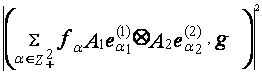 =
= 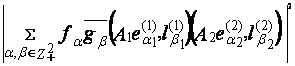 =
=
= 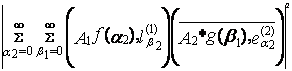 ≤
≤ 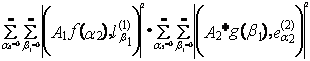 =
=
= ![]() ≤
≤ ![]() =
=
= ![]()
Из этого неравенства следует слабая сходимость в G1![]() G2 ряда
G2 ряда ![]() уже при произвольном c
уже при произвольном c ![]() Н1
Н1![]() Н2 и оценка его нормы в G1
Н2 и оценка его нормы в G1![]() G2 сверху через ||A1|| ||A2|| ||f||. Таким образом, оператор A1
G2 сверху через ||A1|| ||A2|| ||f||. Таким образом, оператор A1![]() A2: Н1
A2: Н1![]() Н2 →G1
Н2 →G1![]() G2 определен посредством (3.11.) корректно, ограничен и его норма не превосходит ||A1|| ||A2||.
G2 определен посредством (3.11.) корректно, ограничен и его норма не превосходит ||A1|| ||A2||.
Из (3.5.) и (3.11.) следует
||(A1![]() A2) (f1
A2) (f1![]() f2)|| = ||A1 f1|| ||A2 f2|| (fк
f2)|| = ||A1 f1|| ||A2 f2|| (fк ![]() Нк , к = 1, 2)
Нк , к = 1, 2)
Подбирая должным образом орты f1, f2 последнее произведение можно сделать сколь угодно близким к ||A1|| ||A2||, поэтому неравенство ||(A1![]() A2)|| ≤ ||A1|| ||A2|| не может выполняться, то есть (3.12.) при n=2 доказано.
A2)|| ≤ ||A1|| ||A2|| не может выполняться, то есть (3.12.) при n=2 доказано.
Из (3.11.) получаем для Ак ![]() L(Hк, Gк), Вк
L(Hк, Gк), Вк ![]() L(Hк, Gк) (к = 1,…, n) соотношения
L(Hк, Gк) (к = 1,…, n) соотношения
(![]() Вк) (
Вк) (![]() Ак) =
Ак) = ![]() (Вк Ак) (3.13.)
(Вк Ак) (3.13.)
(![]() Ак)* =
Ак)* = ![]() Ак* (3.14)
Ак* (3.14)
(![]() Ак) (f1
Ак) (f1![]() …
…![]() fn) = A1 f1
fn) = A1 f1![]() …
…![]() An fn (3.15.)
An fn (3.15.)
(fк ![]() Hк; к = 1,…, n)
Hк; к = 1,…, n)
(3.15) однозначно определяет оператор ![]() Ак.
Ак.
Приведем пример. Пусть Hк = L2(![]() (0,1), d (
(0,1), d (![]() mк)) = L2
mк)) = L2
Действительно, вектору вида (3.1.) ![]()
![]()
![]()
![]() поставим в соответствие функцию
поставим в соответствие функцию ![]()
![]() L2. Такие функции образуют ортонормированный базис пространства L2, поэтому такое соответствие порождает требуемый изоморфизм между
L2. Такие функции образуют ортонормированный базис пространства L2, поэтому такое соответствие порождает требуемый изоморфизм между ![]()
![]() и L2.
и L2.
Глава II. Задача о двух ортопроекторах
§ 1. Два ортопроектора в унитарном пространстве
Постановка задачи. Пусть дана *-алгебра P2
P2 = С < р1, р2 | р12 = р1* = р1, р22 =р2* = р2 >
порожденная двумя проекторами, то есть двумя идемпотентными самосопряженными элементами.
Положим u = 2p1 – 1, v = 2p2 – 1, тогда u, v самосопряженные элементы.
u2 = (2p1 – 1)2 = 4p1 – 4p1 + 1 = 1, v2 = 1. Таким образом u, v – унитарные самосопряженные элементы.
Тогда *-алгебру P2 можно задать иначе:
P2 = С < p1*= p1, p2*=p2 | p12 = p1, p22 = p2 > = C <u* = u, v* = v | u2 = 1, v2 =1 >
Это групповая *-алгебра, порожденная двумя унитарными самосопряженными элементами.
Требуется найти все неприводимые представления *-алгебры P2 , с точностью до унитарной эквивалентности.
1.2. Одномерные *-представления *-алгебры P2 . Пусть π: P2 →L(H) - *-представление *-алгебры P2 . Рассмотрим сначала случай, когда dim H = 1, то есть dim π = 1.
P2 = С < р1, р2 | р12 = р1* = р1, р22 =р2* = р2 >
Обозначим через Рк = π(рк), к = 1,2. Поскольку рк2= рк* = рк (к = 1, 2) и π - *-представление, то Рк2 = Рк* = Рк (к =1, 2) – ортопроекторы в Н на подпространстве Нк = {y![]() H | Рк y = y } к = 1, 2.
H | Рк y = y } к = 1, 2.
Возможны следующие случаи:
Н1 = Н2 = {0}; тогда Р1 = 0, Р2 = 0.
Н1 = Н (то есть dim H1 =1), Н2 = {0}, тогда Р1 = 1, Р2 = 0.
Н1 = {0}, Н2 = Н (то есть dim H2 =1), тогда Р1 = 0, Р2 = 1.
Н1 = Н2 = Н (dim H1 = dim H2 =1), тогда Р1 = 1, Р2 = 1.
Так как dim H =1, то мы можем получить 4 одномерных неприводимых *-представлений P2, причем они неэквивалентны.
1.3. Двумерные *-представления *-алгебры P2 . Обозначим через Нк область значений оператора Рк при к = 1,2. Пусть Нк┴ - ортогональное дополнение подпространства Нк (к = 1,2) в Н. Тогда Н=H1![]() Н1┴ , Н=H2
Н1┴ , Н=H2![]() Н2┴
Н2┴
Введем дополнительные обозначения :
Н0,0 = Н1┴ ∩Н2┴, Н0,1 = Н1┴ ∩Н2, Н1,0 = Н1 ∩Н2┴, Н1,1 = Н1 ∩Н2. (1.1.)
Пусть dim H = 2. предположим, что существуют i и j такие, что Hij нетривиально, то есть dim Hij =1. Пусть, например, dim Н1,0 = 1 (остальные случаи аналогичны). Тогда в H существует ненулевой вектор h такой, что Н1,0 = л.о. {h}, но тогда P1h = h, P2h = 0; следовательно Н1,0 инвариантное подпространство. Значит в этом случае *-представление π не может быть неприводимым.
Будем считать, что Hij ={0} для любых i = 0, 1 и j =0, 1, (то есть Hij линейно независимы) и dim H1 = dim H2 =1. Тогда в Н можно найти два ортогональных базиса {e1, e2} и {g1, g2}, в которых матрицы операторов Р1 и Р2 имеют вид ![]() . Найдем матрицу оператора Р2 в базисе {e1, e2}.
. Найдем матрицу оператора Р2 в базисе {e1, e2}.
![]() Пусть g1 = a11e1 + a12 e2
Пусть g1 = a11e1 + a12 e2
![]() g2 = a21e1 + a22e2
g2 = a21e1 + a22e2
e1 = b11g1 + b12g2
e2 = b21g1 + b22g2
Рассмотрим векторы h1 = eite1 и h2 = eile2, тогда
|| h1 || = || eite1 || = || e1 || = 1, || h2 || = || eile2 || = || e2 || = 1
(h1 ,h2 ) = (eite1 , eile2) = ei(t-l)(e1, e2 ) = 0, то есть {h1 ,h2} – ортонормированный базис.
Р1h1 =ei t Р1 e1 = h1, Р1h2 =eil Р1 e2 = 0.
Значит в базисе {h1 ,h2} матрица оператора Р1 также имеет вид ![]() . Тогда можно считать, что a11, a12 > 0 (так как, например, a11 e1=|a11| eite1 =|a11| h1)
. Тогда можно считать, что a11, a12 > 0 (так как, например, a11 e1=|a11| eite1 =|a11| h1)
(e1, e2 ) = 0, значит a11 a21 = a12 a22 = 0 или 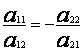 , тогда существует такое комплексное число r, что
, тогда существует такое комплексное число r, что
![]() a22 = - ra11
a22 = - ra11
a21 = ra12
Базис (e1, e2 ) ортонормированный; следовательно
![]() a112 + a122 = 1
a112 + a122 = 1
|a22 |2 + |a21 |2 = 0
тогда | r | = 1.
Р2 e1 = Р2 ( b11g1 + b12g2) = b11g1 = b11a11e1 + b11a12e2,
Р2 e2 = Р2 ( b21g1 + b22g2) = b21g1 = b21a11e1 + b21a12e2.
Найдем b11 и b21:
e1 = b11g1 + b12g2 = b11 (a11e1 + a12 e2) + b12 (a21e1 + a22e2) = (b11a11 + b12a12)e1 + (b11a12 + b12a22)e2,
![]() b11a11 + b12a12 = 1
b11a11 + b12a12 = 1
b11a12 + b12a22 = 0 или
![]() b11a11 + b12a12 r = 1
b11a11 + b12a12 r = 1
b11a12 - b12a11 r = 0,
Тогда b11 = a11.
Аналогично
E2 = b21g1 + b22g2 = (b21a11 + b22a21)e1 + (b21a12 + b22a22)e2,
![]() b21a11 + b22a21= 0
b21a11 + b22a21= 0
b21a12 + b22a22 = 1,
отсюда находим, что b21 = a12.
Тогда матрица оператора Р2 в базисе {e1, e2 } будет иметь вид (обозначим ее также через Р2)
Р2 = 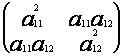 , где a11>0, a12>0 и a112 + a122 =1
, где a11>0, a12>0 и a112 + a122 =1
А) Пусть a112 = τ, тогда a122 =1 – τ, a11a12 = ![]() . Так как a11a12 >0, то τ
. Так как a11a12 >0, то τ![]() (0, 1).
(0, 1).
Тогда Р2 = 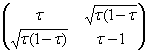 .
.
В) Положим a11 = cosφ,тогда a12 = sinφ и Р2 запишется следующим образом
Р2 = 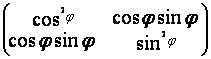 .
.
Найдем коммутант π(P2). Пусть Т = ![]() оператор перестановочный с Р1 и Р2, тогда
оператор перестановочный с Р1 и Р2, тогда
ТР1 = ![]()
![]() =
= ![]()
Р1Т = ![]()
![]() =
= ![]()
Следовательно b = c = 0.
ТР2 = ![]()
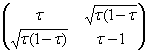 =
= 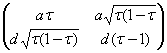
Р2Т = 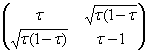
![]() =
= 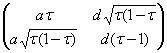
Следовательно a = d. Тогда Т скалярный оператор и по лемме Шура (теорема 2.6. глава I) представление π неприводимо.
Покажем, что все эти представления неэквивалентны.
Пусть τ, ν![]() (0, 1), τ ≠ ν. Предположим, что существует унитарный оператор в Н, устанавливающий эквивалентность. Тогда
(0, 1), τ ≠ ν. Предположим, что существует унитарный оператор в Н, устанавливающий эквивалентность. Тогда
UР1 = Р1U, следовательно U= ![]() , a, b
, a, b ![]() C
C
UР2 (τ) = ![]()
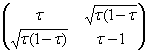 =
= 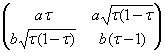
Р2 (ν) U = 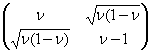
![]() =
= 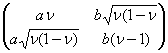 .
.
Тогда τ = ν, следовательно U = 0 и представления неэквивалентны.
Теорема 1.1. Пусть π: P2 →L(H) - *-представление *-алгебры P2 .
Тогда:
(i) Все одномерные и неэквивалентные представления имеют вид: π0,0(p1) = 0; π0,0(p2) = 0; π1,0(p1) = 1; π1,0(p2) = 0; π0,1(p1) = 0; π0,1(p2) = 1; π1,1(p1) = 1; π1,1(p2) = 1;
(ii) Все двумерные неприводимые и неэквивалентные представления имеют вид: π(p1) ![]() , π(p2)
, π(p2) 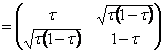 τ
τ![]() (0, 1).
(0, 1).
Доказательство следует из сказанного выше и в пункте (ii) можно положить π(p2) = 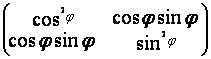 φ
φ![]() (0,
(0, ![]() ).
).
1.4. n – мерные *-представления *-алгебры P2 . Рассмотрим случай нечетной размерности пространства Н. Если dimН=2n+1, где n>1 натуральное, то выполняется неравенство
max (dimН1, dimН1┴) + max (dimН2, dimН2┴) > 2n+1 (1.4.)
Тогда обязательно найдутся такие i = 0,1 и j= 0,1, что Нi,j ≠ {0}, следовательно, существует нетривиальное инвариантное подпространство относительно *-представления π, но тогда π приводимо.
Пусть теперь dimН=2n, n>1 натуральное. Будем считать, что dimН1 = n, dimН2 = n и Нi,j = {0} для любых i = 0,1 и j= 0,1, то есть Нi,j линейно независимы. Если это не так, то снова будет выполнятся неравенство (1.4.) и *-представление π окажется приводимым. При этих условиях справедлива лемма.
Лемма 1.1. Существует х ≠ 0, х![]() Н1 такой, что Р1Р2х = λх, где λ
Н1 такой, что Р1Р2х = λх, где λ![]() С.
С.
Доказательство. Пусть ![]() ,
, ![]() ортонормированный базисы в Н, в которых матрицы операторов Р1 и Р2 имеют вид
ортонормированный базисы в Н, в которых матрицы операторов Р1 и Р2 имеют вид ![]() , где I – единичная матрица порядка n. Пусть базисы (е) и (g) связаны уравнениями
, где I – единичная матрица порядка n. Пусть базисы (е) и (g) связаны уравнениями
![]()
![]()
![]()
![]()
к = 1,…, n к = 1,…, n
Так как х![]() Н1, то
Н1, то ![]() , gk
, gk ![]() C, к = 1,…, n. Тогда
C, к = 1,…, n. Тогда
Р1Р2х = Р1Р2![]() = Р1Р2
= Р1Р2![]()
![]() = Р1
= Р1![]()
![]() =
=
= Р1![]()
![]()
![]() =
= ![]()
![]()
![]() =
= ![]() (
(![]()
![]() )
)![]() =
= ![]()
Таким образом получаем систему линейных однородных уравнений относительно q1,…, qn:
![]()
![]()
![]() =
= ![]()
j = 1,…, n
Подбирая λ![]() C так, чтобы определитель этой системы обратился в нуль, получим ненулевое решение q1,…, qn. Это доказывает лемму.
C так, чтобы определитель этой системы обратился в нуль, получим ненулевое решение q1,…, qn. Это доказывает лемму.
Лемма 1.2. Пусть элемент х удовлетворяет условиям леммы 15. Тогда L=л.о. {х, Р2х} – инвариантное подпространство в Н относительно Р1 и Р2.
Доказательство. Проверим инвариантность L. Для любых a, b ![]() С имеем
С имеем
Р1 (aх + bР2х) = aх + λbх = (a + λb) х ![]() L,
L,
Р2 (aх + bР2х) = aР2х + bР2х = (a + b) Р2 х ![]() L
L
dimL = 2, так как Нi,j = {0} (для всех i, j= 0,1).
Действительно, если aх + bР2х = 0, где, например, а ≠ 0, то х = ![]() Р2х, значит
Р2х, значит ![]() = 0 или 1 и х
= 0 или 1 и х ![]() Н1,1; тогда Н1,1≠{0}.
Н1,1; тогда Н1,1≠{0}.
Итак, получаем предложение.
Теорема 1.2. Если dimН = n, n>2, то нет неприводимых *-пред- ставлений *-алгебры P2 . Все неприводимые конечномерные *-представления одномерны и двумерны.
1.5. Спектральная теорема. Пусть dimН = n. В этом пункте мы получим разложение на неприводимые *-подпредставления исходного *-представления π *-алгебры P2, а также разложение пространства Н на инвариантные подпространства относительно π.
Теорема 3.1. (спектральная теорема). Существует единственное разложе- ние Н в ортогональную сумму инвариантных относительно Р1 и Р2 подпространств
Н = Н0,0![]() Н0,1
Н0,1![]() Н1,0
Н1,0![]() Н1,1
Н1,1 ![]() (
(![]() (С2
(С2![]() Нк)), (1.1.)
Нк)), (1.1.)
где каждому подпространству Нк соответствует одно φк![]() (0,
(0, ![]() ), φк ≠ φi при к≠i, dimНк = nк (к = 1,…, m). Пусть Рi,j: Н → Нi,j , Рφк: Н → С2
), φк ≠ φi при к≠i, dimНк = nк (к = 1,…, m). Пусть Рi,j: Н → Нi,j , Рφк: Н → С2![]() Нк – ортопроекторы к = 1,…, m. Тогда существуют единственные разложения операторов
Нк – ортопроекторы к = 1,…, m. Тогда существуют единственные разложения операторов
I = P0,0![]() P0,1
P0,1![]() P1,0
P1,0 ![]() P1,1
P1,1![]() (
(![]() Рφк), (1.2.)
Рφк), (1.2.)
P1 = P1,0![]() P1,1
P1,1![]() (
(![]() (
(![]()
![]() Iк )) (1.3)
Iк )) (1.3)
Р2 = P0,1 ![]() P1,1
P1,1 ![]() (
(![]()
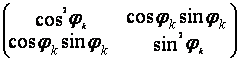
![]() Iк )) (1.4)
Iк )) (1.4)
где Iк – единичный оператор на Нк (к = 1,…, m).
Доказательство. Пусть dimНi,j = ni,j. Сразу можем записать разложение
Н = Н0,0![]() Н0,1
Н0,1![]() Н1,0
Н1,0 ![]() Н1,1
Н1,1 ![]() Н΄, где dimН΄ четное число. Используя лемму 1.2. и теорему 2.1. главы I можем написать разложение Н΄ в ортого- нальную сумму инвариантных двумерных подпространств, определяемых параметром φк
Н΄, где dimН΄ четное число. Используя лемму 1.2. и теорему 2.1. главы I можем написать разложение Н΄ в ортого- нальную сумму инвариантных двумерных подпространств, определяемых параметром φк![]() (0,
(0, ![]() ):
):
Н΄ = ![]() Нφк, (l = n -
Нφк, (l = n - ![]() )
)
Собирая вместе все Нφк, у которых одно φк, получим изоморфизм
Нφк![]() …
…![]() Нφк ≈ С2
Нφк ≈ С2![]() Нк , где Нφк nк экземпляров, dim(Нφк
Нк , где Нφк nк экземпляров, dim(Нφк![]() …
…![]() Нφк )=2nк dim(С2
Нφк )=2nк dim(С2![]() Нк) = dimС2 dimНк = 2nк . Следовательно, получаем разложение (1.1.)
Нк) = dimС2 dimНк = 2nк . Следовательно, получаем разложение (1.1.)
Н = Н0,0 ![]() Н0,1
Н0,1![]() Н1,0
Н1,0 ![]() Н1,1
Н1,1 ![]() (
(![]() (С2
(С2![]() Нк))
Нк))
Пусть πi,j – сужение π на Нi,j ( i, j= 0,1), πк – сужение π на Нφк (к = 1,…, m), то есть πi,j и πк - *-подпредставления.
Учитывая кратности подпредставлений получаем
π = n0,0π0,0![]() n0,1π0,1
n0,1π0,1![]() n1,0π1,0
n1,0π1,0![]() n1,1π1,1
n1,1π1,1![]() (
(![]() nкπк) (1.5.)
nкπк) (1.5.)
В силу теоремы 2.8. главы I разложения (1.1.) и (1.5.) единственные.
Из (1.1.) следует разложение единичного оператора I (1.2.)
I = P0,0 ![]() P0,1
P0,1![]() P1,0
P1,0 ![]() P1,1
P1,1 ![]() (
(![]() Рφк)
Рφк)
Тогда ортопроекторы Р1 и Р2 примут вид
P1 = P1,0 ![]() P1,1
P1,1 ![]() (
(![]() (
(![]()
![]() Iк ))
Iк ))
Р2 = P0,1 ![]() P1,1
P1,1 ![]() (
(![]()
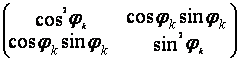
![]() Iк ))
Iк ))
Причем n1,0π1,0(р1) = P1,0 , n0,1π0,1(p2) = P0,1 , n1,1π1,1(р1) = P1,1 , n0,0π0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно.
§ 2. Два ортопроектора в сепарабельном гильбертовом пространстве
2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА = АUА = А2ВА = ВА = U-1, следовательно
UА = АU-1 или АU = U-1А (2.1.)
Лемма 2.1. Операторы А и В неприводимы тогда и только тогда, когда операторы А и U неприводимы.
Доказательство. Допустим, что А и В неприводимы. Пусть существует нетривиальное инвариантное подпространство L относительно операторов А и U. Тогда UL = АВL![]() L, но тогда ВL
L, но тогда ВL![]() АL
АL![]() L, то есть пара А, В – приводима.
L, то есть пара А, В – приводима.
Обратно, пусть А и U неприводимы. Если операторы А и В приводимы, то есть ![]() L
L![]() Н: АL
Н: АL![]() L и ВL
L и ВL![]() L, то из включения АВL
L, то из включения АВL![]() АL
АL![]() L следует приводимость А и U, что невозможно.
L следует приводимость А и U, что невозможно.
Лемма 2.2. Ортопроекторы Р1 и Р2 неприводимы тогда и только тогда, когда А и В неприводимы.
Доказательство. Пусть Р1 и Р2 приводимые операторы, когда существует нетривиальное инвариантное подпространство L![]() Н такое, что Р1L
Н такое, что Р1L![]() L, Р2L
L, Р2L![]() L. Рассмотрим АL = (2Р1 – I)L
L. Рассмотрим АL = (2Р1 – I)L![]() L, ВL = (2Р2 – I)L
L, ВL = (2Р2 – I)L![]() L, то есть А и В приводимы.
L, то есть А и В приводимы.
Обратно, пусть А и В приводимые операторы, тогда Р1 и Р2 также будут приводимы, так как Р1L = ![]() L
L![]() L, Р2L =
L, Р2L = ![]() L
L![]() L, для любого инвариантного относительно А и В подпространства L в Н.
L, для любого инвариантного относительно А и В подпространства L в Н.
Лемма 2.3. Если eiφ![]()
![]() (U), то e-iφ
(U), то e-iφ![]()
![]() (U).
(U).
Доказательство.
1) Если eiφ принадлежит точечному спектру оператора U, то существует f![]() Н: ||f|| = 1 и Uf = eiφ f. Тогда по (2.1.) UАf = АU-1f = eiφАf, следовательно, Аf собственный вектор оператора U, то есть e-iφ принадлежит спектру U.
Н: ||f|| = 1 и Uf = eiφ f. Тогда по (2.1.) UАf = АU-1f = eiφАf, следовательно, Аf собственный вектор оператора U, то есть e-iφ принадлежит спектру U.
2) Если eiφ![]()
![]() (U), то существует последовательность единичных векторов
(U), то существует последовательность единичных векторов ![]() в Н || fn || = 1 такая, что
в Н || fn || = 1 такая, что
||Ufn - eiφfn || = || UАfn - eiφ A fn || = || U-1Аfn - eiφ A fn || → 0 при n → ∞ (|| Аfn || =1)
Тогда eiφ![]()
![]() (U-1), следовательно e-iφ
(U-1), следовательно e-iφ![]()
![]() (U).
(U).
Теорема 2.1. Неприводимые пары А и В самосопряженных операторов лишь одномерны и двумерны.
Доказательство. Рассмотрим соотношения
А (U + U-1) = АU + АU-1 = (U-1 +U)А
А (U - U-1) = А (U2 – 2I + U-2) = (U2 – 2I + U-2)А = (U - U-1)2А
Таким образом А (U + U-1) = (U-1 +U)А (2.2.)
А (U - U-1) = (U - U-1)2А (2.3.)
Пара А и U неприводима (лемма 2.1.), тогда по теореме 2.6. главы I имеем
U + U-1 = cI
(U - U-1)2 = d2I
где c, d ![]() С. По теореме преобразования спектров eiφ+ e-iφ = c, eiφ- e-iφ = ±d.
С. По теореме преобразования спектров eiφ+ e-iφ = c, eiφ- e-iφ = ±d.
Если d = 0, то ![]() (U) состоит из одной точки eiφ, где φ=0 или φ=π, и U = I или U = -I. Так как А, U неприводимая пара, то dimН=1 и А = +I или А = -I. Поскольку существует одномерное инвариантное подпространство y оператора А: л.о. {(A+I)x}, х
(U) состоит из одной точки eiφ, где φ=0 или φ=π, и U = I или U = -I. Так как А, U неприводимая пара, то dimН=1 и А = +I или А = -I. Поскольку существует одномерное инвариантное подпространство y оператора А: л.о. {(A+I)x}, х![]() H.
H.
Если d ≠ 0, то ![]() (U) дискретен и состоит из двух точек eiφ=
(U) дискретен и состоит из двух точек eiφ=![]() и e-iφ=
и e-iφ=![]() φ
φ![]() (0, π)
(0, π)
Собственное подпространство оператора U, отвечающее собственному значению eiφ (или e-iφ), Нeiφ = {f![]() H | Uf = eiφf} одномерно. Действительно, подпространство, натянутое на собственные векторы f и Af для оператора U: Uf = eiφf, U(Аf) = eiφ Аf инвариантно относительно операторов U и А. U и А неприводимы, значит dimНeiφ= dimН-eiφ=1
H | Uf = eiφf} одномерно. Действительно, подпространство, натянутое на собственные векторы f и Af для оператора U: Uf = eiφf, U(Аf) = eiφ Аf инвариантно относительно операторов U и А. U и А неприводимы, значит dimНeiφ= dimН-eiφ=1
Таким образом, все неприводимые пары операторов U и А такие, что ![]() (U) = {eiφ, e-iφ} φ
(U) = {eiφ, e-iφ} φ![]() (0, π) в базисе из собственных векторов оператора U имеют вид:
(0, π) в базисе из собственных векторов оператора U имеют вид:
А = ![]() , U =
, U =  , В =
, В = 
Теорема 2.2. Неприводимые пары Р1, Р2 ортопроекторов лишь одномер- ны и двумерны.
Доказательство. Сразу следует из леммы 2.2.
Похожие работы
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...
... для того, чтобы показать школьникам образец современной математической теории. 2.2.3.2. ПРОГРАММА И СОДЕРЖАНИЕ ЗАНЯТИЙ ФАКУЛЬТАТИВНОГО КУРСА «ЭЛЕМЕНТЫ СОВРЕМЕННОЙ АЛГЕБРЫ» В качестве экспериментальной работы мы предлагаем изучение элементов современной алгебры в рамках факультативного курса по математике. Нами была разработана программа факультативного курса «Элементы современной алгебры» и ...
... угодно сложные в логическом отношении схемы, можно строить, используя два приема: 1. последовательное соединение элементов; 2. перестановка входов элементов. Этим двум физическим приемам в алгебре логики соответствуют: 1. принцип суперпозиции (подстановка в функцию вместо ее аргументов других функций); 2. подстановка аргументов (изменение порядка записи аргументов функций или замена ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...

0 комментариев