Примеры
Гомоморфизм и изоморфизм алгебр
Неприводимые представления
Конечномерные представления
Тензорные произведения операторов. Определим тензорное произведение ограниченных операторов
Спектральная теорема. Пусть Н – сепарабельное гильбертово пространство, тогда справедлива следующая теорема
Спектр ортопроектора в гильбертовом пространстве
< ε < a
Спектр оператора А = Р1 + Р2. Изучим оператор Р1 + Р2 в сепарабельном гильбертовом пространстве
Навигация
< ε < a
* Алгебры и их применение
65703
знака
0
таблиц
0
изображений
0 < ε < a
Пусть dimH =n. Тогда справедлива теорема.
Теорема 1.3. Самосопряженный оператор А представим в виде линейной комбинации ортопроекоров А = aР1 + bР2, 0<a<b тогда и только тогда, когда
(А) 
{0, a, b, a + b}
(
{εк , a + b - εк}), 0<εк<1, и
dimНεк = dimНa+b-εк (Нεк , Нa+b-εк - собственные подпространства оператора А, отвечающие εк) к=1,…m.
Доказательство. Пусть А = aР1 + bР2, 0<a<b. Найдем (А).
1) х
Н0,0, то Ах = 0 и 0(А);
2) х Н0,1 , то Ах = bx и b(А);
3) х Н1,0 , то Ах = ax и a(А);
4) х Н1,1 , то Ах = (a+b)x и a+b(А).
Тогда (А) {0, a, b, a + b}({εк , a + b - εк}), где 0<εк<1, к=1,…m. Причем числа εк, a + b - εк входят одновременно в спектр А, и соответству- ющие собственные подпространства ортогональны и одномерны, так как А=А*. Тогда сумма всех собственных подпространств, отвечающих одному εк также инвариантна относительно А и dimНεк = dimНa+b-εк = qk. (с учетом кратности εк)
Обратно. Существует единственное разложение Н в силу (1.4.)
Н = Н(0)
Н(a) Н(b)Н(a+b) (
(С2
Нк)) (1.9.)
Где Н(0)=Н0,0 , Н(a) =Н1,0 , Н(b)=Н0,1 , Н(a+b)=Н1,1 или
Н = Н(0) Н(a) Н(b)Н(a+b) ((Нεк Нa+b-εк) (1.10.)
Положим
P1 = PaPa+b ((
Iк )) (1.11.)
Р2 = Pb Pa+b (
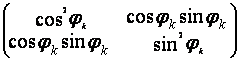
Iк )) (1.12.)
Но тогда
aР1 + bР2 = aPabPb (а+b)Pa+b (a(Iк ))
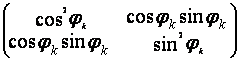
(bIк )) = A.
Спектр оператора А совпадает с {0, a, b, a + b}({εк , a + b - εк}), (0<εк<1, к=1,…m) по построению и А = А* как вещественная комбинация ортопроекторов.
§ 2. Спектр суммы двух ортопроекторов в сепарабельном гильбертовом пространстве
Похожие работы
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...
... для того, чтобы показать школьникам образец современной математической теории. 2.2.3.2. ПРОГРАММА И СОДЕРЖАНИЕ ЗАНЯТИЙ ФАКУЛЬТАТИВНОГО КУРСА «ЭЛЕМЕНТЫ СОВРЕМЕННОЙ АЛГЕБРЫ» В качестве экспериментальной работы мы предлагаем изучение элементов современной алгебры в рамках факультативного курса по математике. Нами была разработана программа факультативного курса «Элементы современной алгебры» и ...
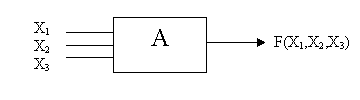
... угодно сложные в логическом отношении схемы, можно строить, используя два приема: 1. последовательное соединение элементов; 2. перестановка входов элементов. Этим двум физическим приемам в алгебре логики соответствуют: 1. принцип суперпозиции (подстановка в функцию вместо ее аргументов других функций); 2. подстановка аргументов (изменение порядка записи аргументов функций или замена ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...
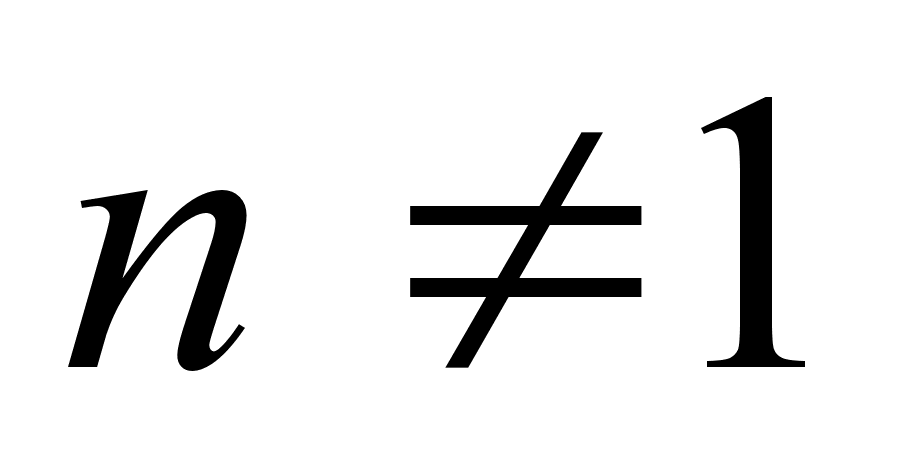
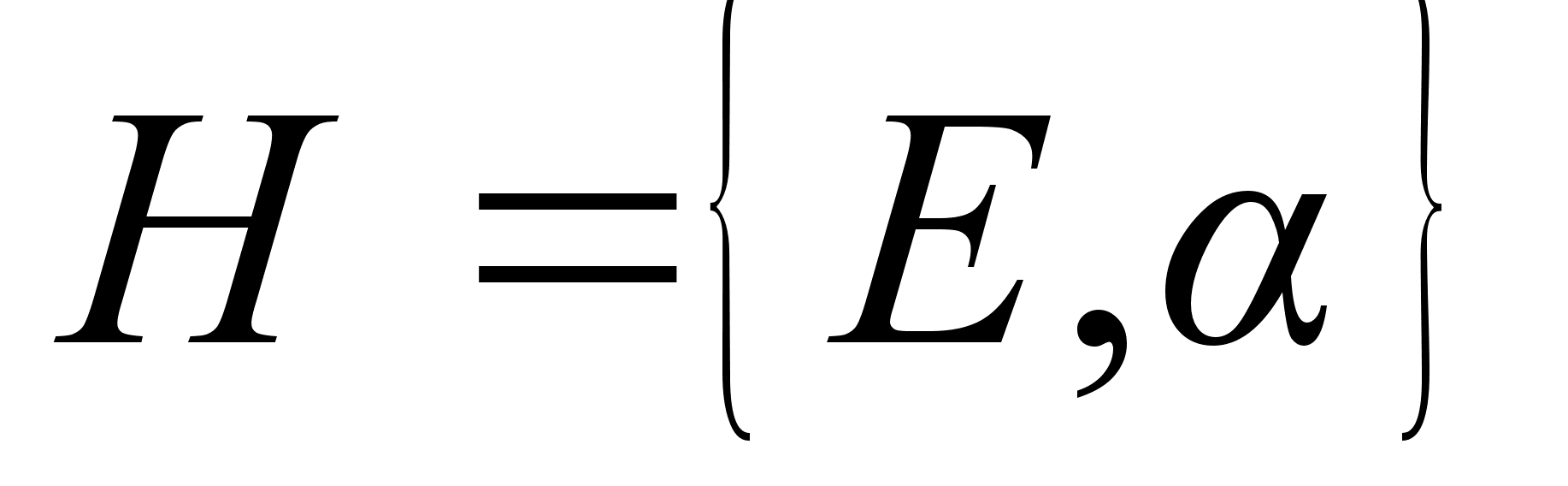
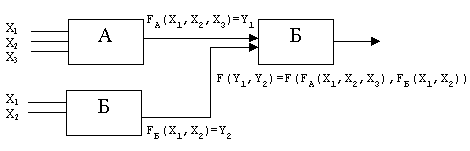
0 комментариев