Навигация
Спектр ортопроектора в гильбертовом пространстве
1.1. Спектр ортопроектора в гильбертовом пространстве.
Теорема 1.1. Пусть Н – гильбертово пространство. Если Р – ортопроектор, то ![]() (Р) =
(Р) = ![]() р (Р) = {0, 1}, где
р (Р) = {0, 1}, где ![]() р (Р) – точечный спектр при условии, что Р ≠ 0 и Р ≠ I.
р (Р) – точечный спектр при условии, что Р ≠ 0 и Р ≠ I.
Доказательство. Рассмотрим выражение Рх - λх = y, х, y![]() Н, λ
Н, λ![]() С. Тогда (1 - λ) Рх = Рy . Если λ ≠ 1, то Рх =
С. Тогда (1 - λ) Рх = Рy . Если λ ≠ 1, то Рх = ![]() Рy. Если х ≠ 1, то х =
Рy. Если х ≠ 1, то х = ![]() (
(![]() Рy - y), тогда
Рy - y), тогда ![]() (Р) = {0, 1}.
(Р) = {0, 1}.
Так как Р ≠ 0 и Р ≠ I, то существует х ≠ 0 такой, что Рх ≠ 0. Тогда Р(Рх) = Рх, то есть 1![]()
![]() р (Р). Существует y ≠ 0: (I - Р)y ≠ 0, тогда Р(I - Р)y = 0 = 0 · (I - Р)y, то есть 0
р (Р). Существует y ≠ 0: (I - Р)y ≠ 0, тогда Р(I - Р)y = 0 = 0 · (I - Р)y, то есть 0 ![]()
![]() р (Р). Итак,
р (Р). Итак, ![]() (Р) =
(Р) = ![]() р (Р) = {0, 1}.
р (Р) = {0, 1}.
1.2. Постановка задачи. Пусть заданы два ортопроектора Р1 и Р2 в унитарном пространстве Н. Тогда мы знаем спектр каждого из них. Найдем спектр суммы Р1 + Р2 в неприводимых представлениях.
1.3. Спектр в одномерном пространстве. Пусть dimH =1. Пусть, как и выше, Нк – область значений оператора Рк к = 1,2. Обозначим через А = Р1 + Р2 и найдем ![]() (А).
(А).
1) Р1 = Р2 = 0, то для любого х![]() Н Ах = 0 или Ах = 0 · х, то есть 0
Н Ах = 0 или Ах = 0 · х, то есть 0 ![]()
![]() (А).
(А).
2) Р1 = 0, Р2 = I, то для любого х![]() Н2 = Н Ах = х, то есть 1
Н2 = Н Ах = х, то есть 1 ![]()
![]() (А).
(А).
3) Р1 = I, Р2 = 0, то для любого х![]() Н1 = Н Ах = х.
Н1 = Н Ах = х.
4) Р1 = Р2 = I, то для любого х![]() Н1 = Н2 = Н Ах = Р1х + Р2х = 2х, то есть 2
Н1 = Н2 = Н Ах = Р1х + Р2х = 2х, то есть 2 ![]()
![]() (А).
(А).
Таким образом, если dimH =1, то ![]() (А)
(А) ![]() {0, 1, 2}.
{0, 1, 2}.
1.4. Спектр в двумерном пространстве. Пусть dimH =2. Сохраним обозначения (1.1.) Главы II.
1) х![]() Н0,0 , тогда Ах = 0 и 0
Н0,0 , тогда Ах = 0 и 0 ![]()
![]() (А).
(А).
2) х![]() Н0,1 или х
Н0,1 или х![]() Н1,0 , тогда Ах = х и 1
Н1,0 , тогда Ах = х и 1 ![]()
![]() (А).
(А).
3) х![]() Н1,1, тогда Ах = 2х, то есть 2
Н1,1, тогда Ах = 2х, то есть 2 ![]()
![]() (А).
(А).
Если существуют i, j= 0,1 такие, что Нi,j ≠ {0}, то существуют k,l = 0,1 такие, что Нi,j ![]() Нk,l = H. В этом случае
Нk,l = H. В этом случае ![]() (А)
(А) ![]() {0, 1, 2}.
{0, 1, 2}.
Пусть теперь Нk,l = {0} для любых k,l = 0,1. Допустим, что существует одномерное инвариантное подпространство L относительно Р1 и Р2, тогда АL![]() L. Пусть х
L. Пусть х![]() L, тогда Рkх = λкх (k = 1, 2 ). Так как Рk ортопроектор, то возможны случаи:
L, тогда Рkх = λкх (k = 1, 2 ). Так как Рk ортопроектор, то возможны случаи:
λ1 = 0, λ2 = 0;
λ1 = 0, λ2 = 1;
λ1 = 1, λ2 = 0;
λ1 = 1, λ2 = 1;
Но это означает, что ![]() k,l = 0,1 такие, что Нk,l ≠ {0} вопреки предположению. Тогда пара Р1, Р2 неприводима. Значит мы можем записать матрицы операторов Р1 и Р2 в некотором ортонормированном базисе, согласно теореме 1.1. главы II.
k,l = 0,1 такие, что Нk,l ≠ {0} вопреки предположению. Тогда пара Р1, Р2 неприводима. Значит мы можем записать матрицы операторов Р1 и Р2 в некотором ортонормированном базисе, согласно теореме 1.1. главы II.
Р1 = ![]() , Р2
, Р2 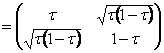 τ
τ![]() (0, 1)
(0, 1)
Найдем спектр линейной комбинации ортопроекторов aР1 + bР2, a и b![]() С. Для этого решим характеристическое уравнение det(aР1 + bР2 – λI) = 0.
С. Для этого решим характеристическое уравнение det(aР1 + bР2 – λI) = 0.
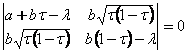
![]() (1.1.)
(1.1.)
Тогда 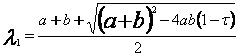 ,
, 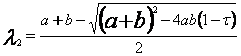 (1.2)
(1.2)
Положим a = 1, b =1, ε = ![]() , тогда λ1 = 1+ε , λ2 = 1-ε и 0<ε<1 (поскольку 0<τ<1.
, тогда λ1 = 1+ε , λ2 = 1-ε и 0<ε<1 (поскольку 0<τ<1.
Тогда ![]() (А)
(А) ![]() {0, 1, 2}
{0, 1, 2}![]() {1+ε , 1-ε}. Причем собственные значения 1+ε и 1-ε входят в спектр А одновременно.
{1+ε , 1-ε}. Причем собственные значения 1+ε и 1-ε входят в спектр А одновременно.
1.5. Спектр в n-мерном пространстве. Пусть dimH =n. Если Н =К![]() L, где К, L инвариантные подпространства относительно оператора А, то для любого х
L, где К, L инвариантные подпространства относительно оператора А, то для любого х![]() Н существует единственное разложение x = k +l, k
Н существует единственное разложение x = k +l, k![]() K, l
K, l![]() L. Пусть λ
L. Пусть λ![]()
![]() (А), тогда Ах = λх =λk +λl;, следовательно, если пространство Н разложено в ортогональную сумму инвариантных подпространств, то спектр оператора А можно найти как объединение спектров сужений оператора А на соответствующие инвариантные подпространства.
(А), тогда Ах = λх =λk +λl;, следовательно, если пространство Н разложено в ортогональную сумму инвариантных подпространств, то спектр оператора А можно найти как объединение спектров сужений оператора А на соответствующие инвариантные подпространства.
Используя лемму 1.2. главы II, представим Н в виде ортогональной суммы подпространств Н0 = Н0,0, Н1=Н0,1![]() Н1,0, Н2=Н1,1 и двумерных, инвариантных относительно А, подпространств Нφк φк
Н1,0, Н2=Н1,1 и двумерных, инвариантных относительно А, подпространств Нφк φк![]() (0,
(0, ![]() ), (к = 1,…, s). При этом операторы Р1 и Р2 неприводимы в Нφк (к = 1,…, s), и собственные значения 1+εк, 1-εк входят одновременно в спектр А. Так как А*=А, то соответствующие собственные векторы ортогональны. Тогда имеет место разложение на собственные подпространства
), (к = 1,…, s). При этом операторы Р1 и Р2 неприводимы в Нφк (к = 1,…, s), и собственные значения 1+εк, 1-εк входят одновременно в спектр А. Так как А*=А, то соответствующие собственные векторы ортогональны. Тогда имеет место разложение на собственные подпространства
Нφк = Н1+εк ![]() Н1-εк , причем dimН1+εк = dimН1-εк = 1 (1.3)
Н1-εк , причем dimН1+εк = dimН1-εк = 1 (1.3)
Если φк ≠ φi, то εк ≠ εi (так как εк = ![]() =cosφк и φк
=cosφк и φк![]() (0,
(0, ![]() )). Объединим все Нφк , у которых одинаковые φк , в одно слагаемое, и обозначим его через Нφк. При этом, если dimНφк = 2qk, то есть Нφк состоит из qk экземпляров двумерных подпространств, отвечающих одному φк , то объединяя вместе все соответствующие одномерные собственные подпространства, получим Нφк = Н1+εк
)). Объединим все Нφк , у которых одинаковые φк , в одно слагаемое, и обозначим его через Нφк. При этом, если dimНφк = 2qk, то есть Нφк состоит из qk экземпляров двумерных подпространств, отвечающих одному φк , то объединяя вместе все соответствующие одномерные собственные подпространства, получим Нφк = Н1+εк ![]() Н1-εк , dimН1+εк = dimН1-εк = qk.
Н1-εк , dimН1+εк = dimН1-εк = qk.
Теорема 1.2. Самосопряженный оператор А представим в виде суммы двух ортопроекторов А = Р1 и Р2 тогда и только тогда, когда
![]() (А)
(А) ![]() {0, 1, 2}
{0, 1, 2}![]() (
(![]() {1+ε , 1-ε}), 0<εк<1,
{1+ε , 1-ε}), 0<εк<1,
причем dimН1+εк = dimН1-εк к = 1,…, m.
Доказательство. Пусть А = Р1 и Р2, тогда его спектр был найден выше:
![]() (А)
(А) ![]() {0, 1, 2}
{0, 1, 2}![]() (
(![]() {1+ε , 1-ε}), где 0<εк<1для любого к = 1,…, m.
{1+ε , 1-ε}), где 0<εк<1для любого к = 1,…, m.
Обратно, пусть нам известен спектр оператора А и известно, что размерности соответствующих собственных подпространств совпадают, то есть
dimН1+εк = dimН1-εк . Существует единственное разложение Н в ортогональную сумму инвариантных подпространств ((1.1.) Глава II):
Н = Н(0)![]() Н(1)
Н(1) ![]() Н(2)
Н(2)![]() (
(![]() (С2
(С2![]() Нк)) (1.4.)
Нк)) (1.4.)
(1.4.) можно записать иначе
Н = Н(0)![]() Н(1)
Н(1) ![]() Н(2)
Н(2)![]() (
(![]() (С2
(С2![]() (Н1+εк
(Н1+εк ![]() Н1-εк ))) (1.5.)
Н1-εк ))) (1.5.)
Зададим ортопроекторы Р1 и Р2 следующим образом
P1 = PН2![]() (
(![]() (
(![]()
![]() Iк )) (1.6.)
Iк )) (1.6.)
Р2 = PН1 ![]() PН2
PН2 ![]() (
(![]()
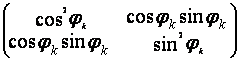
![]() Iк )) (1.7.)
Iк )) (1.7.)
где PНк – ортопроектор в Н на Н(к) (к = 1, 2), Is – единичный оператор в Hs s=1,…, m. Но тогда
Р1 + Р2 = PН1 ![]() PН2
PН2 ![]() (
(![]()
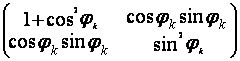
![]() Iк )) = А, при этом А = А*
Iк )) = А, при этом А = А*
1.6. Линейная комбинация ортопроекторов. Пусть теперь с. Из (1.2.) следует λ1 + λ2 = a + b. Пусть λ2 = ε, тогда λ1 = a + b – ε.
Оценим ε. Заметим, что (a +b)2 – 4ab(1-τ) = (a - b)2 + 4abτ > 0.
Тогда ε = 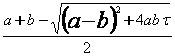 >
> 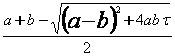 = 0, то есть ε = 0.
= 0, то есть ε = 0.
Допустим, что ε ≥ a , тогда
a ≤ 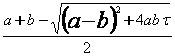
![]() ≤ b – a
≤ b – a
(b - a)2 +4abτ ≤ (b – a)2
abτ ≤ 0, но abτ > 0 и значит ε < a
Итак,
![]() λ1 = ε
λ1 = ε
λ2 = a + b – ε. (1.8.)
Похожие работы
... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...
... для того, чтобы показать школьникам образец современной математической теории. 2.2.3.2. ПРОГРАММА И СОДЕРЖАНИЕ ЗАНЯТИЙ ФАКУЛЬТАТИВНОГО КУРСА «ЭЛЕМЕНТЫ СОВРЕМЕННОЙ АЛГЕБРЫ» В качестве экспериментальной работы мы предлагаем изучение элементов современной алгебры в рамках факультативного курса по математике. Нами была разработана программа факультативного курса «Элементы современной алгебры» и ...
... угодно сложные в логическом отношении схемы, можно строить, используя два приема: 1. последовательное соединение элементов; 2. перестановка входов элементов. Этим двум физическим приемам в алгебре логики соответствуют: 1. принцип суперпозиции (подстановка в функцию вместо ее аргументов других функций); 2. подстановка аргументов (изменение порядка записи аргументов функций или замена ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...
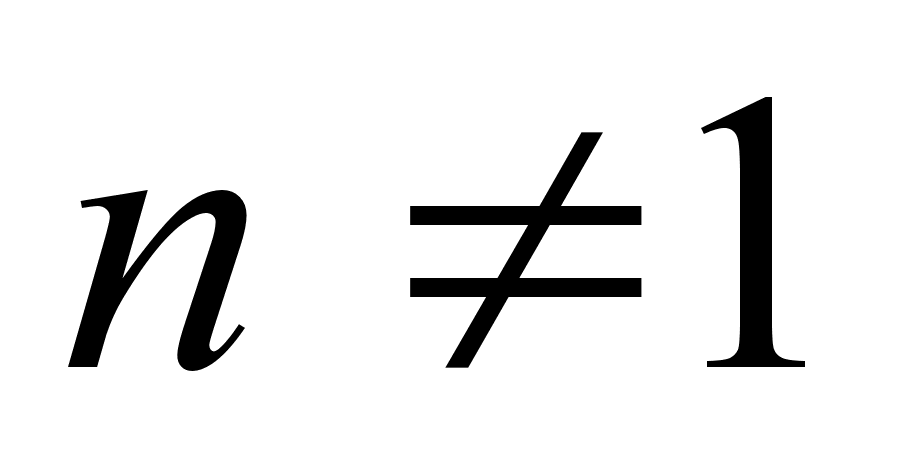

0 комментариев