Графический метод кинематического анализа
По свойству подобия находим на плане скоростей точку С, которая принадлежит звену 2 и 4, то есть является крайней точкой второй группы Ассура
Силовой анализ плоско-рычажного механизма
Определение уравновешивающей силы
Приведенный момент инерции рычажного механизма
Определение момента инерции маховика
Построение элементов зубчатого зацепления
Синтез редуктора с планетарной передачей
Навигация
По свойству подобия находим на плане скоростей точку С, которая принадлежит звену 2 и 4, то есть является крайней точкой второй группы Ассура
Анализ и синтез механизмов
27087
знаков
7
таблиц
13
изображений
4. По свойству подобия находим на плане скоростей точку С, которая принадлежит звену 2 и 4, то есть является крайней точкой второй группы Ассура.
Длину вектора 
определяем из соотношения:
откуда:
Отрезок 
представляет собой вектор скорости точки С.
5. Скорость средней точки второй группы Ассура D4 определяем через скорости крайних точек этой группы С и О3.
Скорость точки D4 относительно точки С:
Скорость точки D4 относительно точки О3:
Отрезок 
представляет собой вектор скорости точки D4, решаем графически.
Центры тяжести весомых звеньев определяем по свойству подобия.
6. Пользуясь планом скорости, определяем истинные (абсолютные) значения скоростей точек механизма:
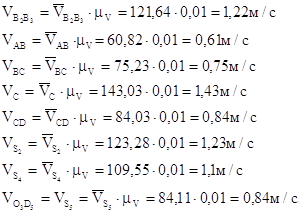
7. Определяем абсолютные величины угловых скоростей звеньев:
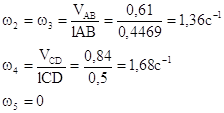
где lАВ= lАВ∙μl =89,38· 0,005 = 0,4469 м
1.2.2.2 Построение плана ускорения
Исходные данные: 1. Кинематическая схема механизма (1 лист)
2. Угловая скорость ведущего звена 
3. План скоростей для заданного положения.
1. Абсолютное ускорение точки А на конце ведущего звена:
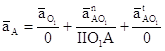
2. Масштабный коэффициент:
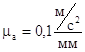
Длина вектора ускорения точки А1:
3. Ускорение средней точки первой группы Ассура – точки В2 определяем через ускорения крайних точек этой группы А и О2.
Ускорение точки В2 относительно точки А:
Ускорение точки В относительно точки О2:
Величина ускорения Кориолиса определяется по модулю формулой:
Длина вектора, изображающего ускорение Кориолиса на плане ускорений равна:
Для определения направления ускорения Кориолиса вектор относительной скорости 
поворачиваем на 90о по направлению угловой скорости 
.
Из конца вектора 
проводим линию действия релятивного ускорения 
параллельную звену АВ.
Решаем графически.
4. По свойству подобия находим на плане ускорения точку С, которая принадлежит звеньям 2 и 4, то есть является крайней точкой второй группы Ассура.
откуда:
5. Ускорение средней точки второй группы Ассура – точки D4 определяем через ускорения крайних точек этой группы C и О3, причем точка D4 принадлежит звену 4 и совпадает с точкой D5.
Ускорение точки D4 относительно точки С:
Ускорение точки D4 относительно точки О3:
Решаем графически.
Центры тяжести весомых звеньев определяем по свойству подобия
6. Пользуясь планом ускорений, определяем истинные (абсолютные) значения ускорений точек механизма:
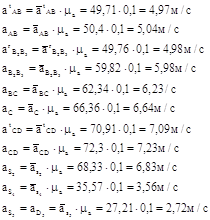
7. Определяем абсолютные величины угловых ускорений звеньев:
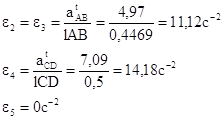
На этом кинематическое исследование кривошипно-ползунного механизма завершено.
Похожие работы
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... А. Черкудиновым (1959 г.), отразили состояние теории современного учения о механизмах. Одновременно И. И. Артоболевский начинает исследования в области теории механизмов машин автоматического действия: гидравлических, пневматических и гидропневматических. Для современных машин характерны вибрационные явления и существенное изменение массы в процессе работы. Чтобы учесть эти факторы, в большинстве ...
... успешному развитию у детей процессов пространственного анализа и синтеза. Заключение В данной работе были рассмотрены психологические условия коррекции нарушений пространственного анализа и синтеза у детей с психомоторными недостатками при помощи физических упражнений. В настоящее время внимание значительной части педагогов, психологов и социальных работников привлечено к ...
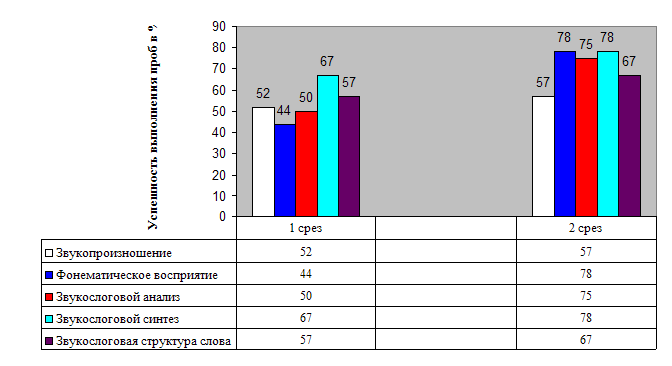
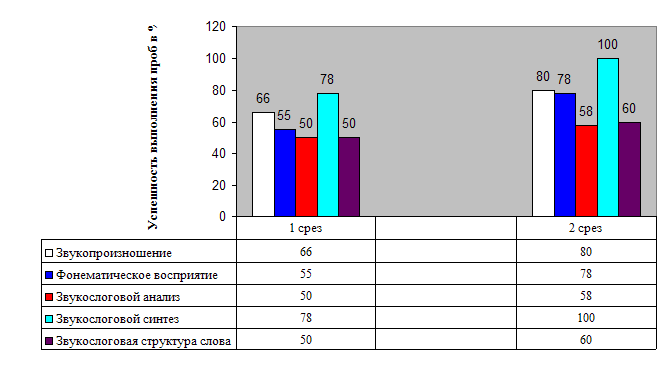
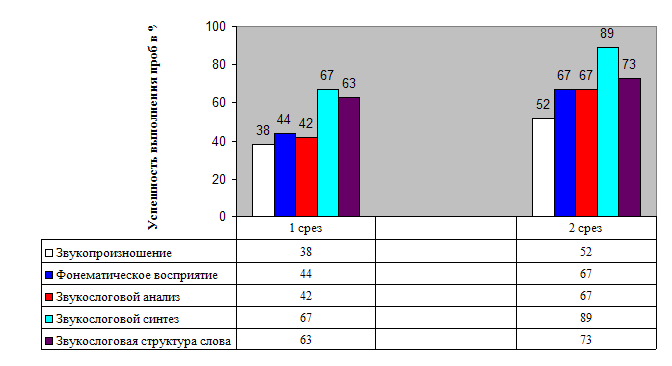
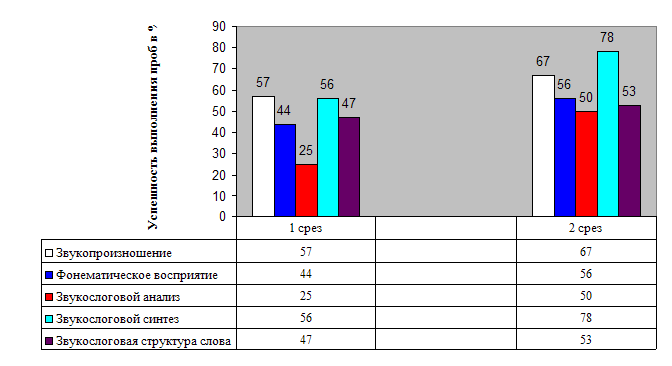
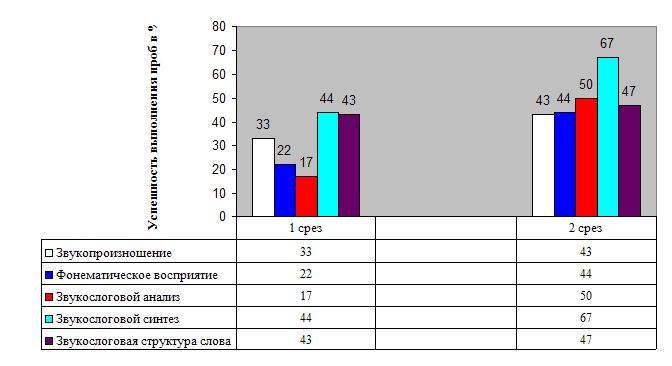
... находятся в слове. Для реализации основных направлений были подобраны специальные приемы и упражнения. Глава III ФОРМИРОВАНИЕ ЗВУКОСЛОГОВОГО АНАЛИЗА И СИНТЕЗА У МЛАДШИХ ШКОЛЬНИКОВ С ФОНЕТИКО-ФОНЕМАТИЧЕСКИМ НЕДОРАЗВИТИЕМ РЕЧИ 3.1 Динамика развития звукослогового анализа и синтеза у учащихся 1 класса После проведения серии коррекционно - развивающих занятий, был сделан второй контрольный ...
0 комментариев