Навигация
1.2 Розподіл Х²
Нехай 
(і=1,2,...,п)- нормальні незалежні випадкові величини, причому математичне чекання кожної з них дорівнює нулю, а середнє квадратичне відхилення - одиниці. Тоді сума квадратів цих величин
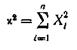
розподілена за законом Х² ("хи квадрат") з k=n ступенями волі; якщо ж ці величини зв'язані одним лінійним співвідношенням, наприклад 
, те число ступенів волі k=n-l. Диференціальна функція цього розподілу
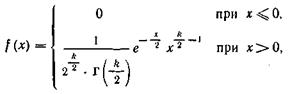
Де 
- гамма-функція; зокрема 
Звідси видно, що розподіл "хи квадрат" визначається одним параметром - числом ступенів волі k. Зі збільшенням числа ступенів волі розподіл повільний наближається до нормального.
1.3 Розподіл Стьюдента
Нехай Z - нормальна випадкова величина, причому M(Z)=0, cy(Z) - 1, а V - незалежна від Z величина, що розподілена за законом /2 з k ступенями волі.
Тоді величина
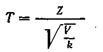
має розподіл, що називають t-розподілом, чи розподілом Стьюдента (псевдонім англійського статистика В. Госсета) з k ступенями волі.
Отже, відношення нормованої нормальної величини до квадратного кореня з незалежної випадкової величини, розподіленої за законом "хи квадрат" з k ступенями волі, діленої на k, розподілено за законом Стьюдента з k ступенями волі.
Зі зростанням числа ступенів волі розподіл Стьюдента швидко наближається до нормального. Додаткові зведення про цей розподіл приведені далі
1.4 Розподіл F Фішера-Снедекора
Якщо U і V незалежні випадкові величини, розподілені за законом х2 зі ступенями волі 
і 
, те величина
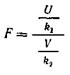
має розподіл, що називають розподілом F Фішера-Снедекора зі ступенями волі і (іноді його позначають через V²). Диференціальна функція
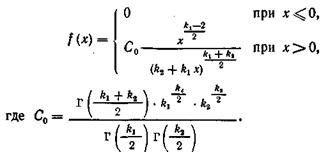
Ми бачимо, що розподіл F визначається двома параметрами - числами ступенів волі.
2. Емпірична функція розподілу
Нехай відомо статистичний розподіл частот кількісної ознаки X. Введемо значення п х — число спостережень, менше х; п — загальне число спостережень (об’єм вибірки). Ясно, що відносна частота події X <1 дорівнює n(x)/п. Якщо х змінюється, то, взагалі говорячи, змінюється і відносна частота, тобто відносна частота пх /п є функція від х. Тому що ця функція знаходиться емпіричним (досвідченим) шляхом, то її називають емпіричною.
Емпіричною функцією розподілу (функцією розподілу вибірки) називають функцію F*(x), що визначає для кожного значення х відносну частоту випадку X < х. '
Отже, по визначенню:
F(x)=nx/n
Де nx-число варіант, менших х; п — об'єм вибірки. Таким чином, для того щоб знайти, наприклад, F*(xi), потрібно число варіант, менших хг, розділити на об’єм вибірки: F*(x2) = nx2/n.
На відміну від емпіричної функції розподілу вибірки функцію розподілу F (х) генеральної сукупності називають теоретичною функцією розподілу. Різниця між емпіричної і теоретичної функціями полягає в тому, що теоретична функція F (х) визначає імовірність події X < х, а емпірична функція F* (х) визначає відносну частоту події. З теореми Бернуллі випливає, що відносна частота події X < х, тобто F* (х) прагне по імовірності до імовірності F (х) цієї події. Іншими словами, при великих п числа F* (х) і F (х) мало відрізняються одне від іншого в тому змісті, що lim n-¥Р [ | F (х)- F* (х) | < е] = 1 (е > 0). Уже звідси випливає доцільність використання емпіричної функції розподілу вибірки для наближеного представлення теоретичної (інтегральної) функції розподілу генеральної сукупності.
Такий висновок підтверджується і тим, що F*(x) наділене усіма властивостями F (х). Дійсно, з визначення функції F* (х) випливають наступні її властивості: 1) значення емпіричної функції належать відрізку [О, 1];
2) F*(x) — функція, що не спадає;
3) якщо Xi — найменша варіанта, то F*(x) = Q при x
x1; якщо xk—найбільша варіанта, то F* (х) = 1 при x> xk.
Отже, емпірична функція розподілу вибірки служить для оцінки теоретичної функції розподілу генеральної сукупності.
Приклад.
Побудувати емпіричну функцію по даному розподілу вибірки:
варіанти xi 2 6 10
частоти ni 12 18 30
Розв’язок. Знайдемо обсяг вибірки: 12 + 18 + 30 = 60. Найменша варіанта дорівнює 2, отже,
F*(x) = О при x2. І
Значення X < 6, а саме x1 = 2, спостерігалося 12 разів, отже,
:F*(x) = 12/60 = 0,2 при
2<x6. I
значення x<10, а саме x1 = 2 і х2 = 6, спостерігалися 12 + 18 = 30 разів, отже,
F* (х) = 30/60 = 0,5 при 6 < х 10. Тому що x=10 — найбільша варіанта, то | F*(x)=1 при х > 10. Шукана емпірична функція
Графік цієї функції зображений на малюнку.
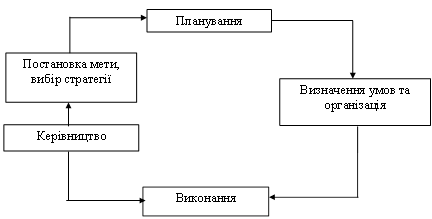
3. Точечні та інтервальні оцінки параметрів розподілу
3.1 Точечна оцінка параметрів розподілу
Є два підходи до оцінювання невідомих параметрів розподілів по спостереженнях: точечний і інтервальний. Точечний вказує лише точку, біля якої знаходиться оцінюваний параметр; при інтервальному знаходять інтервал, що з деякою великою ймовірністю, що задається дослідником, накриває невідоме числове значення параметра. У главі розглядаються методи точечного оцінювання параметрів; будуються інтервальні оцінки параметрів нормального розподілу, обговорюється загальний підхід до інтервального оцінювання параметрів розподілу, відмінних від нормального.
Похожие работы
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... поданих на рис. 1.5 методик. Відповідно до цієї методики аналіз інвестиційної привабливості підприємства здійснюється в послідовності, наведеній на рис. 1.6. Аналіз і оцінка інвестиційної привабливості підприємства на основі аналізу фінансових показників передбачають дослідження фінансово-економічних процесів на підприємстві (табл. 1.2). Таблиця 1.2 Цілі аналізу фінансово-економічних процесів ...
... і невилучених систематичних складових повної похибки результату вимірювання, її оцінювання проводиться відповідно до методики, викладеної в підп.2.9.4. Оцінка результату і похибки прямих багаторазових вимірювань Постійно зростаючі вимоги до точності прямих вимірювань задовольняються не тільки за рахунок підвищення точності заново створених ЗВТ, але й використанням більш ефективних методів ...
... заційної реструктуризації. Щоб більш результативно запобігати банкрутству, необхідно вирішити завдання запровадження ефективних, адаптованих до вітчизняних умов, механізмів визначення ймовірності банкрутства ще до виникнення явних ознак неплатоспроможності підприємства, а також створити відповідну систему моніторингу роботи підприємств на рівні регіонів. Аналіз літератури показує, що у даний час ...
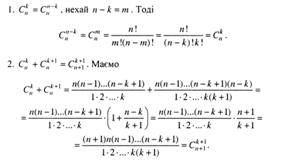
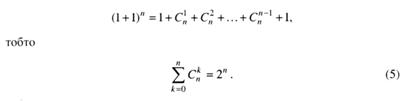
0 комментариев