Навигация
Відповідно до рівняння (3.2.21)
39861
знак
0
таблиц
10
изображений
2. Відповідно до рівняння (3.2.21),
а так як при k = п -1 = 18 50, 
= 0,297 (див. табл. П. 4.6), то 17,575<σ<32,425 - ця оцінка симетрична щодо s. Вона, як і випливало очікувати, відрізняється від попередньої інтервальної оцінки, однак 
3.2.1 Асимптотичний підхід до інтервального оцінювання
З прикладами інтервальних оцінок, що мають місце тільки при великих об'ємах вибірок, ми вже зштовхувалися. Так, якщо розподіл випадкового розміру X відмінно від нормального, але п велике, то з імовірністю ≈ 1 - а інтервальна оцінка для MX = а має вид нерівності (3.2.3); з імовірністю ≈ 1-а інтервальна оцінка для р при великих п має вид нерівності (3.2.6) і т. д. [див. нерівності (3.2.9), (3.2.23)].
Розглянемо асимптотичний підхід у загальному випадку.
Раніше було встановлено, що при виконанні досить широких умов оцінка 
параметра 
, отримана або методом моментів або методом максимальної правдоподібності, має в самому загальному випадку асимптотичний нормальний розподіл і асимптотично несумісної, тобто при великих п оцінка 
. Однак на відміну від ситуації, розглянутої на раніше, де дисперсія D
оцінки 
передбачалася відомої, у загальному випадку дисперсія Dоцінки залежить від оцінюваного невідомого параметра θ:
(3.2.24)
Тому напряму перший підхід до довірчого інтервалу неприйнятий.
Порушимо питання так: не можна чи перетворити оцінку 
у g – g() це невідомий параметр у g = g (θ) так, щоб дисперсія D
не залежала від θ. Викладемо схему добору такого перетворення, а потім пояснимо, як, використовуючи його, знайти інтервальну оцінку для θ.
Нехай θ — оцінка методу моментів: θ, а отже, і g = g(θ) є функціями вибіркових моментів. Тоді, відповідно до теореми про властивості функцій вибіркових моментів (див. 3.1), розподіл оцінки 
при великих п близько до нормального, 
і, з обліком виражень (3.5) і (3.2.25),
(аналогічні вираження утворюються і для оцінок максимальної правдоподібності в регулярному випадку). Але тому що дисперсія Dне повинна залежати від θ, то вираження c(θ) g'(θ) повинно бути постійним, наприклад, c(θ)g'(θ) = 1. Тоді g'(θ)= 1/ c(θ) і
(3.2.25)
при цьому довільна постійна в невизначеному інтегралі вибирається з розумінь простоти остаточних виражень.
Отже, при великих п розподіл оцінки близько до нормального, при цьому 
, a 
і, отже,
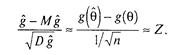
Тому при великих п для g(9) з імовірністю * I — а має місце нерівність, подібна нерівності (3.2.3):
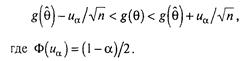(3.2.26)
Застосувавши до всіх частинам нерівності (3.2.26) перетворений не 
, що є зворотною функцією до функції g, одержимо інтервальну оцінку для θ.
Приклад 3.2.5 Побудуємо довірчий інтервал для параметра розподілення Пуассона: Р(Х = х) =
л.
У прикладі 3.2.2 була знайдена оцінка методу моментів 
параметра 
; 
будучи оцінкою методу моментів, має асимптотично нормальний розподіл (ця властивість оцінки 
випливає також і з центральної граничної теореми), при цьому - оцінка, тому що 
, а дисперсія оцінки , залежить від параметра λ:
Зіставивши вираження для 
с вираженням (3.2.24), одержимо 
і, відповідно до рівності (3.2.25),
З урахуванням виду функції 
нерівність (3.2.26)
(3.2.27)
Для функції 
при х ≥ 0 і у ≥ 0 зворотна функція 
. Тому, якщо в нерівності (3.2.27)
то, застосувавши до всіх його частинам перетворення одержимо нерівність
(3.2.28)
яке виконується при великих п з імовірністю ≈ 1 - α.
Приклад 3.2.6 Побудуємо довірчий інтервал для р - імовірності успіху в одиничному випробуванні.
У прикладі 3.2.4 методом максимальної правдоподібності для р була знайдена оцінка 
, де 
- випадкове число успіхів у п випробуваннях Бернуллі; р має асимптотичний нормальний розподіл, при цьому М
= р, a D= р(1 – р)/п - дисперсія залежить від параметра р.
Зіставивши вираження для D із вираженням (3.2.24), одержимо
і, відповідно до формули (3.2.25),
З обліком виду функції g(p) нерівність (3.2.26) прийме вид:
(3.2.29)
Для функції 
при 0 < 
< 1 зворотна функція 
, де 0 < у < π. Тому, якщо в нерівності (3.2.29)
та 
, то застосувавши до всіх його частинам перетворення одержимо нерівність;
який виконується при великих п з імовірністю ≈ 1 - α.
Похожие работы
... . Поклавши у формулі (4) а = b = 1, дістанемо Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}. ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ § 1. Про предмет теорії ймовірностей До цього часу розглядалися задачі, в яких результат дії був однозначно ...
... поданих на рис. 1.5 методик. Відповідно до цієї методики аналіз інвестиційної привабливості підприємства здійснюється в послідовності, наведеній на рис. 1.6. Аналіз і оцінка інвестиційної привабливості підприємства на основі аналізу фінансових показників передбачають дослідження фінансово-економічних процесів на підприємстві (табл. 1.2). Таблиця 1.2 Цілі аналізу фінансово-економічних процесів ...
... і невилучених систематичних складових повної похибки результату вимірювання, її оцінювання проводиться відповідно до методики, викладеної в підп.2.9.4. Оцінка результату і похибки прямих багаторазових вимірювань Постійно зростаючі вимоги до точності прямих вимірювань задовольняються не тільки за рахунок підвищення точності заново створених ЗВТ, але й використанням більш ефективних методів ...
... заційної реструктуризації. Щоб більш результативно запобігати банкрутству, необхідно вирішити завдання запровадження ефективних, адаптованих до вітчизняних умов, механізмів визначення ймовірності банкрутства ще до виникнення явних ознак неплатоспроможності підприємства, а також створити відповідну систему моніторингу роботи підприємств на рівні регіонів. Аналіз літератури показує, що у даний час ...
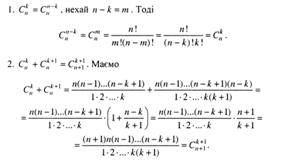
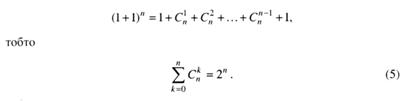
0 комментариев