Навигация
Знайти всі значення а, при яких система має єдиний розв’язок
2. Знайти всі значення а, при яких система має єдиний розв’язок.
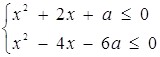
Розв’язок. Перепишемо початкову систему в такому вигляді:
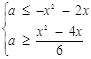
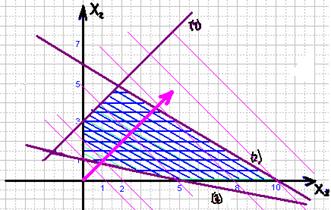
Все розв’язки цієї системи (пари виду![]() ) утворюють область, наведену на рис.2.8 штриховою лінією.
) утворюють область, наведену на рис.2.8 штриховою лінією.
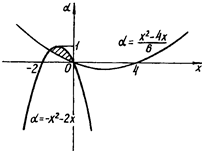
Рис.2.8
Вимога єдності розв’язка даної системи така: горизонтальні прямі повинні мати зі знайденою областю тільки одну спільну точку. Лише прямі а = 0 та а = 1 задовольняють висунутій вимозі.
Відповідь: а = 0 або а = 1.
3. При яких значеннях а рівняння ![]() має
має
рівно три кореня?
Розв’язок. Маємо
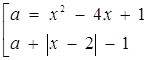
Графік цієї сукупності - об’єднання "кута" та параболи (рис.2.9).
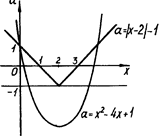
Рис.2.9
Лише пряма ![]() перетинає знайдене об’єднання в трьох точках.
перетинає знайдене об’єднання в трьох точках.
Відповідь: ![]()
4. Скільки розв’язків має система в залежності від значень параметра с?
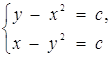
Розв’язок. Перепишемо систему у вигляді
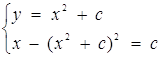
Кількість коренів другого рівняння системи дорівнює числу розв’язків самої системи. Маємо ![]() . Розглянувши це рівняння як квадратне відносно с, одержимо наступну сукупність.
. Розглянувши це рівняння як квадратне відносно с, одержимо наступну сукупність.
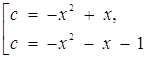
На рис.2.10 наведено сукупність рівнянь на координатній площині ![]() .
.
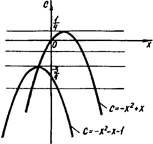
Рис.2.10
Координати точок перетину парабол можна знайти, розв’язавши рівняння ![]() . Звідси
. Звідси ![]() . Для запису відповіді залишилося лише зазначити, що спільна точка цих парабол - вершина параболи
. Для запису відповіді залишилося лише зазначити, що спільна точка цих парабол - вершина параболи ![]() .
.
Відповідь: якщо ![]() , то розв’язків чотири; якщо
, то розв’язків чотири; якщо ![]() , то
, то
розв’язків два; якщо ![]() , то розв’язок один; якщо
, то розв’язок один; якщо ![]() , то розв’язків немає.
, то розв’язків немає.
5. Знайти всі значення параметра b, при яких рівняння ![]() має один розв’язок.
має один розв’язок.
Розв’язок. Задане рівняння рівносильне системі
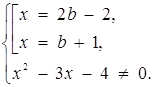
За допомогою цієї системи будуємо графік початкового рівняння (рис.2.11).

Рис.2.11
Саме наявність "проколов" в цьому графіку дозволяє при ![]() та
та ![]() мати рівнянню єдиний розв’язок.
мати рівнянню єдиний розв’язок.
Відповідь: ![]() або
або ![]()
6. При яких значеннях параметра а рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язок. Запишемо систему, рівносильну початковому рівнянню:
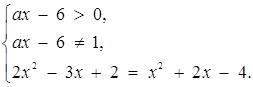 , Звідси знайдемо
, Звідси знайдемо
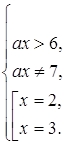
Перші дві нерівності системи задають множину точок, наведену на рис.2.12 штриховою лінією, причому в цю множину не входять гіперболи ах = 7 та ах = 6.
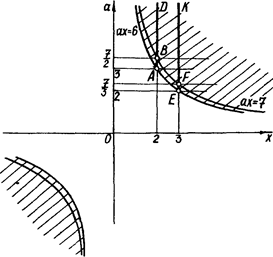
Рис.2.12
Тоді відрізок АВ та промінь BD, відрізок EF та промінь FK, які лежать відповідно на прямих ![]() та
та ![]() , є графіком початкового рівняння. Далі залишилося лише "зняти" з картинки:
, є графіком початкового рівняння. Далі залишилося лише "зняти" з картинки: ![]() або
або ![]() або
або ![]()
Відповідь: ![]() або
або ![]() або
або ![]()
7. Знайти всі значення параметра а, при яких рівняння ![]() має рівно два різних розв’язки.
має рівно два різних розв’язки.
Розв’язок. Задане рівняння рівносильне сукупності двох систем:
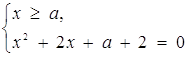 або
або 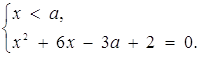 Звідси
Звідси
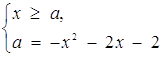 або
або 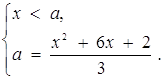
При побудови графіка початкового рівняння важливо врахувати, що параболи ![]()
![]() та пряма
та пряма ![]() мають дві спільні точки: А (-2; - 2), В (-1; - 1), причому точка В - вершина першої з записаних парабол. Вершина другої параболи
мають дві спільні точки: А (-2; - 2), В (-1; - 1), причому точка В - вершина першої з записаних парабол. Вершина другої параболи ![]()
Графік початкового рівняння наведено на рис.2.13.
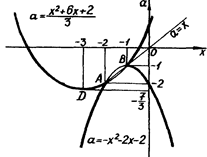
Рис.2.13
Звідси знаходимо ![]() або
або ![]() . Відповідь:
. Відповідь: ![]() або
або ![]() .
.
8. Знайти множину всіх чисел а, для кожного з яких рівняння ![]() має тільки два різних кореня.
має тільки два різних кореня.
Розв’язок. Перепишемо задане рівняння в наступному виді: ![]() Тепер важливо не втратите, що
Тепер важливо не втратите, що ![]()
![]() та
та ![]() - корені початкового рівняння лише при умові
- корені початкового рівняння лише при умові ![]() Графік заданого рівняння зручно будувати, відводячи змінній х вісь ординат. На рис.2.14 шуканий графік - об’єднання неперервних ліній.
Графік заданого рівняння зручно будувати, відводячи змінній х вісь ординат. На рис.2.14 шуканий графік - об’єднання неперервних ліній.
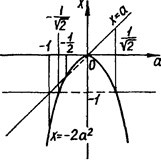
Рис.2.14
Відповідь "зчитується" вертикальними прямими: ![]() або
або ![]() або
або ![]()
Відповідь: ![]() або
або ![]() або
або ![]()
9. Знайти всі невід’ємні числа ![]() при яких існує єдине число
при яких існує єдине число ![]() яке задовольняє системі
яке задовольняє системі
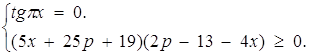
Розв’язок. Маємо
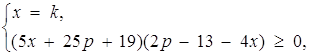 де
де ![]()
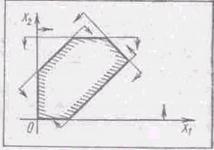
Перше рівняння на координатній площині ![]() задає сім’ю вертикальних прямих (рис.2.15). Прямі
задає сім’ю вертикальних прямих (рис.2.15). Прямі ![]() та
та ![]() розбивають площину на чотири області. Деякі з них є розв’язками нерівності системи. Для того, щоб встановити які - можна взяти з кожної області по пробній точці. Та область, точка якої задовольняє нерівності, є її розв’язком. Для заданої нерівності розв’язком будуть дві області, обмежені кутами АМВ та DMC. Оскільки за умовою
розбивають площину на чотири області. Деякі з них є розв’язками нерівності системи. Для того, щоб встановити які - можна взяти з кожної області по пробній точці. Та область, точка якої задовольняє нерівності, є її розв’язком. Для заданої нерівності розв’язком будуть дві області, обмежені кутами АМВ та DMC. Оскільки за умовою ![]() то для розв’язку задачі достатньо обмежитися множиною, відміченою штриховою лінією на рис.2.15.
то для розв’язку задачі достатньо обмежитися множиною, відміченою штриховою лінією на рис.2.15.
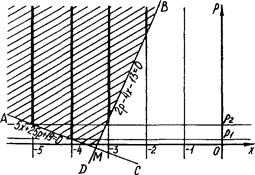
Рис.2.15
Тоді початковій системі задовольняють всі точки (і тільки вони), які лежать на променях і виділені на графіку жирними лініями.
При фіксованому ![]() число розв’язків початкової системи дорівнює кількості точок перетину горизонтальної прямої
число розв’язків початкової системи дорівнює кількості точок перетину горизонтальної прямої ![]() з відміченими променями. По рисунку видно, що вимога єдиності розв’язку досягається, якщо
з відміченими променями. По рисунку видно, що вимога єдиності розв’язку досягається, якщо ![]() , де
, де ![]() та
та ![]() - відповідно ординати точок перетину двох пар прямих
- відповідно ординати точок перетину двох пар прямих ![]()
![]() та
та ![]()
![]() Звідси
Звідси ![]()
![]()
Відповідь: ![]()
10. Для яких а в множині розв’язків нерівності ![]() міститься проміжок
міститься проміжок ![]() ?
?
Розв’язок. Запишемо сукупність двох систем, рівносильну початковому рівнянню:
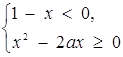 або
або 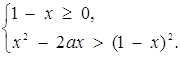
Оскільки в розв’язок першої системи ні при яких значеннях параметра а не може входити відрізок ![]() , то необхідні дослідження проведемо для другої системи. Маємо
, то необхідні дослідження проведемо для другої системи. Маємо
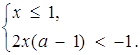
Позначимо ![]() Тоді друга нерівність системи на координатній площині
Тоді друга нерівність системи на координатній площині ![]() задає множину, наведену на рис.2.16 штриховою лінією.
задає множину, наведену на рис.2.16 штриховою лінією.
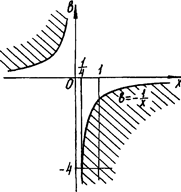
Рис.2.16
Тепер за допомогою рисунка легко встановити, що при ![]() в знайденій множині містяться всі точки, абсциси яких пробігають всі значення з проміжку
в знайденій множині містяться всі точки, абсциси яких пробігають всі значення з проміжку ![]() Тоді
Тоді ![]() Звідси
Звідси ![]()
Відповідь: ![]()
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
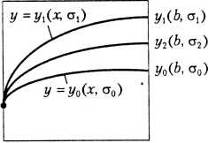
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
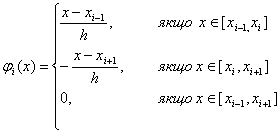

0 комментариев