Навигация
Знайти всі а, при яких системи рівносильні
4. Знайти всі а, при яких системи рівносильні.
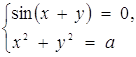 та
та 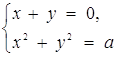
Розв’язання. Перепишемо першу систему в виді 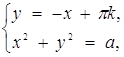 де
де ![]()
Перше рівняння системи задає сім’ю паралельних прямих, зображену на рис.1.3.12. Для випадку а > 0 друге рівняння системи задає сім’ю кіл.
Всі розв’язки другої з початкових систем містяться серед розв’язків першої.
Обернена вимога виконується лише тоді, коли кола ![]() мають спільні точки тільки з прямою
мають спільні точки тільки з прямою ![]() . Відстань між сусідніми прямими дорівнює
. Відстань між сусідніми прямими дорівнює ![]() , тому для радіуса кола знаходимо обмеження
, тому для радіуса кола знаходимо обмеження ![]() . Звідси
. Звідси ![]() .
.

Рис.1.3.12
Оскільки ми розглядаємо випадок а > 0, то значення а = 0 потребує перевірки. Очевидно воно підходить. При а < 0 початкові системи розв’язків не мають, а значить, вони рівносильні.
Відповідь: ![]() .
.
5. При яких додатних значеннях параметрів а та ![]() системи рівнянь
системи рівнянь
 та
та 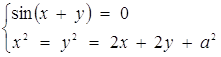
мають однакове число розв’язків?
Розв’язання. Друга система задає сім’ю паралельних прямих ![]() , та сім’ю гомотетичних кіл
, та сім’ю гомотетичних кіл ![]() з центром О1 (1;
з центром О1 (1;
1) (рис.1.3.13). Оскільки за умовою ![]() , то
, то ![]() , і система має не менше чотирьох розв’язків. Очевидно такою ж властивістю володіє перша з початкових систем.
, і система має не менше чотирьох розв’язків. Очевидно такою ж властивістю володіє перша з початкових систем.
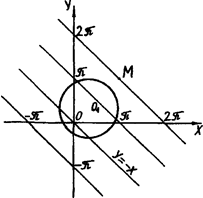
Рис.1.3.13
Вона рівносильна сукупності наступних двох систем:
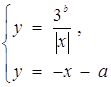 або
або 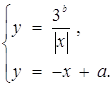
Оскільки а > 0, то сім’я паралельних прямих ![]() (рис.1.3.13) перетинає графік
(рис.1.3.13) перетинає графік  лише в одній точці, а значить, перша система сукупності має тільки один розв’язок. Друга система може мати не більше трьох розв’язків (рис.1.3.14). Тому ми вимагаємо від цієї системи мати рівно три розв’язки.
лише в одній точці, а значить, перша система сукупності має тільки один розв’язок. Друга система може мати не більше трьох розв’язків (рис.1.3.14). Тому ми вимагаємо від цієї системи мати рівно три розв’язки.

Рис.1.3.14
Остання умова досягається тоді, коли прямі ![]() будуть перетинати криву
будуть перетинати криву ![]() , в двох точках. Для цього необхідно і достатньо, щоб рівняння
, в двох точках. Для цього необхідно і достатньо, щоб рівняння ![]() при а > 0 мало два кореня, тобто дискримінант квадратного рівняння
при а > 0 мало два кореня, тобто дискримінант квадратного рівняння ![]() повинен бути додатним. Маємо
повинен бути додатним. Маємо ![]() . Звідси для а > 0 знаходимо
. Звідси для а > 0 знаходимо ![]()
Тепер залишилося з’ясувати, при яких а друга з даних в умові систем має рівно чотири розв’язки. Розглянемо точку ![]() (рис.1.3.13). Якщо радіус кола буде більше або дорівнює О1М, то система очевидно буде мати більше чотирьох розв’язків. Тоді знаходимо
(рис.1.3.13). Якщо радіус кола буде більше або дорівнює О1М, то система очевидно буде мати більше чотирьох розв’язків. Тоді знаходимо ![]() , тобто при а > 0 маємо
, тобто при а > 0 маємо ![]() .
.
Тепер визначимо при яких ![]()
![]() . Легко встановлюємо, що
. Легко встановлюємо, що ![]() .
.
Відповідь: якщо ![]() , то
, то ![]() ; при інших b вимоги задачі не виконуються.
; при інших b вимоги задачі не виконуються.
Зауваження. При фіксованому ![]() крива
крива ![]() - результат стиску до вісі абсцис кривої
- результат стиску до вісі абсцис кривої ![]() в
в ![]() раз. (Іноді для випадку
раз. (Іноді для випадку ![]() говорять, що крива розтягується від вісі)
говорять, що крива розтягується від вісі)
6. При кожному фіксованому значенні параметра а розв’язати рівняння ![]() .
.
Розв’язання. Розглянемо функції ![]() и
и ![]() . На рис.1.3.15 побудовані графік першої з них, а також графіки шести представників сім’ї прямих
. На рис.1.3.15 побудовані графік першої з них, а також графіки шести представників сім’ї прямих ![]() відповідно для випадків
відповідно для випадків ![]()
![]()
![]()
![]()
![]()
![]() (Для а = 0 маємо вісь абсцис) Одержаний графічний образ дає повну інформацію про Розв’язання початкового рівняння. Залишилося лише знайти значення
(Для а = 0 маємо вісь абсцис) Одержаний графічний образ дає повну інформацію про Розв’язання початкового рівняння. Залишилося лише знайти значення ![]() та
та ![]() .
.

Рис.1.3.15
Очевидно шукані значення відповідно для ![]() и
и ![]() - це корені рівняння
- це корені рівняння ![]() .
.
Звідси ![]() . При запису відповіді необхідно врахувати, що х = 1 - корінь початкового рівняння при будь-якому а.
. При запису відповіді необхідно врахувати, що х = 1 - корінь початкового рівняння при будь-якому а.
Відповідь: якщо ![]() , то х = 1; якщо
, то х = 1; якщо ![]() , то х = 1 або
, то х = 1 або ![]() ;
;
якщо а = 1, то ![]() ; якщо а = - 1, то
; якщо а = - 1, то ![]() .
.
7. Знайти всі натуральні значення b, при кожному з яких вираз 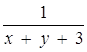 має зміст для всіх пар чисел (х; у), де
має зміст для всіх пар чисел (х; у), де ![]() и
и ![]() , для яких вираз
, для яких вираз![]() також має зміст.
також має зміст.
Розв’язання. Оскільки вирази 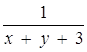 та
та ![]() повинні мати зміст одночасно, то нескладно прийти до формулювання, рівносильного початковому: знайти всі натуральні b, при яких система має розв’язок:
повинні мати зміст одночасно, то нескладно прийти до формулювання, рівносильного початковому: знайти всі натуральні b, при яких система має розв’язок:
Графіком першої нерівності системи є всі точки координатної площини (х; у), окрім прямої ![]() . Інші нерівності задають область, обмежену віткою гіперболи
. Інші нерівності задають область, обмежену віткою гіперболи ![]() . (На рис.1.3.16 ця область показана штриховою лінією)
. (На рис.1.3.16 ця область показана штриховою лінією)
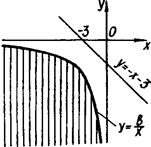
Рис.1.3.16
Система має розв’язки, якщо сім’я гіпербол ![]() має не більше однієї спільної точки з прямою
має не більше однієї спільної точки з прямою ![]() (одна точка відповідає моменту дотику). Для цього достатньо вимагати, щоб рівняння
(одна точка відповідає моменту дотику). Для цього достатньо вимагати, щоб рівняння ![]() мало не більше одного кореня. Оскільки
мало не більше одного кореня. Оскільки ![]() , то умова недодатності дискримінанта квадратного рівняння
, то умова недодатності дискримінанта квадратного рівняння ![]() дає шукані значення параметра. Маємо
дає шукані значення параметра. Маємо ![]() . І так як b - натуральне, знаходимо b=3, 4,...
. І так як b - натуральне, знаходимо b=3, 4,...
Відповідь: b=3, 4,...
8. При яких значеннях а множина точок, задана нерівністю ![]() , є підмножиною множини точок, заданої нерівністю
, є підмножиною множини точок, заданої нерівністю ![]() ?
?
Розв’язання. Графіком нерівності ![]() є область, обмежена ромбом (рис.1.3.17).
є область, обмежена ромбом (рис.1.3.17).
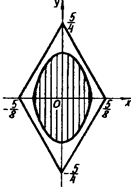
Рис.1.3.17
Нерівність ![]() рівносильна системі
рівносильна системі ![]() . Очевидно при
. Очевидно при ![]() ця система задає необмежену множину точок (рис.1.3.18), яка не може поміститися в середині ромба. Якщо а > 0, то система задає фігуру, зображену на рис.1.3.19.
ця система задає необмежену множину точок (рис.1.3.18), яка не може поміститися в середині ромба. Якщо а > 0, то система задає фігуру, зображену на рис.1.3.19.
Задача зводиться до пошуку значень а, при яких ця фігура "стиснеться" до таких розмірів, що поміститься в ромб. Із міркувань симетрії для пошуку шуканих значень параметра достатньо вимагати від рівняння ![]() при
при ![]() мати не більше одного кореня. Тоді
мати не більше одного кореня. Тоді ![]() .
.
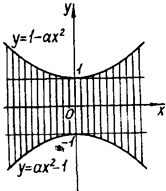
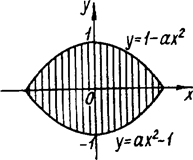
Рис.1.3.18 Рис.1.3.19
Відповідь: ![]() .
.
1.4 Дві прямі на площині
В основі ідеї розв’язку задач цього підрозділу лежить питання про дослідження взаємного розташування двох прямих: ![]() та
та ![]() . Не будь-яке рівняння виду
. Не будь-яке рівняння виду ![]() задає пряму: необхідно ще вимагати, щоб
задає пряму: необхідно ще вимагати, щоб ![]() При дослідженні взаємного розташування двох прямих зручно спочатку розглянути випадки, коли коефіцієнти при у дорівнюють нулю (маємо вертикальне положення прямих), потім кожне з рівнянь представити у вигляді
При дослідженні взаємного розташування двох прямих зручно спочатку розглянути випадки, коли коефіцієнти при у дорівнюють нулю (маємо вертикальне положення прямих), потім кожне з рівнянь представити у вигляді ![]()
1. Знайти значення ![]() , при яких система рівнянь
, при яких система рівнянь
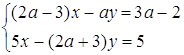
має єдиний розв’язок.
Розв’язання. Графіками рівнянь системи є прямі. Перше рівняння при ![]() задає вертикальну пряму
задає вертикальну пряму ![]() , яка перетинає графік другого рівняння, що рівносильно для системи мати єдиний розв’язок. Друге рівняння при
, яка перетинає графік другого рівняння, що рівносильно для системи мати єдиний розв’язок. Друге рівняння при ![]() задає вертикальну пряму
задає вертикальну пряму ![]() , яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
, яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо ![]() та
та ![]() , то
, то ![]() ,
, ![]() .
.
Прямі паралельні, якщо 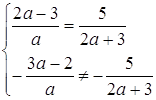 , звідки
, звідки ![]()
Прямі співпадають, якщо 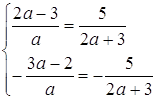 , звідки
, звідки ![]()
Прямі перетинаються, якщо ![]() , звідки
, звідки ![]() .
.
Відповідь: система має єдиний розв’язок при ![]() .
.
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
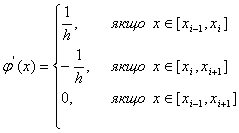
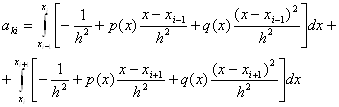
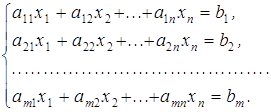
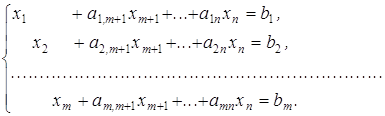
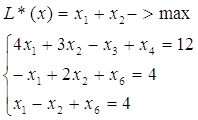
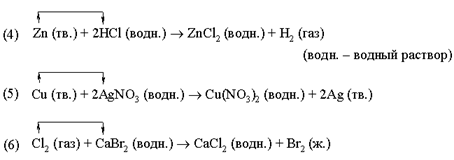

0 комментариев