При яких значеннях параметра а система

11. При яких значеннях параметра а система

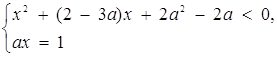
має розв’язки?

Розв’язок. Маємо

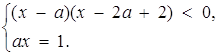
Нерівність системи задає область, обмежену кутами АКБ и CKD (рис.2.17).

.

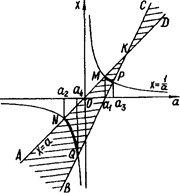
Рис.2.17

Тоді абсциси виділених дуг гіперболи  - розв’язки початкової системи. Знайдемо абсциси точок  розв’язавши рівняння  та Звідси для перелічених точок абсциси відповідно дорівнюють   Залишилося записати  або

Відповідь:  або

12. Знайти всі значення а, при яких будь-який розв’язок нерівності  по модулю, не перевищує двох.

Розв’язок. Перепишемо задану нерівність в такому виді:

Графіки рівнянь  и  розбивають координатну площину  на чотири області. "Методом інтервалів" встановлюємо, що розв’язком початкової нерівності будуть заштриховані області (рис.2.18).

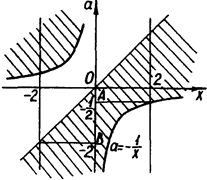
Рис.2.18

Тепер, якщо при деякому фіксованому значенні  пряма  в перетині зі знайденою областю дає лише точки, абсциси яких задовольняють умові  то  - одне з шуканих значень параметра. Тоді очевидно, що всі а з відрізка АВ складаються

Відповідь:

13. При яких значеннях а множина розв’язків нерівності  містить не більше чотирьох цілих значень ?

Розв’язок. Раніше встановлено, що задана нерівність рівносильна сукупності двох систем:

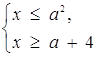 або

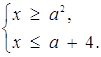
За допомогою цієї сукупності наведено розв’язки початкової нерівності на рис.2.19.

Рис.2.19

Проведемо прямі  де  Тоді значення  для якого пряма  перетинає прямі  не більш, ніж в чотирьох точках з відміченої множини, буде шуканим. Проводячи аналіз графіка, приходимо до висновку, що в заданій задачі  або  або

Відповідь:  або  або

14. Розв’язати нерівність.

Розв’язок. Наступна сукупність двох систем рівносильна заданій нерівності:

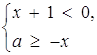 або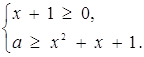

Далі, при об’єднанні графічних образів кожної з цих систем необхідно врахувати, що пряма  дотикається параболи  в точці (-1;1).

На рис.2.20 наведено всі розв’язки початкової нерівності.

Горизонтальні прямі, які перетинають цю множину, перетинають її по відрізку (за виключенням однієї прямої ). Очевидно абсциси всіх точок цього відрізка і будуть розв’язками заданої нерівності.

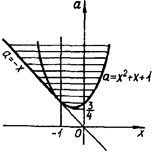
Рис.2.20

Для одержання відповіді залишилося виразити х через а в рівнянні  При  маємо

Відповідь: при  розв’язків не має; при  ; при , розв’язком буде відрізок , де  - більший з коренів та .

15. Розв’язати нерівність

Розв’язок. Задана нерівність рівносильна сукупності двох систем:

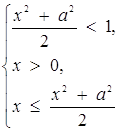 або  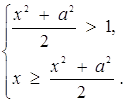Звідси

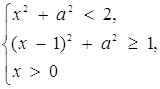 або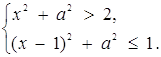

На координатній площині  перша система задає множину точок першого та четвертого координатних кутів, які одночасно лежать всередині кола з центром (0; 0) і радіуса  та поза колом з центром (1; 0) і радіуса 1. Друга система - множина точок, які одночасно лежать поза першим колом, але знаходяться в другому колі. Тоді всі розв’язки початкової нерівності наведено на рис.2.21.

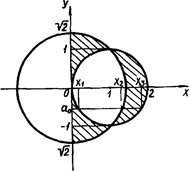
Рис.2.21

Зазначимо, що, наприклад, пряма  (см. рисунок) перетинає кола в точках з абсцисами    Тепер нескладно "прочитати" з рисунка відповідь.

Відповідь: Якщо  то  якщо  то  або  якщо  то немає розв’язків.

Наприкінці, розглянемо технологію складання задач. Розглянемо задачу.

Навести на координатній площині  розв’язок системи нерівностей

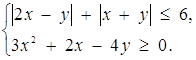
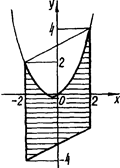
Рис.2.22

На рис.2.22 наведено цей розв’язок (область зі штриховою лінією).

Тепер, замінивши у на а, за допомогою графічного образу легко скласти наступні задачі.

При яких значеннях параметра а система нерівностей

1) має розв’язок? 2) має єдиний розв’язок? 3) має тільки від’ємні розв’язки? 4) має тільки додатні розв’язки? 5) має тільки розв’язки, які задовольняють умові ;

6) має хоча б один розв’язок, якій задовольняє умові ? 7) має розв’язок, який містить відрізок 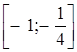? 8) має розв’язки, які містять не більше трьох цілих чисел?

Розділ 3. Застосування похідної

В цьому параграфі наведені задачі, для розв’язання яких використовуються наглядно-графічні міркування, причому при побудові необхідного графічного образу використовується апарат похідної.

1. Скільки розв’язків в залежності від параметра  має рівняння ?

Розв’язання. Перепишемо рівняння у вигляді: . Маємо

, , , , звідки . Отже,

x	(-¥, - 1)	-1	(-1; - 1/Ö5)	-1/Ö5	(-1/Ö5; 1/Ö5)	1/Ö5	(1/Ö5; 1)	1	(1; +¥)
a/ (x)	+	0	-	0	+	0	-	0	+
a (x)	­	0	¯	-16Ö5/125	­	-16Ö5/125	¯	0	­

Побудуємо графік функції .

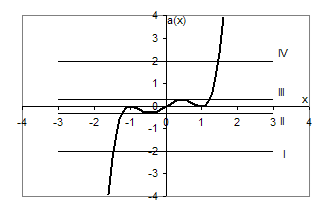
Рис.3.1

Якщ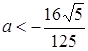о  або 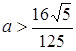, то рівняння має 1 розв’язок (положення І та ІV); якщо  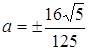(положення ІІ та ІІІ), то рівняння має 2 розв’язки; якщо 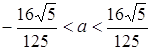, то рівняння має 3 розв’язки (між положеннями ІІ та ІІІ). Відповідь: якщ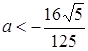о  або 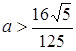, то 1 розв’язок; якщо 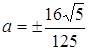, то 2 розв’язки; якщо 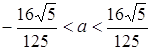, то 3 розв’язки.

2. При яких  рівняння  має три розв’язки? Розв’язання. Перепишемо рівняння у вигляді: , . Знаходимо похідну: , звідки . Отже,

x	(-¥, 0)	(0;1)	1	(1; +¥)
a/ (x)	+	+	0	-
a (x)	­	­	-3	¯

Побудуємо графік функції .

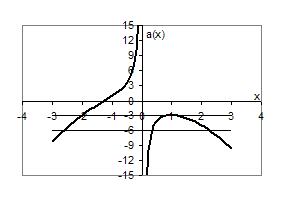
Рис.3.2

Ті значення , для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. Отже, .

Відповідь: .

3. При яких  рівняння  має три розв’язки?

Розв’язання. Перепишемо рівняння у вигляді: . Знаходимо похідну:

, звідки , . Отже,

x	(-¥, - 2)	-2	(-2; 0)	0	(0; +¥)
a/ (x)	+	0	-	0	+
a (x)	­	4/e2	¯	0	­

Побудуємо графік функції .

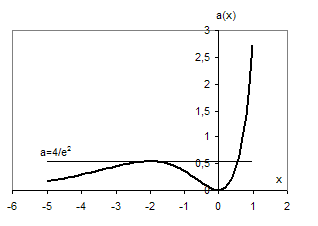
Рис.3.3

Ті значення , для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. Отже, .

Відповідь: .

4. Скільки розв’язків має рівняння  на проміжку ?

Розв’язання. Перепишемо рівняння у вигляді: 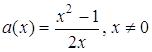. Знаходимо похідну: 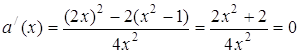. Побудуємо графік функції .

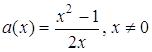Знайдемо значення функції в граничних точках проміжку :

, .

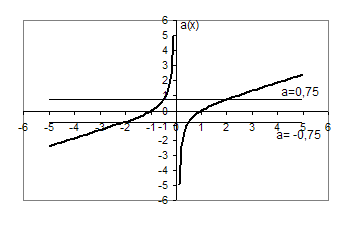
Рис.3.4

З рис.3.4 випливає, що при  або  рівняння має 1 розв’язок; при  рівняння має 2 розв’язки.

Відповідь: якщо  або , то 1 розв’язок; якщо , то 2 розв’язки.

5. При яких значеннях  всі три корені рівняння  дійсні?

Розв’язання. Точка  не є коренем рівняння при ні яких значеннях . Тому запишемо , .

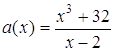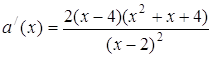Функція  спадає на кожному з проміжків  та (, а зростає на , причому  - точка мінімуму, .

x	(-¥, 2)	(2; 4)	4	(4; +¥)
a/ (x)	-	-	0	+
a (x)	¯	¯	48	­

Побудуємо графік функції .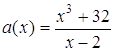

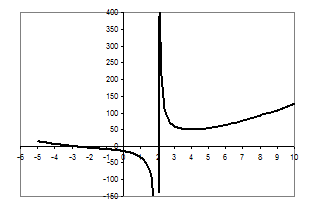
Рис.3.5

Ті значення , для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. З рисунка видно, що .

Відповідь: .

6. Розв’язати рівняння . При яких значеннях параметра  добуток коренів менше найменшого кореня цього рівняння?

Розв’язання. Із заданого рівняння одразу знаходимо , , . Розглянемо функції , , , . Побудуємо графіки цих функцій.

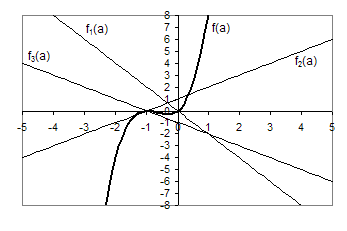
Рис.3.6

Необхідно знайти такі значення параметра, при яких графік  лежить нижче

. Шукані значення - це всі значення, менше , де найменший корінь рівняння . Звідси знаходимо, що . Відповідь: .

7. Визначити як розташовані корені рівняння  відносно відрізка .

Розв’язання. Запишемо . Точки  та  не є коренями заданого рівняння ні при яких . Тоді .

Знайдемо похідну

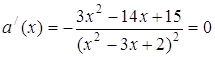
   або .

Точка  - точка мінімуму,  - точка максимуму, , .

Функція  спадає на кожному з проміжків  та зростає на . Графік функції  наведено на рис.3.7.

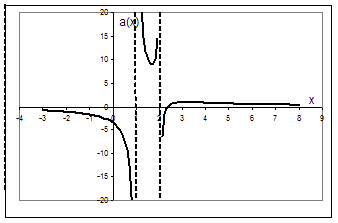
Рис.3.7

Розташування коренів рівняння відносно проміжку  можна визначити, перетинаючи побудований графік горизонтальними прямими. Далі через  позначимо менший корінь, а через  - більший.

Якщо , то ; якщо , то ;

якщо , то ; якщо , то ;

якщо , то ; якщо , то ;

якщо , то ; якщо , то ;

якщо , то рівняння коренів немає; якщо , то ;

якщо , то .

8. При яких значеннях параметра  рівняння  має рівно два корені на відрізку ?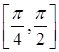

Розв’язання. Запишемо задане рівняння в такому вигляді:

Нехай . Оскільки за умовою , то . Далі, знаходимо

, .

Побудуємо графік функції  для . З

находимо похідну , , .

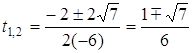x	(-1, )		(; 0)
f/ (x)	-	0	+
f (x)	¯		­

Побудуємо графік функції  для .

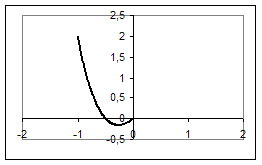
Рис.3.8

Рівняння  має рівно два корені, якщо 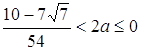. Функція  монотонна на 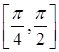, а значить на цьому відрізку кожне своє значення приймає тільки один раз. Відповідь: .

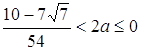9. При яких дійсних  рівняння  має більше одного кореня на відрізку ?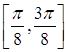

Розв’язання.

Перепишемо рівняння у вигляді

Нехай , оскільки за умовою , то .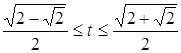

Далі знаходимо, .

Похідна дорівнює

,

, ,

,

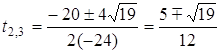
Побудуємо графік функції  (рис.3.9).

Знайдемо 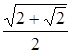a

() =, a () =.

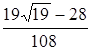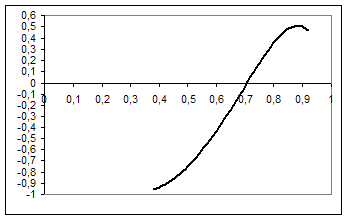
Рис.3.9

Рівняння  має більше одного кореня, якщо .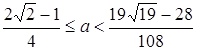

Приблизно це .

Відповідь: .

10. При яких  рівняння 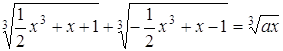 має рівно чотири корені?

Розв’язання. Побудуємо графіки функцій

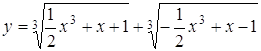 та

.

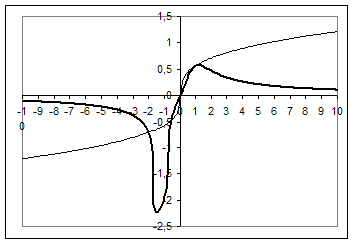
Рис.3.10

Рівняння має чотири розв’язки, коли графік  перетинає 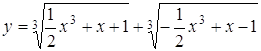 в чотирьох точках (див. рис.3.10)

Відповідь: .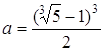

Задачі для самостійної роботи

1. Знайти всі значення , при яких рівняння  має єдиний розв’язок.

Відповідь:  або .

2. Знайти всі значення , при яких для всіх  за модулем не перевищуючих 1, виконується нерівність:

Відповідь:  або .

3. Знайти всі , при кожному з яких область визначення функції  не перетинається з множиною .

Відповідь: .

4. При яких  знайдеться  з інтервала (0,1) таке, що рівняння  має хоча б два розв’язки на інтервалі ?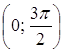

Відповідь: .

5. При - більший з коренів рівняння . Знайти найбільше значення  при , .

Відповідь: .

Список використаної літератури

1.     Вишенський В.О., Перестюк М.О., Самойленко А.М. Задачі з математики. - К.: Вища школа, 1985. - 264 с.

2.     Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. - К.: Євро індекс Лтд, 1995. - 336 с.

3.     Горделадзе Ш.Х., Кухарчук М.М., Яремчук Ф.П. Збірник конкурсних задач з математики: Навч. Посібник. - 3-є вид., - К.: Вища школа, 1988. - 328 с.

4.     Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих в вузы. - М.: Наука, 1976. - 638 с.

5.     Дорофеев Г.В., Затакавай В.В. Решение задач, содержащих параметры. - М.: Перспектива, 1990. - Ч.2. - 38 с.

6.     Цыпкин А.Г., Пинский А.И. Справочник по методам решения задач по математике для средней школы. - 2-е изд. перераб. и доп. - М.: Наука, 1989. - 576 с.

7.     Ястребинецкий Г.А. Задачи с параметрами. - М.: Просвещение, 1986. - 128 с.