Знайти всі значення параметра а, при яких система рівнянь має розв’язки
Знайти всі значення параметра k, при яких система рівнянь має розв’язки
При яких значеннях а система рівнянь не має розв’язків
При яких значеннях параметра а система
Знайти всі значення а, для яких існує пара від’ємних чисел х та у, які задовольняють умові
Знайти всі а, при яких системи рівносильні
Покажіть, що система рівнянь
Визначити число розв’язків системи в залежності від значень параметра а
Знайти всі значення а, при кожному з яких для будь-якого значення b система
Знайти всі значення а, при яких система має єдиний розв’язок
При яких значеннях параметра а система
Навигация
Знайти всі значення параметра k, при яких система рівнянь має розв’язки
Графічні методи розв’язування задач із параметрами
68357
знаков
5
таблиц
91
изображение
1. Знайти всі значення параметра k, при яких система рівнянь має розв’язки
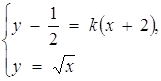
Розв’язання. Прямі сім’ї 
переходять друг в друга шляхом перетворення повороту з центром в точці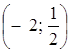 
.
Задана система буде мати Розв’язання, якщо наведені прямі мають з "півпараболою" 
хоча б одну спільну точку.
На рис.1.2.9 відмічені два положення прямої, яким відповідають деякі значення параметра 
и 
.
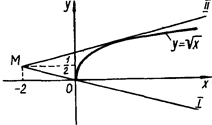
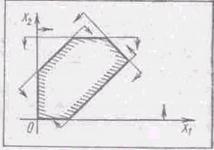
Рис.1.2.9
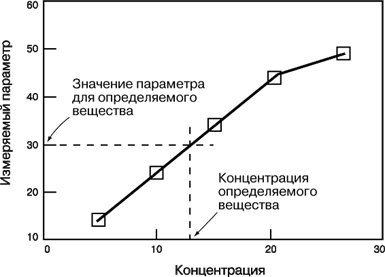
На першій прямій лежить вершина. Друга пряма дотикається "півпараболи". Наглядно очевидно, що якщо прямі сім’ї "заметають" утворений кут (параметр k змінюється від k1 до k2), то система має розв’язки.
Значення k1 знайдемо, підставляючи в перше рівняння системи пару (0; 0). Звідси 
. Значення k2 одержимо, вимагаючи від системи
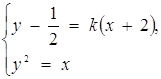
мати єдиний Розв’язання, що рівносильне для рівняння 
при k > 0 мати єдиний корінь. Звідси 
. Відповідь: 
.
Зауваження. В деяких прикладах цього параграфу ми будемо розв’язувати стандартну задачу: для прямої з сім’ї прямих знаходити її кутовий коефіцієнт, який відповідає моменту дотику з кривою. Покажемо, як це робиться в загальному виді за допомогою похідної.
Якщо 
- центр повороту, то координати 
точки дотику з кривою 
можна знайти, розв’язав систему
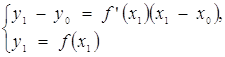
Кутовий коефіцієнт k дорівнює 
.
2. Знайти все значення параметра k, при яких система рівнянь
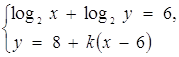
має два різних розв’язки.
Розв’язання. Наступна система рівносильна початковій
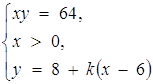
На рис.1.2.10 зображено вітку гіперболи 
при х > 0. Всі прямі, які проходять через точку М (6;
8), складають сім’ю прямих у = 8 + k (x - 6). МА та MB - дотичні до гіперболи.
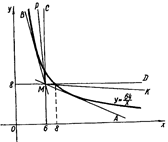
Рис.1.2.10
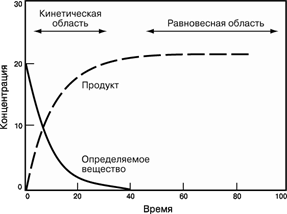
Лише прямі з сім’ї прямих, які проходять між сторонами кутів AMD та ВМС, перетинають гіперболу в двох точках. Можливо здається, що прямі, близькі до вертикального або горизонтального положення, наприклад, МК та МР мають тільки одну спільну точку з гіперболою. Однак це не так: будь-який промінь, який проходить в середині кутів AMD та ВМС і перетинає криву, обов’язково перетне вісь координат, тобто "зіштовхнеться" з гіперболою ще в одній точці.
Кутовий коефіцієнт прямої МА: 
, а прямої MB: 
. Остаточний результат зручно одержати, обертаючи пряму з сім’ї прямих в середині кута AMD проти годинникової стрілки (додатний напрям), а в куті ВМС - за годинниковою стрілкою (від’ємний напрям). Таким чином, 
або 
. Відповідь: або .
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
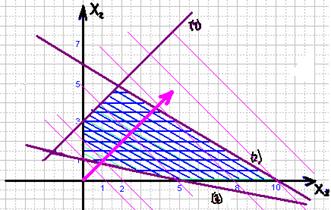
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
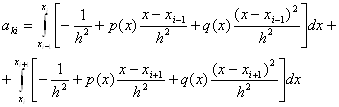
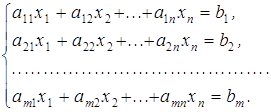
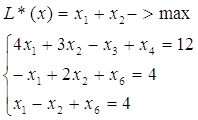
0 комментариев