Навигация
Знайти всі значення а, при кожному з яких для будь-якого значення b система
3. Знайти всі значення а, при кожному з яких для будь-якого значення b система
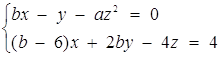
має хоча один розв’язок (х, у, z).
Розв’язання. Маємо систему двох рівнянь с трьома змінними. Однак на цю систему можна дивитися, як на лінійну зі змінними х та у і параметрами а, b, z. Тоді Розв’язання проведемо за схемою, викладеною раніше.
Маємо ![]() - невертикальна пряма. Тоді при
- невертикальна пряма. Тоді при ![]() (друге рівняння системи - вертикальна пряма) система має розв’язок при будь-яких а та z. Якщо
(друге рівняння системи - вертикальна пряма) система має розв’язок при будь-яких а та z. Якщо ![]() , одержимо
, одержимо ![]()
Звідси, якщо ![]() , тобто
, тобто ![]() та
та ![]() , система очевидно має Розв’язання при будь-яких а та z. Однак задача вимагає, щоб b було довільним. Тому необхідно дослідити випадки, коли
, система очевидно має Розв’язання при будь-яких а та z. Однак задача вимагає, щоб b було довільним. Тому необхідно дослідити випадки, коли ![]() та
та ![]() . Для даних значень b рівняння системи задають або паралельні прямі, або співпадаючі. Нас влаштовує, тільки другий випадок. Для цього необхідно вимагати, щоб
. Для даних значень b рівняння системи задають або паралельні прямі, або співпадаючі. Нас влаштовує, тільки другий випадок. Для цього необхідно вимагати, щоб ![]() . При
. При ![]() маємо
маємо ![]() , при
, при ![]() . Залишилося знайти такі а, при яких знайдені рівняння відносно z мають хоча б один Розв’язання, причому одночасно. Оскільки ці рівняння степені не вище другої, то встановлюємо, що
. Залишилося знайти такі а, при яких знайдені рівняння відносно z мають хоча б один Розв’язання, причому одночасно. Оскільки ці рівняння степені не вище другої, то встановлюємо, що ![]() .
.
Відповідь: ![]() .
.
4. Знайти всі а, при яких для будь-якого b існують чотири різні значення с, при яких система 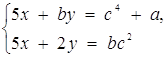 має хоча б один Розв’язання.
має хоча б один Розв’язання.
Розв’язання. При ![]() дана система має єдиний Розв’язання при будь-яких а та с. Оскільки за умовою b - довільне, то розглянемо окремо випадок, коли
дана система має єдиний Розв’язання при будь-яких а та с. Оскільки за умовою b - довільне, то розглянемо окремо випадок, коли ![]() .
.
Знаходимо
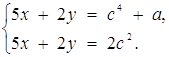
Ця система має Розв’язання, якщо ![]() . Маємо біквадратне рівняння відносно с. Воно має чотири різні розв’язки, якщо відповідне квадратне рівняння має два різних додатних кореня. Для цього достатньо вимагати, щоб а > 0 та D > 0, де
. Маємо біквадратне рівняння відносно с. Воно має чотири різні розв’язки, якщо відповідне квадратне рівняння має два різних додатних кореня. Для цього достатньо вимагати, щоб а > 0 та D > 0, де ![]() . Звідси
. Звідси ![]() .
.
Відповідь: ![]() .
.
5. При яких а та b система 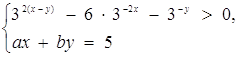 має Розв’язання?
має Розв’язання?
Розв’язання. Перетворимо нерівність системи до вигляду
![]() . Звідси
. Звідси ![]() . Тоді
. Тоді ![]() , тобто
, тобто ![]() . Таким чином, початкова система рівносильна такій:
. Таким чином, початкова система рівносильна такій:
![]()
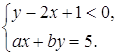
Нерівність системи задає півплощину з межею ![]() (рис.1.4 1).
(рис.1.4 1).
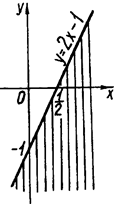
Рис.1.4 1
Система має розв’язок, якщо пряма ![]() перетинає межу півплощини або, будучи паралельна їй, лежить в півплощині
перетинає межу півплощини або, будучи паралельна їй, лежить в півплощині ![]() .
.
Почнемо з випадку b = 0. Тоді рівняння ![]() задає вертикальну пряму, яка перетинає пряму
задає вертикальну пряму, яка перетинає пряму ![]() . Однак це твердження справедливе лише при
. Однак це твердження справедливе лише при ![]() . Значить, при b = 0 та
. Значить, при b = 0 та ![]() система має розв’язки. Далі, при
система має розв’язки. Далі, при ![]() маємо
маємо ![]() . В цьому випадку умова перетину прямих досягається при
. В цьому випадку умова перетину прямих досягається при ![]() тобто
тобто ![]() .
. ![]() Якщо
Якщо ![]() , то прямі або співпадають, або паралельні. Додаючи вимогу
, то прямі або співпадають, або паралельні. Додаючи вимогу ![]() (пряма
(пряма ![]() перетинає вісь ординат нижче точки (0; - 1)), одержимо ще одне взаємне розташування прямих.
перетинає вісь ординат нижче точки (0; - 1)), одержимо ще одне взаємне розташування прямих.
Відповідь: ![]() та
та ![]() , або
, або ![]() та
та ![]() , або
, або ![]() та
та ![]() .
.
6. При яких значеннях параметра а система нерівностей має Розв’язання?
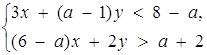
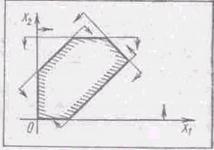
Розв’язання. Якщо межі півплощин, які задають нерівності системи, перетинаються, то дана система має розв’язки.
Очевидно а = 1 підходе. Якщо ![]() , то рівняння меж півплощин перепишемо в такому виді:
, то рівняння меж півплощин перепишемо в такому виді: ![]() та
та ![]() . Ці прямі перетинаються, якщо
. Ці прямі перетинаються, якщо ![]() , тобто
, тобто ![]() та
та ![]() .
.
Розглянемо випадки а = 3 та а = 4. При а = 3 межі співпадають, і очевидно система розв’язків не має (нерівності системи задають різні півплощини). При ![]() маємо
маємо
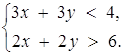
Ця система також розв’язків не має (рис.1.4 2).
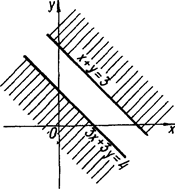
Рис.1.4 2
Таким чином, а = 4 не підходе.
Відповідь: ![]() та
та ![]() .
. ![]()
Розділ 2. Координатна площина (x; a)
Погляд на параметр як на рівноправну змінну знаходить своє відображення в графічних методах. Оскільки параметр "рівний в правах" зі змінною, то йому, природно, можна "виділити" і свою координатну вісь. Таким чином виникає координатна площина ![]() .
.
Відмова від традиційного вибору букв х та у для позначення осей, визначає один з ефективніших методів розв’язку задач з параметрами.
Для того, щоб найбільш повно розкрити можливості цього метода, покажемо його застосування для розв’язування основних типів задач з параметрами.
Дамо самі загальні признаки, які, можливо, допоможуть впізнавати задачі, які підходять під цей метод: в задачі фігурують лише один параметр а та одна змінна х, вони конструюють деякі аналітичні вирази F![]() , G
, G![]() і т.д.; графіки рівнянь F
і т.д.; графіки рівнянь F ![]() = 0, G
= 0, G ![]() = 0 і т.д. в системі координат
= 0 і т.д. в системі координат ![]() будуються нескладно.
будуються нескладно.
Сам процес розв’язування схематично виглядає так.
Спочатку будується графічний образ, потім, перетинаючи отриманий графік прямими, перпендикулярними параметричній вісі, "знімаємо" потрібну інформацію.
1. Знайти всі значення параметра ![]() , при яких система нерівностей
, при яких система нерівностей
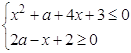
задовольняється лише при одному ![]() .
.
Розв’язання. Перепишемо систему в такому виді:
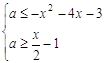
![]()
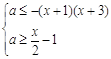
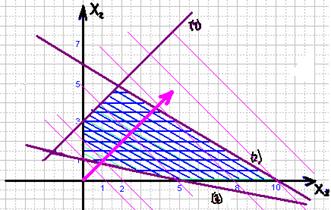
Всі розв’язки цієї системи утворюють область, показану на рисунку штриховою лінією.
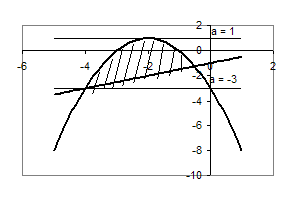
Рис.2.1
Вимога єдності розв’язку даної системи: горизонтальні прямі повинні мати з цією областю тільки одну спільну точку.
Знаходимо точки перетину графіків: ![]() , звідки
, звідки ![]() ,
, ![]() . Тоді
. Тоді ![]() та
та ![]() .
.
Лише прямі ![]() та
та ![]() задовольняють вимозі єдності розв’язку системи.
задовольняють вимозі єдності розв’язку системи.
Відповідь: ![]() та
та ![]() .
.
2. Знайти всі значення параметра ![]() , при яких система нерівностей
, при яких система нерівностей
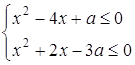
задовольняється лише при одному ![]() .
.
Розв’язання. Перепишемо систему в такому виді:
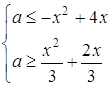 .
.
Всі розв’язки цієї системи утворюють область, показану на рисунку штриховою лінією.
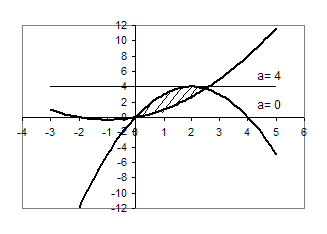
Рис.2.2
Вимога єдності розв’язку даної системи: горизонтальні прямі повинні мати з цією областю тільки одну спільну точку.
Знаходимо точки перетину графіків: 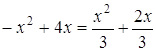 , звідки
, звідки ![]() .
.
З рисунка видно, що лише прямі ![]() та
та ![]() задовольняють вимозі єдності розв’язку системи.
задовольняють вимозі єдності розв’язку системи.
Відповідь: ![]() та
та ![]() .
.
3. При яких значеннях ![]() рівняння
рівняння ![]() має рівно три кореня?
має рівно три кореня?
Розв’язання. Маємо

![]()
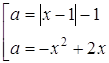
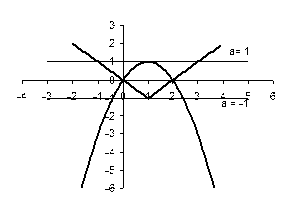
Рис.2.3
Графік цієї сукупності - об’єднання “кута" та параболи.
Лише прямі ![]() та
та ![]() перетинають знайдене об’єднання в трьох точках.
перетинають знайдене об’єднання в трьох точках.
Відповідь: ![]() та
та ![]() .
.
4. При яких значеннях ![]() рівняння
рівняння ![]() має рівно три розв’язки?
має рівно три розв’язки?
Розв’язання. Розв’яжемо задане рівняння як квадратне відносно ![]() :
:
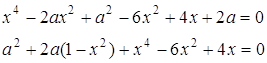
![]()
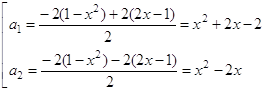
Графік цієї сукупності - об’єднання двох парабол.
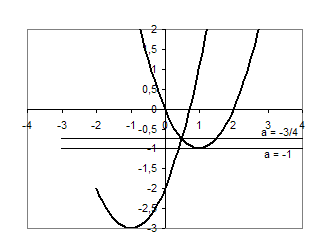
Рис.2.4
Знайдемо точки перетину графіків функцій: ![]() , звідки
, звідки ![]() .
.
![]() та
та ![]() ,
, ![]() .
.
Лише прямі ![]() та
та ![]() перетинають знайдене об’єднання в трьох точках.
перетинають знайдене об’єднання в трьох точках.
Відповідь: ![]() та
та ![]() .
.
5. В залежності від параметра ![]() визначити число коренів рівняння
визначити число коренів рівняння
![]()
Розв’язання. Розв’яжемо задане рівняння як квадратне відносно ![]() :
:
![]()
![]()
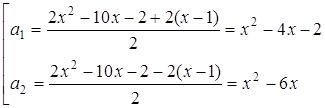
Графік цієї сукупності - об’єднання двох парабол.
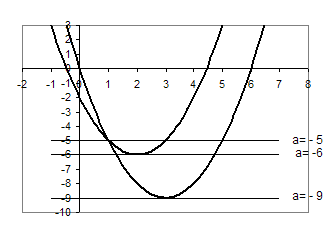
Рис.2.5
Знайдемо координати вершин кожної з парабол:
![]() та
та
![]() .
.
Знайдемо також точки перетину графіків функцій: ![]() , звідки
, звідки ![]() , тоді
, тоді ![]() .
.
Відповідь: якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то 1 розв’язок;
, то 1 розв’язок;
якщо ![]() , то 2 розв’язки; якщо
, то 2 розв’язки; якщо ![]() або
або ![]() , то 3 розв’язки;
, то 3 розв’язки;
якщо ![]() або
або ![]() , то 4 розв’язки.
, то 4 розв’язки.
6. Знайти всі дійсні значення ![]() , для кожного з яких рівняння
, для кожного з яких рівняння
![]()
має тільки два різних коренів. Записати ці корені.
Розв’язання. Перепишемо рівняння у вигляді сукупності:
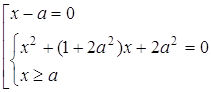
Розв’язками системи є 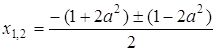 , звідки
, звідки ![]() ,
, ![]() ,
, ![]() .
.
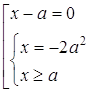 та
та 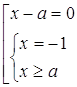
Відповідь: якщо ![]() , то
, то ![]() або
або ![]() ;
;
якщо ![]() , то
, то ![]() або
або ![]() .
.
7. Знайти всі числа ![]() , при яких існує єдине число
, при яких існує єдине число ![]() , яке задовольняє одночасно наступним умовам:
, яке задовольняє одночасно наступним умовам: ![]() та
та ![]() .
.
Розв’язання. Перепишемо систему в вигляді:
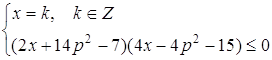
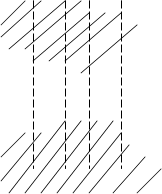
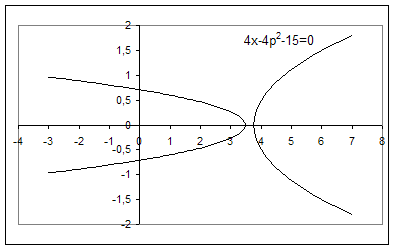
Рис.2.6
На координатній площині ![]() перше рівняння задає сім’ю вертикальних прямих. Параболи
перше рівняння задає сім’ю вертикальних прямих. Параболи ![]() та
та ![]() розбивають площину на 3 частини. Заштрихована область є розв’язком нерівності системи. Це точки, в яких дотичні будуть горизонтальними:
розбивають площину на 3 частини. Заштрихована область є розв’язком нерівності системи. Це точки, в яких дотичні будуть горизонтальними:
![]() або
або ![]() .
.
Відповідь: ![]() або
або ![]() .
.
Задачі для самостійної роботи
1. При яких значеннях а рівняння ![]() має два кореня?
має два кореня?
Розв’язок. Переходимо до рівносильної системи
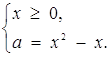
Ця система на координатній площині ![]() задає криву, наведену на рис.2.7 неперервною лінією. Всі точки цієї дуги параболи (і тільки вони) мають координати
задає криву, наведену на рис.2.7 неперервною лінією. Всі точки цієї дуги параболи (і тільки вони) мають координати ![]() , які задовольняють початковому рівнянню. Тому число розв’язків рівняння при кожному фіксованому значенні параметра а дорівнює кількості точок перетину кривої з горизонтальною прямою, яка відповідає цьому значенню параметра. Очевидно при
, які задовольняють початковому рівнянню. Тому число розв’язків рівняння при кожному фіксованому значенні параметра а дорівнює кількості точок перетину кривої з горизонтальною прямою, яка відповідає цьому значенню параметра. Очевидно при ![]() прямі перетинають графік в двох точках, що рівносильне для початкового рівняння мати два кореня.
прямі перетинають графік в двох точках, що рівносильне для початкового рівняння мати два кореня.
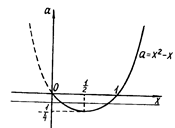
Рис.2.7
Відповідь: ![]()
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
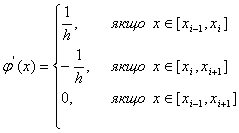
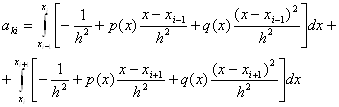
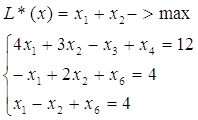
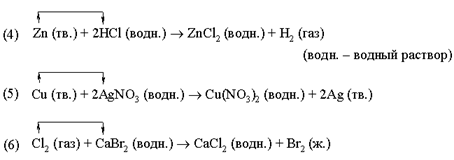

0 комментариев