Знайти всі значення параметра а, при яких система рівнянь має розв’язки
Знайти всі значення параметра k, при яких система рівнянь має розв’язки
При яких значеннях а система рівнянь не має розв’язків
При яких значеннях параметра а система
Знайти всі значення а, для яких існує пара від’ємних чисел х та у, які задовольняють умові
Знайти всі а, при яких системи рівносильні
Покажіть, що система рівнянь
Визначити число розв’язків системи в залежності від значень параметра а
Знайти всі значення а, при кожному з яких для будь-якого значення b система
Знайти всі значення а, при яких система має єдиний розв’язок
При яких значеннях параметра а система
Навигация
При яких значеннях а система рівнянь не має розв’язків
Графічні методи розв’язування задач із параметрами
68357
знаков
5
таблиц
91
изображение
3. При яких значеннях а система рівнянь не має розв’язків
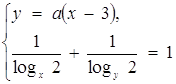
Розв’язання. Система
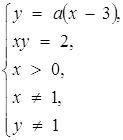
рівносильна початковій.
На рис.1.2.11 точка (3; 0) - центр повороту.
Якщо пряма сім’ї прямих 
обертається в середині кута ОМА, то система не має розв’язків.
Рис.1.2.11
Кутовий коефіцієнт прямої МА дорівнює 
. Тоді при такому повороті параметр а приймає всі значення з проміжку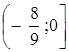 
. (Ми включили 
, оскільки пряма МО не перетинає гіперболу)
Існує ще одна пряма сім’ї прямих, а саме 
, яка проходить через "дірки" в гіперболі. Тому при 
система також не має розв’язків.
Відповідь: або 
.
4. При яких значеннях параметра а рівняння 
має єдиний Розв’язання?
Розв’язання. Розглянемо функції у = ах та 
. Графік другої функції побудуємо, розглянувши рівняння 
при 
. Перетворюючи останнє до виду 
одержимо, що шуканий графік - півколо з центром (4;
1) і радіусом 1.
На рис.1.2.12 це дуга АВ. Всі прямі у = ах, які проходять між променями ОА та 0В перетинають дугу в одній точці. Також одну точку с дугою мають пряма ОВ та дотична ОМ.
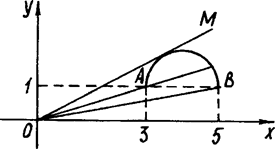
Рис.1.2.12
Кутові коефіцієнти прямих 0В та ОА відповідно дорівнюють 
та 
. Кутовий коефіцієнт дотичної ОМ дорівнює 
. Дійсно, вимагаючи від системи
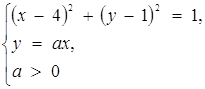
мати єдиний розв’язок, знаходимо 
.
Таким чином, прямі сім’ї у = ах мають з дугою АВ тільки одну спільну точку при 
або 
. Відповідь: або .
5. Визначити, при яких значеннях параметра а мінімум функції 
більше 1.
Розв’язання. Перейдемо до рівносильного формулювання задачі: визначити, при яких значеннях а нерівність 
виконується для всіх х.
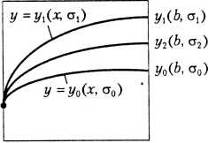
На рис.1.2.13 зображено графік функції 
. Всі прямі сім’ї прямих 
проходять через точку (0;
1) - центр повороту.
Рис.1.2.13
Якщо ці прямі "заповнюють" кут АМВ (МА - дотична), то кожна точка побудованого графіка знаходиться вище відповідних точок прямих. Справедливе й обернене твердження. Знаходячи найбільше значення параметра а, при якому рівняння 
має один Розв’язання, одержимо кутовий коефіцієнт прямої МА. (Менше значення а відповідає моменту дотику прямої з дугою параболи 
) Звідси 
. Для прямої МВ маємо а = 1.
Відповідь: 
.
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
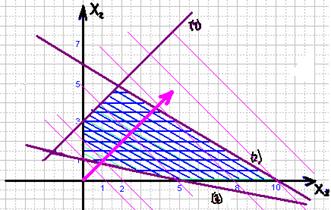
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
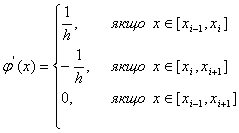
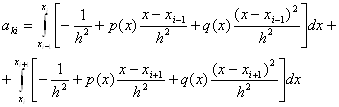
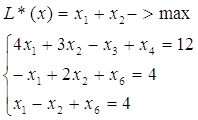
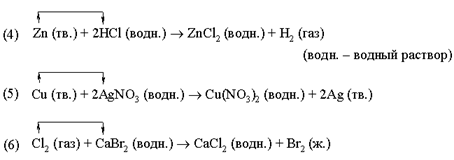
0 комментариев