Навигация
Знайти всі значення а, для яких існує пара від’ємних чисел х та у, які задовольняють умові
8. Знайти всі значення а, для яких існує пара від’ємних чисел х та у, які задовольняють умові
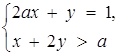
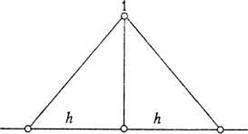
Розв’язання. Нерівність х + 2у > а задає півплощину з "пливучою" межею х + 2у = а. Оскільки очевидно, що а < 0, то система нерівностей ![]()
![]()
![]() задає внутрішню область трикутника ОАВ з координатами вершин О (0; 0), А (0; а), В
задає внутрішню область трикутника ОАВ з координатами вершин О (0; 0), А (0; а), В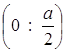 - рис.1.2.16.
- рис.1.2.16.
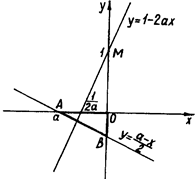
Рис.1.2.16
Все прямі сім’ї прямих ![]() проходять через точку М (0;
проходять через точку М (0;
1). Очевидно початкова система має Розв’язання, якщо прямі сім’ї перетинають вісь абсцис в точках, які лежать між А та О. Для прямої ![]() при фіксованому а абсциса точки перетину с віссю х дорівнює
при фіксованому а абсциса точки перетину с віссю х дорівнює ![]() . Тоді залишилося вимагати, щоб
. Тоді залишилося вимагати, щоб ![]() . Звідси
. Звідси 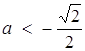 .
.
Відповідь: 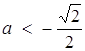 .
.
9. При яких значеннях параметра а рівняння ![]() не має розв’язків?
не має розв’язків?
Розв’язання. Розглянемо функції ![]() та
та ![]() , які задають: сім’ю "кутів" та сім’ю прямих, які проходять через точку
, які задають: сім’ю "кутів" та сім’ю прямих, які проходять через точку 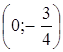 . Оскільки кожен з графіків функцій знаходиться у "русі", то при пошуку їх спільних точок (або умов їх відсутності) виникають ускладнення. Тому спробуємо застосувати такий метод: "зупинимо" один з рухів за допомогою заміни.
. Оскільки кожен з графіків функцій знаходиться у "русі", то при пошуку їх спільних точок (або умов їх відсутності) виникають ускладнення. Тому спробуємо застосувати такий метод: "зупинимо" один з рухів за допомогою заміни.
Нехай ![]() . Тоді
. Тоді ![]() і початкове рівняння приймає вигляд
і початкове рівняння приймає вигляд ![]() . Всі прямі виду
. Всі прямі виду ![]() проходять через точку
проходять через точку 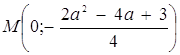 . Оскільки положення точки М не зафіксовано, то поворот не формує сім’ю прямих. Однак сама ідея повороту є результативною.
. Оскільки положення точки М не зафіксовано, то поворот не формує сім’ю прямих. Однак сама ідея повороту є результативною.
Очевидно ордината точки М завжди від’ємна. За допомогою рис.39 легко побачити, що якщо прямі сім’ї прямих проходять між сторонами кута АМВ ![]() , то в цьому і тільки в цьому випадку початкове рівняння має розв’язки.
, то в цьому і тільки в цьому випадку початкове рівняння має розв’язки.
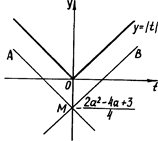
Рис.1.2.17
Таким чином, кутовий коефіцієнт ![]() прямих задовольняє вимозі
прямих задовольняє вимозі ![]() . Звідси
. Звідси ![]()
Відповідь: ![]()
1.3 Гомотетія. Стиск до прямої
1. Знайти число розв’язків системи рівнянь (![]() )
)
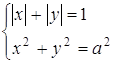
Розв’язання. Побудуємо графіки функцій ![]() (квадрат зі стороною
(квадрат зі стороною ![]() ) та
) та ![]() . Члени сім’ї функцій
. Члени сім’ї функцій ![]() - гомотетичні кола (з центром гомотетії (0,0)).
- гомотетичні кола (з центром гомотетії (0,0)).
Рис.1.3.1
Якщо коло лежить всередині квадрата, то розв’язків немає.
Якщо коло вписане в квадрат, то з’являються розв’язки. В цьому випадку з теореми Піфагора: 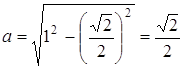 .
.
При 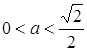 система немає розв’язків, при
система немає розв’язків, при 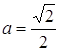 система має 4 розв’язки. Далі зі збільшенням
система має 4 розв’язки. Далі зі збільшенням ![]() (
(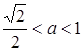 ) кожна сторона квадрата має дві спільні точки перетину з колом (всього 8 розв’язків).
) кожна сторона квадрата має дві спільні точки перетину з колом (всього 8 розв’язків).
При ![]() квадрат вписаний в коло, маємо 4 розв’язки. При
квадрат вписаний в коло, маємо 4 розв’язки. При ![]() розв’язків немає. Відповідь: при
розв’язків немає. Відповідь: при 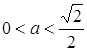 розв’язків немає, при
розв’язків немає, при 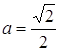 - 4 розв’язки, при
- 4 розв’язки, при 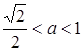 - 8 розв’язків, при
- 8 розв’язків, при ![]() - 4 розв’язки, при
- 4 розв’язки, при ![]() розв’язків немає.
розв’язків немає.
2. При яких дійсних значеннях ![]() система
система
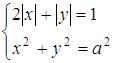
має 8 різних розв’язків?
Розв’язнання. Побудуємо графіки функцій ![]() (ромб зі стороною довжиною
(ромб зі стороною довжиною ![]() ) та
) та ![]() . Члени сім’ї функцій
. Члени сім’ї функцій ![]() - гомотетичні кола (з центром гомотетії (0,0)).
- гомотетичні кола (з центром гомотетії (0,0)).
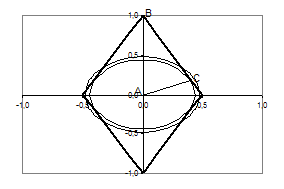
Рис.1.3.2
Знайдемо значення параметра ![]() , при якому коло дотикається до ромба.
, при якому коло дотикається до ромба.
З прямокутного трикутника (зі сторонами ![]() та 1) знайдемо
та 1) знайдемо 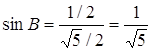 , тоді з трикутника АВС
, тоді з трикутника АВС ![]() , звідки
, звідки 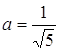 .
.
Зі збільшенням ![]() система буде мати 8 розв’язків (8 точок перетину кола з ромбом). А при
система буде мати 8 розв’язків (8 точок перетину кола з ромбом). А при ![]() система буде мати 4 розв’язки (4 точки перетину з ромбом). Отже,
система буде мати 4 розв’язки (4 точки перетину з ромбом). Отже, 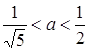 . Відповідь:
. Відповідь: 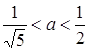
3. Визначити, при яких ![]() система рівнянь
система рівнянь
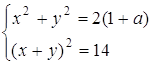
має точно два розв’язки.
Розв’язання. Перепишемо систему рівнянь у вигляді
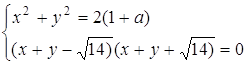
Перше рівняння визначає гомотетичні кола (з центром гомотетії (0,0) та радіусом ![]() ). Друге рівняння - об’єднання двох прямих:
). Друге рівняння - об’єднання двох прямих: ![]() ,
, ![]() . Побудуємо прямі та кола на графіку.
. Побудуємо прямі та кола на графіку.
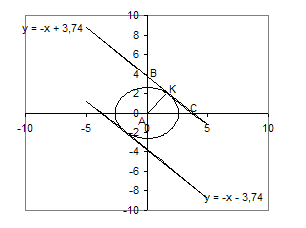
Рис.1.3.3
Система буде мати точно 2 розв’язки, коли коло дотикається двох прямих. Знайдемо параметр ![]() . З
. З ![]() гіпотенуза
гіпотенуза ![]() ,
, 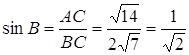 . З
. З ![]()
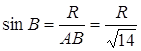 , тоді
, тоді 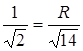 ,
, ![]() . Остаточно знаходимо
. Остаточно знаходимо ![]() . Відповідь:
. Відповідь: ![]() .
.
4. Для кожного від’ємного числа ![]() розв’язати нерівність
розв’язати нерівність ![]() .
.
Розв’язання. Перепишемо нерівність у вигляді ![]() . Побудуємо графіки
. Побудуємо графіки ![]() та
та ![]() . Членами сім’ї функцій
. Членами сім’ї функцій ![]() є гомотетичні півкола (центр гомотетії - точка (0,0)). З нерівності випливає, що півкола повинні лежати вище прямої
є гомотетичні півкола (центр гомотетії - точка (0,0)). З нерівності випливає, що півкола повинні лежати вище прямої ![]() .
.
Кутовий коефіцієнт прямої ![]() дорівнює -2. Тоді
дорівнює -2. Тоді ![]() ,
, ![]() , із
, із ![]() :
: ![]() ,
, ![]() .
.
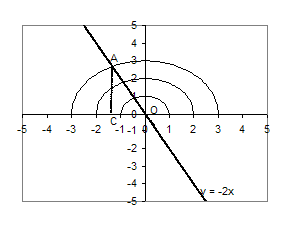
Рис.1.3.4
![]() , звідки
, звідки
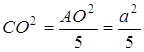 ,
, 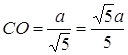 .
.
Розв’язком нерівності для кожного від’ємного числа ![]() буде проміжок
буде проміжок 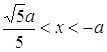 . Відповідь:
. Відповідь: 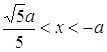 .
.
5. Скільки розв’язків в залежності від ![]() має рівняння
має рівняння ![]() .
.
Розв’язання. Перепишемо рівняння у вигляді ![]() . Побудуємо графіки функцій
. Побудуємо графіки функцій ![]() (гомотетичні кути з вершиною в точці (2,0)) та
(гомотетичні кути з вершиною в точці (2,0)) та ![]() . При
. При ![]() графіки наведені на рисунку 1.3.5
графіки наведені на рисунку 1.3.5
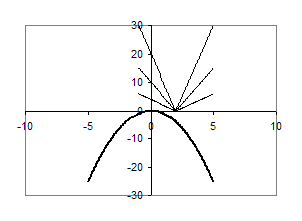
Рис.1.3.5
З рис.1.3.5 видно, що при ![]() спільних точок графіки не мають, рівняння розв’язків немає.
спільних точок графіки не мають, рівняння розв’язків немає.
При ![]() графіки
графіки ![]() та
та ![]() наведені на рисунку 1.3.6.
наведені на рисунку 1.3.6.
З рис.1.3.6 видно, що при ![]()
![]() ,
, ![]() - 1 розв’язок;
- 1 розв’язок;
при ![]() - 2 точки перетину графіків (2 розв’язки);
- 2 точки перетину графіків (2 розв’язки);
при ![]() - 3 точки перетину графіків (3 розв’язки);
- 3 точки перетину графіків (3 розв’язки);
при ![]() - 4 точки перетину графіків (4 розв’язки).
- 4 точки перетину графіків (4 розв’язки).
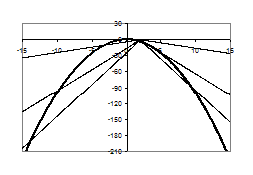
Рис.1.3.6
Відповідь: при ![]()
![]() ,
, ![]() - 1 розв’язок; при
- 1 розв’язок; при ![]() - 2 розв’язки; при
- 2 розв’язки; при ![]() - 3 розв’язки; при
- 3 розв’язки; при ![]() - 4 розв’язки.
- 4 розв’язки.
6. При яких значеннях ![]() криві
криві 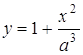 та
та ![]() мають тільки одну спільну точку?
мають тільки одну спільну точку?
Розв’язання. Необхідно розв’язати рівняння 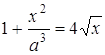 або
або 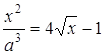 . Побудуємо графіки функцій
. Побудуємо графіки функцій 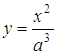 (гомотетичні вітки парабол з центром гомотетії (0,0)) та
(гомотетичні вітки парабол з центром гомотетії (0,0)) та ![]() . ОДЗ рівняння:
. ОДЗ рівняння: ![]() .
.
При ![]() маємо 1 розв’язок.
маємо 1 розв’язок.
Розглянемо випадок дотику двох графіків.
Запишемо рівняння дотичних до кожного з графіків в точці ![]() :
:
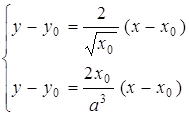 , звідси
, звідси ![]() .
.
Підставляємо ![]() в рівняння
в рівняння 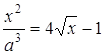 , тоді
, тоді 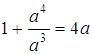 ,
, ![]() .
.
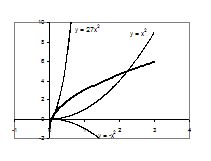
Рис.1.3.7
Відповідь: ![]() або
або ![]() .
.
7. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок, більше одного розв’язку, немає розв’язків?
має єдиний розв’язок, більше одного розв’язку, немає розв’язків?
Розв’язання. Побудуємо графіки функцій ![]() та
та ![]() .
.
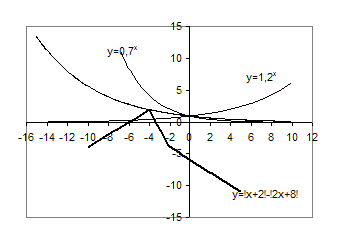
Рис.1.3.8
Розв’яжемо рівняння на проміжку ![]() для того, щоб знайти точку дотику функцій.
для того, щоб знайти точку дотику функцій.
Якщо ![]() , то
, то ![]() ,
, ![]() , при
, при ![]()
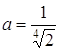 .
.
Таким чином, при 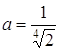 - 1 розв’язок, при
- 1 розв’язок, при 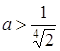 - точки перетину графіків є (більше одного розв’язку), при
- точки перетину графіків є (більше одного розв’язку), при 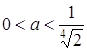 - немає точок перетину графіків (немає розв’язків).
- немає точок перетину графіків (немає розв’язків).
Відповідь: при 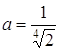 - 1 розв’язок, при
- 1 розв’язок, при 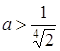 - більше одного розв’язку, при
- більше одного розв’язку, при 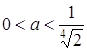 немає розв’язків.
немає розв’язків.
Задачі для самостійної роботи
1. При яких с система має хоча б один розв’язок?
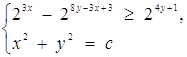
Розв’язання. Спростимо нерівність системи. Маємо ![]() . Нехай
. Нехай ![]() . Тоді
. Тоді ![]() . Звідси з урахуванням того, що
. Звідси з урахуванням того, що ![]() , одержимо
, одержимо ![]() . Запишемо
. Запишемо ![]() , тобто
, тобто ![]() . Таким чином, початкова система рівносильна такій:
. Таким чином, початкова система рівносильна такій:
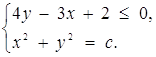
Графіком першої нерівності цієї системи є півплощина з межею ![]() (рис.1.3.9).
(рис.1.3.9).
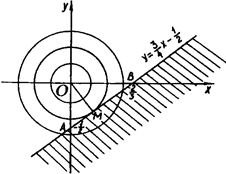
Рис.1.3.9
Очевидно система може мати розв’язки, якщо ![]() . Тоді рівняння
. Тоді рівняння
х 2 + у 2 = с задає сім’ю гомотетичних кіл з центром в точці О (0; 0). Рисунок підказує, що якщо радіус кола не менше довжини відрізка ОМ, тобто відстань від точки О до межі півплощини, то система має розв’язки. Маємо ![]() . З
. З ![]() . Звідси
. Звідси ![]() .
.
Відповідь: ![]() .
.
2. Скільки розв’язків має система в залежності від параметра а?
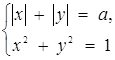
Розв’язання. При ![]() система розв’язків не має. При фіксованому
система розв’язків не має. При фіксованому ![]() графіком першого рівняння є квадрат з вершинами (а; 0), (0; - а), (-а; 0), (0; а). Таким чином, членами сім’ї
графіком першого рівняння є квадрат з вершинами (а; 0), (0; - а), (-а; 0), (0; а). Таким чином, членами сім’ї ![]() є гомотетичні квадрати (центр гомотетії - точка О (0; 0)).
є гомотетичні квадрати (центр гомотетії - точка О (0; 0)).
Якщо квадрат (рис.1.3.10) знаходиться в колі ![]() система розв’язків не має.
система розв’язків не має.
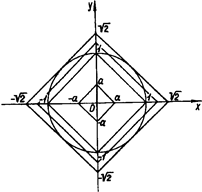
Рис.1.3.10
Зі збільшенням а (квадрат "роздувається") розв’язки з’являються лише в той момент, коли квадрат буде вписаним в коло. В цьому випадку (а = 1) розв’язків буде чотири. Далі, при ![]() кожна сторона квадрата має дві спільні точки з колом, тоді система буде мати вісім розв’язків. При
кожна сторона квадрата має дві спільні точки з колом, тоді система буде мати вісім розв’язків. При ![]() коло буде вписане в квадрат, тобто розв’язків стане знов чотири. Очевидно при
коло буде вписане в квадрат, тобто розв’язків стане знов чотири. Очевидно при ![]() система розв’язків не має.
система розв’язків не має.
Відповідь: якщо ![]() або
або ![]() , то немає розв’язків; якщо
, то немає розв’язків; якщо ![]() або
або ![]() , то розв’язків чотири; якщо
, то розв’язків чотири; якщо ![]() , то розв’язків вісім.
, то розв’язків вісім.
3. Знайти всі значення параметра а, при кожному з яких рівняння ![]() має рівно вісім розв’язків.
має рівно вісім розв’язків.
Розв’язання. Маємо ![]() , де
, де ![]() . Розглянемо функції
. Розглянемо функції ![]() та
та ![]() . Перша з них задає сім’ю гомотетичних півкіл з центром в О (0; 0), друга - сім’ю прямих, паралельних вісі абсцис.
. Перша з них задає сім’ю гомотетичних півкіл з центром в О (0; 0), друга - сім’ю прямих, паралельних вісі абсцис.
З рис.1.3.11 видно, що зі збільшенням радіуса ![]() півкола зростає число коренів початкового рівняння. Їх буде рівно вісім, якщо
півкола зростає число коренів початкового рівняння. Їх буде рівно вісім, якщо ![]() .
.
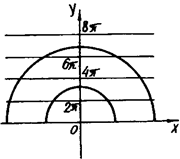
Рис.1.3.11
Зауважимо, що а не є радіусом півкола, т. як ![]() .
.
Відповідь: ![]() або
або ![]() .
.
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
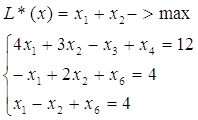

0 комментариев