Навигация
Покажіть, що система рівнянь
2. Покажіть, що система рівнянь

має єдиний розв’язок при всіх значеннях ![]() .
.
Розв’язання. Графіками рівнянь системи є прямі. Перше рівняння при ![]() задає вертикальну пряму
задає вертикальну пряму ![]() , яка перетинає графік другого рівняння, що рівносильне для системи мати єдиний розв’язок. Друге рівняння при
, яка перетинає графік другого рівняння, що рівносильне для системи мати єдиний розв’язок. Друге рівняння при ![]() задає вертикальну пряму
задає вертикальну пряму ![]() , яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
, яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() . Прямі паралельні, якщо
. Прямі паралельні, якщо 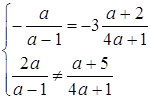 , звідки з першого рівняння
, звідки з першого рівняння ![]() , розв’язків немає. Отже, співпадати прямі також не можуть.
, розв’язків немає. Отже, співпадати прямі також не можуть.
Відповідь: прямі перетинаються при всіх значеннях ![]() .
.
3. Знайти всі значення ![]() , при яких система рівнянь немає розв’язків:
, при яких система рівнянь немає розв’язків:
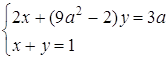
Розв’язання. Графіками рівнянь системи є прямі. Перше рівняння при 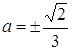 задає вертикальні прямі
задає вертикальні прямі ![]() , які перетинають графік другого рівняння, що рівносильне для системи мати єдиний розв’язок.
, які перетинають графік другого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо 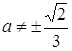 , то
, то ![]() ;
; ![]() .
.
Система немає розв’язків, коли прямі паралельні, тобто
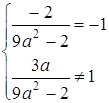
![]()
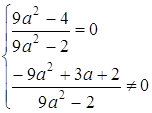
![]()
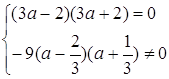
![]()

Відповідь: система немає розв’язків при ![]() .
.
4. При яких значеннях ![]() система рівнянь
система рівнянь
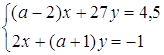
має нескінчену множину розв’язків?
Розв’язання. Графіками рівнянь системи є прямі. Друге рівняння при ![]() задає вертикальну пряму
задає вертикальну пряму ![]() , яка перетинають графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
, яка перетинають графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо ![]() , то
, то ![]() . З першого рівняння маємо
. З першого рівняння маємо ![]() .
.
Система має нескінчену множину розв’язків, коли прямі співпадають, тобто
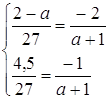
![]()
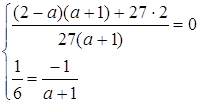
![]()

![]()
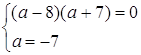
![]()
![]()
Відповідь: система має нескінчену множину розв’язків при ![]() .
.
5. Знайти всі пари значень ![]() , при кожній з яких система рівнянь
, при кожній з яких система рівнянь
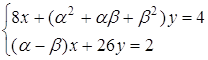
має нескінчену множину розв’язків.
Розв’язання. Перепишемо систему рівнянь у вигляді

Система має нескінчену множину розв’язків, коли прямі співпадають, тобто
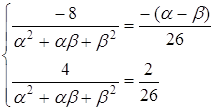
Помножуємо друге рівняння на 2 і додаємо до першого рівняння: ![]() . Виражаємо
. Виражаємо ![]() і підставляємо в друге рівняння:
і підставляємо в друге рівняння:
![]()
![]()
![]() , тоді
, тоді ![]()
Відповідь: ![]() або
або ![]() .
.
6. При яких значеннях ![]() існують розв’язки системи рівнянь
існують розв’язки системи рівнянь
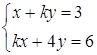 ,
,
які задовольняють одночасно нерівностям ![]() ?
?
Розв’язання. Знаходимо з першого рівняння ![]() і підставляємо в друге рівняння:
і підставляємо в друге рівняння: ![]() , звідки
, звідки ![]() . За умовою задачі
. За умовою задачі![]() , тобто
, тобто ![]() , звідки
, звідки ![]() .
.
Тоді ![]() . За умовою задачі
. За умовою задачі![]() , тобто
, тобто ![]() , звідки
, звідки ![]() ,
, ![]() . Отже,
. Отже, ![]()
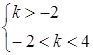
![]()
![]() .
.
Відповідь: ![]() .
.
7. Знайти всі ![]() , при яких рівносильні системи рівнянь
, при яких рівносильні системи рівнянь
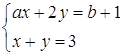 та
та  .
.
Розв’язання. Розглянемо другу систему: 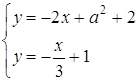 . Ця система має єдиний розв’язок при будь-яких
. Ця система має єдиний розв’язок при будь-яких ![]() (
(![]() ). Для виконання умови рівноправності необхідно, щоб всі чотири прямі, які задаються рівняннями системи, мали спільну точку. Цю точку знайдено, розв’язавши систему
). Для виконання умови рівноправності необхідно, щоб всі чотири прямі, які задаються рівняннями системи, мали спільну точку. Цю точку знайдено, розв’язавши систему

![]()
![]() .
.
Підставимо знайдені значення ![]() в перші рівняння заданих систем:
в перші рівняння заданих систем:

![]()
![]() або
або ![]() .
.
Перша система при ![]() має нескінчено багато розв’язків:
має нескінчено багато розв’язків:
 .
.
Тому системи рівнянь рівносильні при ![]() .
.
Відповідь: ![]() .
.
8. Числа ![]() такі, що система рівнянь
такі, що система рівнянь

має нескінчено багато розв’язків, причому ![]() - один із цих розв’язків. Знайти числа
- один із цих розв’язків. Знайти числа ![]() .
.
Розв’язання. Перепишемо систему у вигляді:
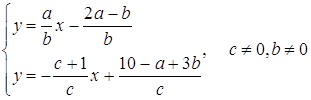 .
.
Система має нескінчену множину розв’язків, коли прямі співпадають, тобто
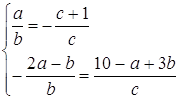
Так як ![]() - один із цих розв’язків системи, то підставимо його в систему:
- один із цих розв’язків системи, то підставимо його в систему:
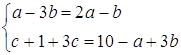
![]()
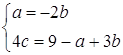
Тоді
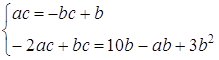
![]()
![]() .
.
З системи трьох рівнянь знаходимо
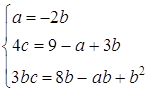
![]()
![]() або
або ![]() .
.
Відповідь: ![]() або
або ![]() .
.
9. Знайти всі значення ![]() , при кожному з яких для будь-якого значення
, при кожному з яких для будь-якого значення ![]() система
система

мала б хоча б один розв’язок ![]()
Розв’язання. Розглянемо задану систему як систему з двома невідомими ![]() та трьома параметрами
та трьома параметрами ![]() Якщо
Якщо ![]() та
та ![]() перепишемо задану систему таким чином:
перепишемо задану систему таким чином:
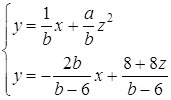
З цієї системи маємо: система має розв’язки, якщо ![]() , тобто
, тобто ![]() та
та ![]() при будь-яких значеннях
при будь-яких значеннях ![]()
При ![]() перше рівняння визначає вертикальну пряму, друге - невертикальну. Таким чином, при
перше рівняння визначає вертикальну пряму, друге - невертикальну. Таким чином, при ![]() система має розв’язок для будь-яких
система має розв’язок для будь-яких ![]() Аналогічно для
Аналогічно для ![]() .
.
Необхідно дослідити систему при ![]() та
та ![]() . При даних значеннях рівняння системи задають або паралельні або співпадаючі прямі. Випадку перетину прямих відповідає рівняння:
. При даних значеннях рівняння системи задають або паралельні або співпадаючі прямі. Випадку перетину прямих відповідає рівняння: 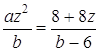
При ![]() маємо
маємо ![]() ,
, ![]() ,
, ![]() ,
, ![]() . При
. При ![]() маємо
маємо 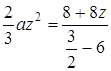 ,
, ![]() ,
, ![]() ,
, ![]() . Таким чином,
. Таким чином, ![]() . Відповідь:
. Відповідь: ![]() .
.
10. Знайти ![]() такі, щоб при будь-яких
такі, щоб при будь-яких ![]() система рівнянь мала б хоча б один розв’язок:
система рівнянь мала б хоча б один розв’язок: 
Розв’язання. Перепишемо систему рівнянь у вигляді: 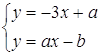 . При
. При![]() задана система має єдиний розв’язок при будь-яких значеннях
задана система має єдиний розв’язок при будь-яких значеннях ![]() . Тому достатньо знайти такі
. Тому достатньо знайти такі ![]() , щоб система мала б розв’язок при
, щоб система мала б розв’язок при ![]() .
.
Маємо ![]() , звідси
, звідси ![]() .
.
Відповідь: ![]()
Задачі для самостійної роботи
Похожие работы
... . Лише за наявності відповідної математичної підготовки слід вимагати від учнів запис та формулювання законв заломлення світла. У новій програмі з фізики для 12 – річної школи багато уваги приділено розв’язуванню фізичних задач. Так, підкреслено , що задачі потрібно ефективно використовувати на всіх етапах засвоєння фізичного знання : для розвитку інтересу, творчіх здібностей і мотивації учнів ...
... іну: , де . Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами: , , . (11.71) Постановка задачі Щоб знайти єдиний розв'язок звичайного диференціального рівняння, необхідно задати деякі допоміжні умови, що використовуються для обчислення інтегрування. Для рі ...
... 20 0 Mf 0 0 0 1 0 0 0 0 Отже, х* = (12, 8, 60), L(x*)max = 20. Задача 3 Для задачі побудувати двоїсту, розв’язати і за розв’язком знайти розв’язок двоїстої: Розв’язання: Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари задач розглянемо на прикладі виробничої задачі. Початкова задача: max z ...
... що знаходяться в стані рівноваги. Для одержання остаточних висновків і підвищення вірогідності застосовуються методи математичного аналізу і математичного моделювання. Розділ ІІ 2.1 Міжпредметні зв’язки при розв’язуванні хімічних задач «Рішення задач – визнаний засіб розвитку мислення, яке легко поєднується з іншими засобами і прийомами навчання» (Цитович І.К.). При вивченні курсу хімії ...
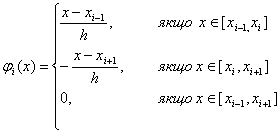
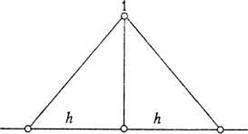
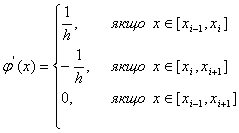
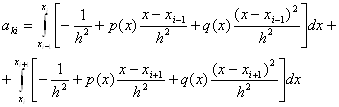
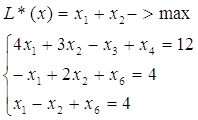

0 комментариев