Первоначальное осмысление статистической закономерности

3.1 Первоначальное осмысление статистической закономерности

Закон больших чисел занимает одно из центральных мест в теории вероятностей. До недавнего времени проблема закона больших чисел не была окончательно решена. Рассмотрим динамику развития этого закона.

Одним из первых к пониманию статистической закономерности и закона больших чисел подошёл Кардано. Относительно своего заключения о 6 возможностях получить одинаковые числа очков на двух костях и 30 возможностях – разные, он пишет: «Целая серия игр (36 бросков) не даёт отклонения, хотя в одной игре это может случиться…, при большом числе игр оказывается, что действительность весьма приближается к этому предположению» [1].

Здесь Кардано утверждает, что при малом количестве наблюдений частота может отклоняться довольно сильно от доли, или, другими словами, – от вероятности; при большом числе испытаний это отклонение будет незначительно.

3.2 Появление теорем Бернулли и Пуассона – простейших форм закона больших чисел

Я. Бернулли писал: «…И что не дано вывести a priori то, по крайней мере, можно получить a posteriori, т.е. из многократного наблюдения результатов…».

Бернулли утверждает, что если в азартных играх всегда можно посчитать число случаев, а сами случаи встречаются одинаково легко, то в других явлениях в природе и обществе ни то ни другое не имеет.

«Всё дело сводится к тому, чтобы для правильного составления предложений о какой-либо вещи были точно исчислены как числа случаев, так и было бы определено насколько одни случаи могут легче встретиться, чем другие…». Но это совершенно невозможно сделать для большинства явлений. Однако Бернулли нашёл выход из сложившейся ситуации. Он утверждает, что при увеличении числа испытаний, частота появления какого-либо события будет мало отличаться от вероятности появления этого события. И чем больше число испытаний, тем меньше это отличие. «Следует заметить, что отношение между числами случаев, которые мы желаем определить опытом, понимается не в смысле точного отношения…, но до известной степени приближённого, т.е. заключённого в двух границах, которые можно взять сколь угодно тесными».

В помощь доказательству своей теоремы Бернулли доказывает ряд лемм [1].

Лемма 1.

Рассматриваются два ряда

0, 1, 2, …, r – 1, r, r + 1, …, r + s;

0, 1, 2, …, nr – n, …, nr, …, nr + n, …, nr + ns

и утверждается, что с увеличением n растёт количество членов между nr и nr + n; nr и nr – n; nr + n и nr + ns; nr и 0. Кроме того, как бы велико ни было n, число членов после nr + n не будет превышать более чем в s – 1 раз число членов, заключённых между nr и nr + n или между nr и nr – n, а также число членов до nr – n не будет превышать более чем в r – 1 раз число членов между теми же числами.

Доказательство.

Найдём количество членов между указанными в лемме членами рассматриваемых рядов. Для этого введём обозначения:

-число членов между nr и nr+n;

-число членов между nr и nr-n;

-число членов между nr+n и nr+ns;

-число членов между nr и 0;

-число членов после nr+n;

-число членов до nr-n.

;

;

;

.

Очевидно, что с увеличением n (т.е. при ) , , ,  будут неограниченно возрастать.

Найдём число членов после nr+n (), очевидно, что ==.

Очевидно, что ==, т.е. число членов после nr+n не превышает более чем в s-1 раз число членов заключённых между nr и nr+n или между nr и nr-n, для любого n.

Найдём число членов до nr-n (), очевидно, что , а значит ==, т.е. число членов до nr-n не превышает более чем в r-1 раз число членов заключённых между nr и nr+n или между nr и nr-n, для любого n.

Что и требовалось доказать.

Лемма 2.

Всякая целая степень какого-либо двучлена r + s выражается числом членов, на единицу большим числа единиц в показателе степени.

Доказательство.

Рассмотрим , где x (x – целое число)

= .

Составим ряд из степеней одночлена s (или r)

0,1,2,…, x-2, x-1, x. Число членов в этом ряду равно x+1.

Т. о. всякая целая степень двучлена r + s выражается числом членов, на единицу большим числа единиц в показателе степени. Что и требовалось доказать.

Лемма 3.

В любой степени двучлена r + s, по крайней мере в t=r+s или nt=nr+ns, некоторый член M будет наибольшим, если числа предшествующих ему и следующих за ним членов находятся в отношении s к r или, что то же, если в этом члене показатели букв r и s находятся в отношении самих количеств r и s; более близкий к нему член с той и другой стороны больше более удалённого с той же стороны; но тот же член M имеет к более близкому меньшее отношение, чем более близкий к более удалённому при равном числе промежуточных членов.

Доказательство.

Отмечается, что коэффициенты членов равноудалённых от концов равны. Число всех членов nt+1=nr+ns+1. Наибольший член будет:

M==.

M можно записать в другом виде, воспользовавшись следующей формулой .

M==.

Ближайший к нему слева член равен ;

справа – .

Следующий слева – ;

справа –  и т.д.

; ;

; , и т.д.

Очевидно, что:

, M-наибольший член.

Что и требовалось доказать.

Лемма 4.

В степени двучлена с показателем nt число n может быть взято столь большим, чтобы отношение наибольшего члена M к двум другим L и , отстоящим от него налево и направо на n членов, превзошло всякое данное отношение.

Доказательство.

M==;

L=;

=.

Для доказательства леммы необходимо установить, что

 и .

===

=.

===

=.

Но эти отношения будут бесконечно большими, когда n полагается бесконечным, ибо тогда исчезают числа 1, 2, 3 и пр. по сравнению с n, и сами числа , ,  и пр. , ,  и пр. будут иметь те же значения, как  и . После этого отбросив эти числа и проведя соответствующие сокращения на n, получим, что

=; =.

Количество сомножителей в числителе и знаменателе равно n. Вследствие чего эти отношения будут бесконечными степенями выражений:  и  и поэтому бесконечно большими.

Таким образом, мы выяснили, что в бесконечно высокой степени двучлена отношение наибольшего члена к другим L и  превосходит всякое заданное отношение.

 и .

Что и требовалось доказать.

Лемма 5.

Отношение суммы всех членов от L до  ко всем остальным с увеличением n может быть сделано больше всякого заданного числа.

Доказательство.

M – наибольший член разложения.

Пусть соседние с ним слева будут F, G, H,…;

пусть соседние с L слева будут P, Q, R,….

На основании леммы 3 имеем:

<;<;<, … или <<<<….

Так как по лемме 4, при n бесконечно большом, отношение  бесконечно, то тем более будут бесконечными отношения , , ,…, и потому отношение  также бесконечно, т.е. сумма членов между наибольшим M и пределом L бесконечно больше суммы такого же числа членов за пределом L и наиболее к нему близких. И так как число всех членов за пределом L превышает, по лемме 1, не более чем в s-1 раз (т.е. конечное число раз) число членов между этим пределом и наибольшим членом M, а сами члены делаются тем меньше, чем дальше они отстоят от предела, по первой части леммы 3, то сумма всех членов между M и L (даже не считая M) будет бесконечно больше сумм всех членов за пределом L. Аналогичное утверждение можно доказать относительно членов между M и . Оба эти утверждения и доказывают лемму.

Что и требовалось доказать.

Главное предложение.

Пусть число благоприятных случаев относится к числу неблагоприятных точно или приближённо, как r к s, или к числу всех случаев, как r к r+s или r к t, это отношение заключается в пределах  и . Требуется доказать, что можно взять столько опытов, чтобы в какое угодно данное число раз (c раз) было вероятнее, что число благоприятных наблюдений попадёт в эти пределы, а не вне их, т.е. отношение числа благоприятных наблюдений к числу всех будет не более чем  и не менее .

Доказательство.

Пусть число необходимых наблюдений будет nt. Вероятность того что все наблюдения будут благоприятны, равна

,

что все кроме одного–

,

кроме двух

 и т.д.

А это есть члены разложения (r+s) в степени nt (делённые на ), которые исследовались в прошлых леммах. Все дальнейшие выводы основываются на доказанных леммах. Число случаев с ns неблагоприятными набдюдениями и nr благоприятными даёт член M. Число случаев, при которых будет nr+n или nr-n благоприятных наблюдений, выражается членами L и , отстоящих на n членов от M. Следовательно, число случаев, для которых благоприятных наблюдений окажется не более nr+n и не менее nr-n, будет выражаться суммой членов, заключённых между L и . Общее же число случаев, для которых благоприятных наблюдений будет или больше nr+n или меньше nr-n, выражается суммой членов, стоящих левее L и правее .

Так как степень двучлена может быть взята столь большая, чтобы сумма членов, заключённых между обоими пределами L и  превосходила более чем в c раз сумму всех остальных из этих пределов выходящих, по леммам 4-й и 5-й, то, следовательно, можно взять столь большое число наблюдений, чтобы число случаев, при которых отношение числа благоприятных наблюдений к числу всех оказывается заключённым в пределы  и  или  и , превышало более чем в c раз число остальных случаев, т.е. сделалось более чем в c раз вероятнее, что отношение числа благоприятных наблюдений к числу всех заключается в пределах  и , а не вне этих пределов.

Что и требовалось доказать.

Для сравнения дадим современную формулировку теоремы Бернулли.

Теорема Бернулли.

Если вероятность наступления события A в последовательности независимых испытаний постоянна и равна p, то, каково бы ни было положительное число , с вероятностью как угодно близкой к единице, можно утверждать, что при достаточно большом числе испытаний n разность  по абсолютной величине окажется меньшей, чем :

,

где –любое малое число.

Эта теорема будет доказана нами позже (после введения неравенства Чебышева).

Всегда может случиться, что, каким бы большим ни было n, в данной серии из n испытаний  окажется больше . Но, согласно теореме Бернулли мы можем утверждать, что если n достаточно велико и если произведено достаточно много серий испытаний по n испытаний в каждой серии, то в подавляющем числе серий неравенство  будет выполнено.

Бернулли считает, что из доказанной теоремы «вытекает то удивительное, по-видимому, следствие, что если бы наблюдения над всеми событиями продолжать всю вечность (причём вероятность, наконец, перешла бы в полную достоверность), то было бы замечено, что всё в мире управляется точными отношениями и постоянным законом изменения, так, что даже в вещах, в высшей степени случайных, мы принуждены были бы признать как бы некоторую необходимость и, скажу я, рок».

А.А. Марков писал, что в этой работе Бернулли «впервые была опубликована и доказана знаменитая …теорема, положившая начало закону больших чисел…». Пуассон (1781–1840 гг.) в своей работе «Исследования о вероятности судебных приговоров по уголовным и гражданским делам» занимался предельными предложениями. В результате он доказал свою знаменитую теорему, которой дал название «закон больших чисел» [1]. Теорема Пуассона формулировалась следующим образом.

Теорема.

Если производится n независимых испытаний, результатами которых является наступление или не наступление события A, причём вероятность наступления события в отдельных испытаниях неодинакова, то с вероятностью, сколь угодно близкой к единице (или, другими словами, – к достоверности), можно утверждать, что частота  наступления события A будет сколь угодно мало отличаться от средней арифметической  вероятностей наступления события в отдельных испытаниях.

Теперь эту теорему записывают так: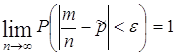

Если же вероятность наступления события не будет изменяться от испытания к испытанию, то =p, и теорема Пуассона в этом случае переходит в теорему Я. Бернулли, которая, таким образом, является частным случаем теоремы Пуассона.

Похожие работы

Динамика развития внутреннего "Я" личности

Скачать

66904

2

0

... о самом себе, как правило, кажутся ему убедительными независимо от того, основываются ли они на объективном знании или субъективном мнении, являются ли они истинными или ложными. 5. Динамика развития внутреннего «Я» индивида Самосознание в первые два года жизни На первых порах младенцы не могут провести грань между собой и окружающим их миром. Однако постепенно они начинают понимать, что ...

Основы экономической теории. Теория Джона М. Кейнса

Скачать

135132

2

0

... регулирования природопользователя, но продолжает уничтожать колоссальные дары природы. Нет сомнения, что изобретательный человеческий ум в конце, концов все же найдет им замену. Теория Джона Мейнарда Кейнса Дж. М. Кейнс – своего рода революционер экономической науки нашего века. Английский экономист, влияние которого на экономическую мысль в XX века сравнимо с воздействием Адама Смита и Давида ...

Динамика развития смысловой стороны речи у младших школьников

Скачать

15958

0

0

... грамматических конструкций ограничено. Дети из группы с относительной слабостью третьего блока мозга обнаружили промежуточные результаты по лексико-синтаксическим показателям. Качественный анализ смыслового уровня речи обнаружил принципиально разные трудности детей трех групп: Для детей с относительной слабостью третьего блока мозга характерно большое количество пропусков смысловых звеньев, ...

Экономическая теория

Скачать

826315

4

1

... равенства и неравенства. При полном равенстве в распределении доходов "кривая Лоренца" представляла бы собой прямую и, наоборот, кривизна усиливается по мере роста неравенства. В соответствии с современной экономической теорией нежелательно как абсолютное равенство в распределении доходов, так и резкий разрыв в уровне жизни различных групп населения. Абсолютное равенство в доходах не стимулирует ...