Неравенство Чебышева. Закон больших чисел в форме Чебышева

3.3 Неравенство Чебышева. Закон больших чисел в форме Чебышева

17.12.1866 г. Чебышев доложил Академии наук свою работу «О средних величинах», которая была опубликована в 1867 г. В «Математическом сборнике». В этой работе Чебышев доказал одно важное неравенство, которое теперь называется неравенством Чебышева. При помощи этого неравенства Чебышев получил теорему, из которой как следствия получаются теоремы Бернулли и Пуассона. В начале работы «О средних величинах» Чебышев доказывает теорему [1,6].

Теорема.

Если математическое ожидание величин x, y, z,… суть a, b, c,…,

а математическое ожидание квадратов , , ,… суть , , ,…, то вероятность, что сумма x+y+z+… заключается в пределах

,

,

при всяком значении  остаётся больше .

Далее Чебышев переходит к следующей теореме.

Если мы изобразим через N число величин x, y, z,…, u, полагая в доказанной сейчас теореме 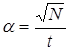, разделим на N как сумму x+y+z+…, так и пределы её

,

,

то из этой теоремы получим следующую относительно средних величин.

Теорема.

Если математическое ожидание величин

x, y, z,…,, , ,… суть a, b, c,…,, , ,…, то вероятность, что среднее арифметическое N величин x, y, z,…, от среднего арифметического математических ожиданий этих величин разнится не более как на 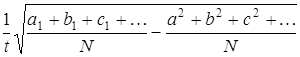 при всяком значении, будет превосходить .

Это и есть знаменитое неравенство Чебышева, которое в современной форме записывается следующим образом:

,

где случайная величина x имеет конечную дисперсию , а –любая отличная от нуля положительная величина.

Действительно, первую теорему Чебышева можно записать так:

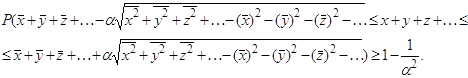
Применим эту теорему к случайной величине x:

.

Но ,

,

,

.

Пусть , тогда 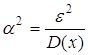 и получаем привычную формулу для неравенства Чебышева .

Сформулируем соответствующую теорему и докажем в ней это неравенство.

Теорема.

Пусть имеется случайная величина  с математическим ожиданием  и дисперсией . Неравенство Чебышева утверждает, что, каково бы ни было положительное число , вероятность того, что величина  отклонится от своего математического ожидания не меньше чем на , ограничена сверху величиной :

.

Доказательство.

1. Пусть величина  дискретная, с рядом распределения

Изобразим возможные значения величины  и её математическое ожидание  в виде точек на числовой оси Ox.

Зададимся некоторым значением  и вычислим вероятность того, что величина  отклонится от своего математического ожидания не меньше чем на : .

Для этого отложим от точки  вправо и влево по отрезку длиной ; получим отрезок . Вероятность  есть не что иное, как вероятность того, что случайная точка  попадёт не внутрь отрезка , а вовне его (концы отрезка мы в него не включаем): .

Для того чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений , которые лежат вне отрезка . Это мы запишем следующим образом:

, где запись  под знаком суммы означает, что суммирование распространяется на все те значения , для которых точки  лежат вне отрезка .

С другой стороны, напишем выражение дисперсии величины  по определению:

.

Так как все члены суммы  неотрицательны, она может только уменьшиться, если мы распространим её не на все значения , а только на некоторые, в частности на те, которые лежат вне отрезка :

.

Заменим под знаком суммы выражение  через . Так как для всех членов суммы , то от такой замены сумма тоже может только уменьшиться, значит:

.

Но согласно формуле  сумма, стоящая в правой части этого неравенства есть не что иное, как вероятность попадания случайной точки вовне отрезка , следовательно , откуда непосредственно вытекает доказываемое неравенство.

2. В случае когда величина  непрерывна, доказательство проводится аналогичным образом с заменой вероятностей  элементом вероятности, а конечных сумм – интегралами. Действительно,

,

где – плотность распределения величины . Далее, имеем:

,

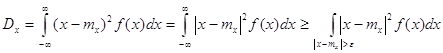откуда и вытекает неравенство Чебышева для непрерывных величин.

Что и требовалось доказать.

Как следствие из своего неравенства Чебышев получает следующую теорему.

Теорема.

Если математические ожидания величин  не превосходят какого-либо конечного предела, то вероятность, что среднее арифметическое N таких величин от среднего арифметического их математических ожиданий разнится менее чем на какую-нибудь данную величину, с возрастанием числа N до, приводится к единице.

Доказательство.

Действительно, рассмотрим случайную величину , представляющую собой среднюю арифметическую из данных случайных величин.

;

;

.

Если ограничены математические ожидания случайных величин и их квадратов, то ограничены также и дисперсии, т.е. Все , где c-некоторое число. Тогда .

Применим теперь неравенство Чебышева к :

, или

.

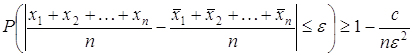Переходя к пределу, получаем:

.

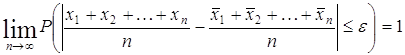Что и требовалось доказать.

Это и есть теорема Чебышева – закон больших чисел Чебышева. Эта теорема устанавливает, что при достаточно больших n с вероятностью, близкой к единице, можно полагать, что среднее арифметическое случайных величин как угодно мало колеблется около некоторого постоянного числа–среднего их математических ожиданий.

Теоремы Пуассона и Бернулли являются частными случаями закона больших чисел Чебышева.

Действительно, пусть в n испытаниях, событие A наступает с вероятностями  и не наступает с вероятностями . Рассмотрим случайную величину – число наступлений события A в i-ом испытании. Тогда

; ; ,

 удовлетворяет условиям теоремы Чебышева, т.е.

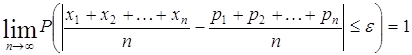, или

,

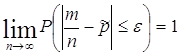где –среднее арифметическое из вероятностей наступлений событий в отдельных испытаниях. А это и есть теорема Пуассона.

Если все , то и , и мы получим теорему Бернулли:

.

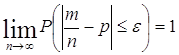Любопытно, что Чебышев не называл доказанную теорему «законом больших чисел», хотя теорема Пуассона получается из неё как частный случай.

Зная, что теорема Бернулли является частным случаем теоремы Чебышева попробуем доказать её как прямое следствие закона больших чисел Чебышева (т.е. приведём современное доказательство теоремы Бернулли [3]). Повторим современную формулировку теоремы Бернулли.

Теорема.

Пусть производится n независимых опытов. Если вероятность наступления события A в последовательности независимых испытаний постоянна и равна p, то, каково бы ни было положительное число , с вероятностью как угодно близкой к единице, можно утверждать, что при достаточно большом числе испытаний n разность  по абсолютной величине окажется меньшей, чем :

,

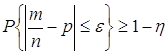где –любое малое число.

Доказательство.

Рассмотрим независимые случайные величины:

–число появлений события A в первом опыте;

–число появлений события A во втором опыте, и т.д.

Все эти величины прерывны и имеют один и тот же закон распределения, выражаемый рядом вида:

т.к. событие A наступает с вероятностью p и не наступает с вероятностью q .

Вычислим математическое ожидание каждой из величин :

, дисперсию:

.

 удовлетворяют условиям теоремы Чебышева, т.е. можем применить неравенство Чебышева:

.

Т.к. , , 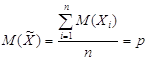а , то получаем выражение:

.

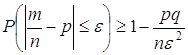Отсюда и следует справедливость доказываемого неравенства:

,

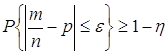где –малое число при .

Что и требовалось доказать.

Похожие работы

Динамика развития внутреннего "Я" личности

Скачать

66904

2

0

... о самом себе, как правило, кажутся ему убедительными независимо от того, основываются ли они на объективном знании или субъективном мнении, являются ли они истинными или ложными. 5. Динамика развития внутреннего «Я» индивида Самосознание в первые два года жизни На первых порах младенцы не могут провести грань между собой и окружающим их миром. Однако постепенно они начинают понимать, что ...

Основы экономической теории. Теория Джона М. Кейнса

Скачать

135132

2

0

... регулирования природопользователя, но продолжает уничтожать колоссальные дары природы. Нет сомнения, что изобретательный человеческий ум в конце, концов все же найдет им замену. Теория Джона Мейнарда Кейнса Дж. М. Кейнс – своего рода революционер экономической науки нашего века. Английский экономист, влияние которого на экономическую мысль в XX века сравнимо с воздействием Адама Смита и Давида ...

Динамика развития смысловой стороны речи у младших школьников

Скачать

15958

0

0

... грамматических конструкций ограничено. Дети из группы с относительной слабостью третьего блока мозга обнаружили промежуточные результаты по лексико-синтаксическим показателям. Качественный анализ смыслового уровня речи обнаружил принципиально разные трудности детей трех групп: Для детей с относительной слабостью третьего блока мозга характерно большое количество пропусков смысловых звеньев, ...

Экономическая теория

Скачать

826315

4

1

... равенства и неравенства. При полном равенстве в распределении доходов "кривая Лоренца" представляла бы собой прямую и, наоборот, кривизна усиливается по мере роста неравенства. В соответствии с современной экономической теорией нежелательно как абсолютное равенство в распределении доходов, так и резкий разрыв в уровне жизни различных групп населения. Абсолютное равенство в доходах не стимулирует ...