Усиление закона больших чисел. Появление необходимого и достаточного условий применимости закона больших чисел

3.5 Усиление закона больших чисел. Появление необходимого и достаточного условий применимости закона больших чисел

В 1923 г. А.Я. Хинчин установил закон повторного логарифма, который является своеобразным обобщением и усилением закона больших чисел[1]. Рассмотрим полученные им результаты.

Согласно теореме Бернулли, при  для любого

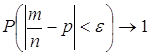
В 1909 г. Борель для  доказал, что 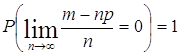, т.е. что для больших  с подавляющей вероятностью должна быть мала в сравнении с , .

В 1917 г. Кантелли распространил результат Бореля на любое .

В 1913 г. Хаусдорф для случая Бернулли нашёл следующую оценку: с вероятностью единица , где  произвольно.

В 1914 г. Харди и Литтльвуд показали, что с вероятностью единица .

А в 1923 г. Хинчин доказал следующую теорему.

Теорема.

Если вероятность появления события A в каждом из  независимых испытаний равна , то число  появлений события A в  испытаниях при  удовлетворяет соотношению:

.

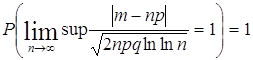Функция  в этом смысле является точной верхней границей случайной величины .

Представим этот результат геометрически. Будем по оси абсцисс откладывать , а по оси ординат – . Проведём в этой системе прямые:  и . Теорема Бореля-Кантелли утверждает, что при достаточно больших  почти достоверно, что  будет заключаться между прямыми  и . Но эти границы оказались очень широки и Хинчин указал более строгие границы изменения . Если мы проведём кривые

 и (3.5.1)

, (3.5.1')

то по теореме Хинчина, каково бы ни было , для достаточно больших  разность  почти достоверно заключена между этими кривыми. Если же взять кривые

 и (3.5.2)

, (3.5.2')

то  почти достоверно бесконечно много раз выйдет за пределы этих кривых. Изобразим схематически эту ситуацию.

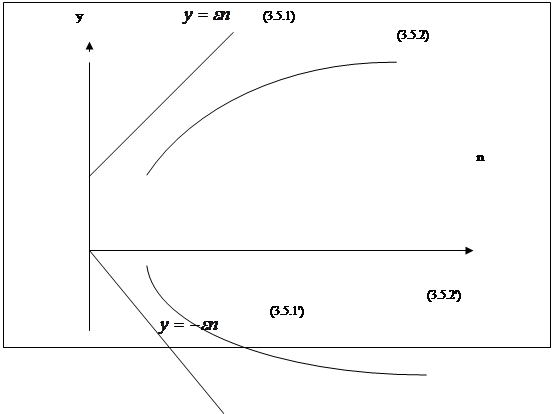
Хотя Марков и расширил границы применимости закона больших чисел, однако, окончательно этот вопрос ещё не был решён. Установить необходимые и достаточные условия применимости закона больших чисел удалось только благодаря применению методов и понятий теории функций.

В 1926 г. А.Н. Колмогоров установил эти условия в своей работе [5].

Определение.

Случайные величины  последовательности  называются устойчивыми, если существует такая числовая последовательность , что для любого положительного  , .

Если существуют все  и если можно положить , то говорят, что устойчивость нормальная.

Если все  равномерно ограничены, то из , , следует соотношение , , и, следовательно, , .

Таким образом, устойчивость ограниченной последовательности необходимо нормальна. Пусть .

По неравенству Чебышева .

Следовательно, условие Маркова: , , достаточно для нормальной устойчивости.

Если  равномерно ограничены, , то по неравенству ,

.

Следовательно, в этом случае условие Маркова является также и необходимым для нормальной устойчивости .

Если  и величины  попарно некоррелированы, то .

Следовательно, в этом случае для нормальной устойчивости средних арифметических , т.е. для того, чтобы для всякого

,

Достаточно выполнения следующего условия:  (теорема Чебышева). В частности, это условие выполнено, если все величины  равномерно ограничены.

1. Можно обобщить эту теорему на случай слабо коррелированных величин . Если предположить, что коэффициент корреляции  (ясно, что всегда ) между  и  удовлетворяет неравенству  и что , то для нормальной устойчивости средних арифметических, т.е. для того, чтобы для всякого

,

достаточно выполнения условия , где .

2. В случае независимых слагаемых  можно дать также необходимое и достаточное условие для устойчивости средних арифметических .

Для каждого  существует константа  (медиана ), удовлетворяющая следующим условиям: , .

Положим

 

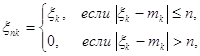
Теорема.

Пусть  – последовательность взаимно независимых случайных величин. Тогда условия

=, ,

,

необходимы и достаточны для устойчивости величин ,  При этом постоянные , , можно принять равными , так что в случае  (и только в этом случае) устойчивость нормальная.

Доказательство.

Достаточность условий теоремы устанавливается просто. В самом деле поскольку  а согласно неравенству Чебышева

 то

Для доказательства необходимости нам понадобится ряд вспомогательных предложений.

Лемма 1.

Пусть – независимые события, ,  и для некоторого . Если, кроме того, событие  таково, что для каждого , то тогда .

Доказательство.

Если существует такой номер , что , то .

Пусть теперь для всех  .

Тогда найдётся такое , что , и, значит, для всех

,

,

.

Отсюда

.

Что и требовалось доказать.

Лемма 2.

Пусть – независимые, ограниченные, , , случайные величины с нулевыми средними. Тогда для всякого  и целого

 , где .

Доказательство.

Пусть , , ,,

. Замечая, что на множестве  , получаем

 

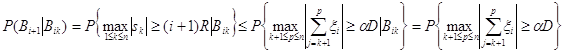
Из неравенства  следует, что

.

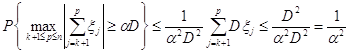Поэтому  при любом . Значит  и .

Что и требовалось доказать.

Лемма 3.

Пусть – независимые, ограниченные случайные величины, причём , . Тогда

.

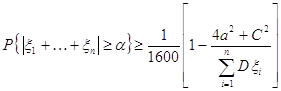Доказательство.

Обозначим , . Если  или , то правая часть в доказываемом неравенстве отрицательна и неравенство очевидно.

Пусть теперь одновременно , . Тогда достаточно показать, что , поскольку, очевидно,

.

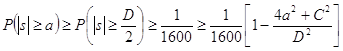Обозначим . Если , то

 и, значит,

Предположим, теперь, что .

Обозначая  и применяя лемму 2, находим

Отсюда

На множестве  .

Поэтому .

Ясно также, что .

Следовательно,

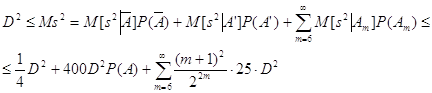
и, значит, .

Что и требовалось доказать.

Доказательство теоремы. Необходимость.

Пусть последовательность ,  такова, что для любого  , . Покажем, что тогда

, .

Обозначим для данного  , ,

.

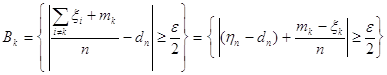Поскольку – медиана , то .

Для достаточно больших  , поэтому

, т.е. .

Далее, если событие  выполняется, а  нет, то выполняется событие  и, значит, .

Но .

Следовательно, .

Применим лемму 1, взяв .

Тогда .

События  независимы, поэтому .

Поскольку по условию , , то из  и  получаем искомое соотношение .

Положим теперь

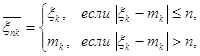
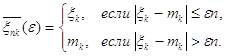
Из  следует, что если , , то и , .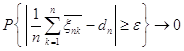

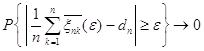Обозначим . Тогда  и по лемме 3

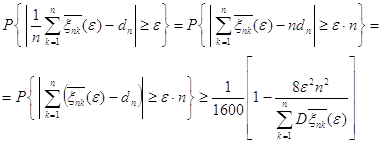
откуда .

Для  .

Тогда из ,

 и

 следует, что

, а значит в силу произвольности

.

Что и требовалось доказать.

3. Дальнейшее обобщение теоремы Чебышева получается, если предположить, что  каким-нибудь образом зависят от исходов каких-либо  испытаний , так что после каждого определённого исхода всех этих  испытаний  принимает определённое значение. Общая идея вех теорем, известных под названием закона больших чисел, состоит в том, что если зависимость величины  от каждого отдельного испытания , , очень мала при больших , то величины  устойчивы. Если рассматривать  как разумную меру зависимости величины  от испытания , то вышеупомянутая общая идея закона больших чисел может быть конкретизирована следующими рассуждениями.

Пусть .

Тогда ,

,

.

Легко, далее, подсчитать, что случайные величины , , некоррелированы. В самом деле, пусть , тогда, зная, что , можно записать следующее:

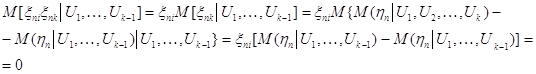
и, следовательно, , .

Итак, .

Таким образом, условие ,  достаточно для нормальной устойчивости величин .

Таким образом, была завершена одна из центральных проблем теории вероятностей – проблема закона больших чисел.

Заключение

Мы проследили динамику развития понятия вероятности; такого понятия в теории вероятностей, как математическое ожидание, а также развитие одной из центральных теорем–закона больших чисел. Можем сделать следующие выводы.

Проследив динамику развития и формирования понятия вероятности можно отметить, что оно вырабатывалось сложными путями. Понятие вероятности облекалось в определения различных форм и содержаний.

Вначале это понятие понимали на чисто интуитивном уровне. Позднее появились различные определения понятия вероятности. Наблюдались попытки вводить новые понятия, например «собственно вероятность», но эти попытки не увенчались успехом – это понятие не сохранилось в науке. В дальнейшем возникает необходимость в более чётком и строгом отношении к основным понятиям теории вероятностей, т.е. и к определению понятия вероятности. Этого требовало развитие статистической физики; этого требовало развитие самой теории вероятностей, в которой остро стала ощущаться неудовлетворённость классического обоснования лапласовского типа; этого требовало и развитие других наук, в которых широко применялись вероятностные понятия. Становилось всё отчётливее видно, что теория вероятностей нуждается в новом логическом обосновании – в обосновании с помощью аксиоматического метода. Многие учёные предпринимают попытки аксиоматического определения понятия вероятности. Однако успешно эта задача была решена в начале XX в. Колмогоровым. Аксиоматика Колмогорова способствовала тому, что теория вероятностей окончательно укрепилась как полноправная математическая дисциплина.

Развитие понятия математического ожидания также встречало ряд трудностей. Попытки ввести понятие морального ожидания, которое бы устраняло недостатки математического ожидания – провалились. Это произошло из-за того, что понятие морального ожидания не было связано с понятием вероятности в отличие от математического ожидания. В результате понятие «математическое ожидание» заняло прочное место, по праву ему принадлежащее, в теории вероятностей.

Динамику развития закона больших чисел можно сравнить с иерархической лестницей. В основании её простейшие теоремы Бернулли и Пуассона, а на вершине – критерий применимости закона больших чисел (необходимое и достаточное условия). В отличие от понятий вероятности и математического ожидания, закон больших чисел не сталкивался с подобными противоречиями, в своей трактовке. Усовершенствование закона больших чисел происходило плавно, без резких скачков.

Список источников

1. Майстров Л.Е. Теория вероятностей. Исторический очерк. – М.: Наука,

1967. – 320 с.

2    Майстров Л.Е. Развитие понятия вероятности. – М.: Наука, 1980. – 270 с.

3    Вентцель Е.С. Теория вероятностей. – М.: Наука. Главная редакция физ. – мат. литературы, 1969. – 576 с.

4    Гнеденко Б.В. Курс теории вероятностей. – М.: Наука. Главная редакция физ. – мат. литературы, 1969. – 400 с.

5    Колмогоров А.Н. Основные понятия теории вероятностей. – М.: Наука. Главная редакция физ. – мат. литературы, 1974. – 120 с.

6    История отечественной математики. В 4 т.–К.: Навукова думка, 1967. – Т.2.

7    Гливенко В.И. Курс теории вероятностей. – М.: Гостехиздат, 1939.

8    Чебышев П.Л. Полное собрание сочинений – М.–Л.: 1948.–Т.3.

9    История естествознания в России. – М.: 1960.–Т.2.

10  Гнеденко Б.В., Колмогоров А.Н. Теория вероятностей. – В кн.: «Математика в СССР за 30 лет». – М. – Л.: 1948.