Навигация
Качественное исследование построенных классов систем
2 Качественное исследование построенных классов систем
2.1 Исследование одной системы из первого класса построенных двумерных стационарных систем
Будем проводить исследование системы в предположении, что коэффициенты её определяются согласно формулам (1.17):
a= -![]() d, (1.17)
d, (1.17)
b=2d,
c=2a1(a1–1) d, d≠0, а1≠2,
с учётом в1=в2=с2=1 и предполагая, что параметр а1=1.
Тогда система (1.1) запишется в виде:
![]()
![]() dx+2dy+x2+2xy, (2.1)
dx+2dy+x2+2xy, (2.1)
![]() dy+2xy+y2
dy+2xy+y2
Интегральные кривые в этом случаи имеют вид:
y2–2xy+x2–2dy+2dx+d2=0, (2.2)
x–y+d=0.
При рассмотрении этого случая заметим, что интегральная кривая второго порядка y2–2xy+x2–2dy+2dx+d2=0 представляет собой две совпадающие прямые вида x–y+d=0, то есть:
(y–x)2–2d (y–x)+d2=0,
(y–x) – d)2=0,
y–x–d=0,
x–y+d=0.
Значит, если а1=в1=в2=с2=1 и если выполняются условия (1.17) система (1.1) имеет только один частный интеграл вида:
x–y+d=0. (2.3)
Найдём состояния равновесия системы (2.1). Приравняв правые части системы к нулю и, решив полученную систему, найдём точки покоя системы.
Система имеет четыре состояния равновесия:
О (0,0), А (-d, 0), B (-d, d), C(-![]() ).
).
Исследуем поведение траекторий в окрестностях состояний равновесия.
1. Исследуем точку О (0,0).
Составим характеристическое уравнение для точки имеет вид О (0,0):
![]() =0,
=0,
![]() 2=0.
2=0.
Характеристическими числами для точки О (0,0) системы (2.1) будут ![]()
Корни характеристического уравнения действительные, одного знака, но в зависимости от параметра d точка О (0,0) – устойчивый узел, если d<0; точка О (0,0) – неустойчивый узел, если d>0.
Из Главы 1. случай d=0 не рассматривается.
2. Исследуем точку А (-d, 0).
Составим характеристическое уравнение в точке А (-d, 0).
P (x, y)=dx+2dy+x2+2xy,
Q (x, y)=dy+2xy+y2.
Отсюда, получим:
Px=d+2x+2y, Py=2d+2x, (2.4)
Qx=2y,
Qy=d+2x+2y.
Следовательно, характеристическое уравнение примет вид:
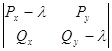 =0.
=0.
Итак, получаем:
![]() =0.
=0.
![]()
(–d–λ)2=0.
Характеристические числа для точки А (-d, 0) системы (2.1) будут ![]()
Корни λ1,λ2 – действительные, одного знака. В зависимости от параметра d.
Точка А (-d, 0) является неустойчивым узлом, если d<0; устойчивым узлом, если d>0.
3. Исследуем точку В (-d, d).
Составим характеристическое уравнение в точке В (-d, d).
Согласно равенствам (2.4) характеристическое уравнение примет вид:
![]() =0,
=0,
![]() 2=0,
2=0,
λ1=λ2=d.
λ1,λ2 – характеристические числа для точки В (-d, d) системы (2.4).
Корни λ1,λ2–действительные, одного знака зависящие от параметра d.
Если d<0, то точка В (-d, d) – устойчивый узел; если d>0, то точка В (-d, d) – неустойчивый узел.
4. Исследуем точку С(-![]() ).
).
Составим характеристическое уравнение в точке С(-![]() ).Применяя равенства (2.4), получим:
).Применяя равенства (2.4), получим:
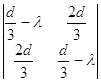 =0,
=0,
![]() .
.
Характеристические числа для точки С(-![]() ) системы (2.1) будут λ1=d, λ2=
) системы (2.1) будут λ1=d, λ2=![]() .
.
Корни λ1,λ2–действительные, различных знаков, независимо от параметра d.
Значит, точка С(-![]() ) – седло.
) – седло.
Исследуем бесконечно-удалённую часть плоскости на концах оси ОY. Преобразование x=![]() , y=
, y=![]() [1] переводит систему (2.1) в систему:
[1] переводит систему (2.1) в систему:
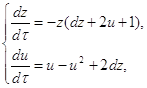 (2.5)
(2.5)
где t=zτ, dt=zdτ.
Для исследования состояний равновесий на концах оси ОУ, нам необходимо исследовать только точку No(0,0).Составим характеристическое уравнение в точке No (0,0):
![]() =0.
=0.
Получаем, что
![]()
Корни λ1,λ2–действительные и различных знаков не зависимо от параметра d. Значит, точка No(0,0) – седло.
Исследуем бесконечно-удалённую часть плоскости вне концов оси ОУ преобразованием [1] ![]() . Это преобразование систему (2.1) переводит в систему:
. Это преобразование систему (2.1) переводит в систему:
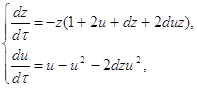 (2.6)
(2.6)
где t=zτ, dt=zdτ.
Изучим бесконечно-удалённые точки на оси U, то есть при z=0, получаем:
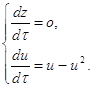
Следовательно, u1=0, u2=1.
Таким образом, получаем две точки N1(0,0), N2(0,1), которые являются состоянием равновесия. Исследуем характер этих точек обычным способом.
1. Исследуем точку N1(0,0).
Составляем характеристическое уравнение в точке N1(0,0):
![]() =0,
=0,
λ1=-1, λ2=1.
Корни λ1, λ2–действительные и различных знаков. Следовательно, точка N1(0,0) – седло.
2. Исследуем точку N2(0,1).
Составим характеристическое уравнение в точке N2(0,1):
Pz=–1–2u-2dz-4duz,
Pu=–2dz2–2z,
Qz=–2du2,
Qu=1–2u-4dzu.
Имеем:
![]() =0,
=0,
(-3–λ) (-1–λ)=0,
λ1=–3, λ2=–1,
Корни λ1,λ2–действительные и одного знака (–). Следовательно, точка N2(0,1) – устойчивый узел.
Дадим распределение состояний равновесия системы (2.1) в виде таблицы 1.
Таблица 1
| d | O (0,0) | A (-d, 0) | B (-d, d) | C( | ∞ | ||
| N0 | N1 | N2 | |||||
| (-∞; 0) | Уст.у. | Неуст.у. | Уст.у | Седло | Седло | Уст.у. | Седло |
| (0;∞) | Неуст.у. | Уст.у. | Неуст.у. | Седло | Седло | Уст.у. | Седло |
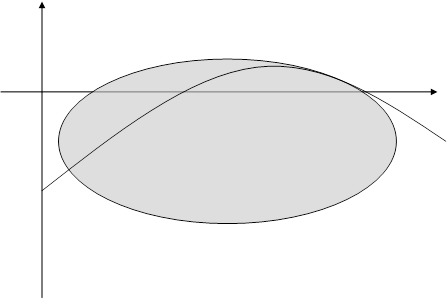
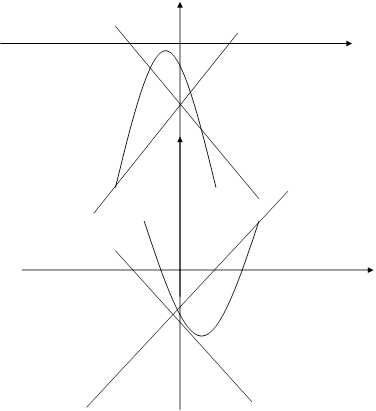
Положение кривой (2.3) и расположение относительно их состояний равновесия при d<0 и d>0 представлено на рис. 1 (а, б).
Поведение траекторий системы (2.1) в целом при d<0 и d>0 представлено на рис. 3 (а, б) приложения А.
Исследуя вид кривых (2.2) и расположение относительно их состояний равновесия, убеждаемся, что система (2.1) не имеет предельных циклов, так как Воробьёв А.П. [10] доказал, что для систем, правые части которых есть полиномы второй степени, предельный цикл может окружать только точку типа фокуса. Учитывая расположение состояний равновесия относительно кривых (2.2), являющиеся интегралами системы (2.1) не может существовать предельных циклов, окружающих несколько состояний равновесия.
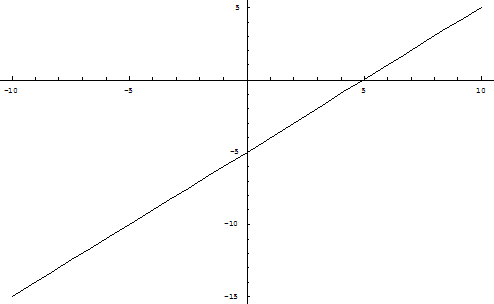
a) d<0
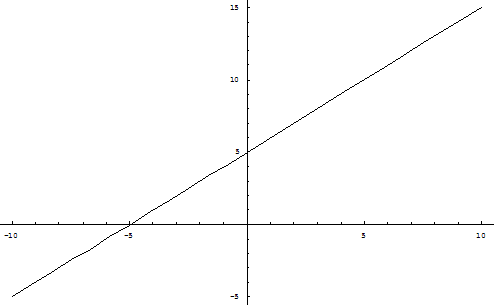
б) d>0
Рис. 1
Похожие работы
... (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
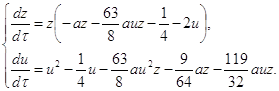
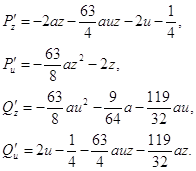
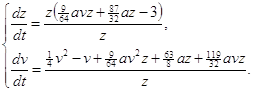
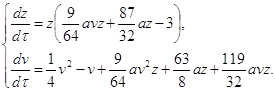
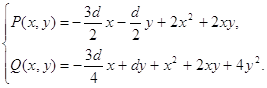
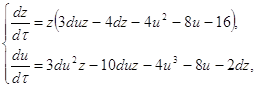










0 комментариев