Навигация
Исследование одной системы из второго класса построенных двумерных стационарных систем
2.2 Исследование одной системы из второго класса построенных двумерных стационарных систем
Рассмотрим систему (1.1) в предположении, что в1=в2=с2=1, а1=![]()
и коэффициенты определяются формулами (1.19). Тогда система (1.1) будет иметь вид:
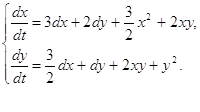 (2.7)
(2.7)
Интегральные кривые в этом случае имеют вид:
4y2–4xy+x2+dy=0, (2.8)
-![]() x+y=0. (2.9)
x+y=0. (2.9)
Найдём состояния равновесия системы (2.7). Для этого приравняем правые части системы нулю:

Решая эту систему, получим две пары точек, которые являются точками покоя системы (2.7): О (0,0), А(![]() ).
).
Исследуем поведение траекторий решений системы (2.7) в окрестностях состояний равновесия О (0,0), А(![]() ).
).
1. Исследуем точку О (0,0).
Составим характеристическое уравнение системы в точке О (0,0):
 =0,
=0,
![]() .
.
Характеристическими числами для точки О (0,0), будут ![]()
![]()
Так как один корень нулевой, тогда точка О (0,0) является сложным состоянием равновесия (изолированное состояние равновесия), для которого требуется дополнительное исследование. Для определения характера состояния равновесия О (0,0) воспользуемся теоремой [5].
Теорема 2.1 Пусть точка (0,0) – изолированное состояние равновесия системы:
![]()

где φ (x, y), ψ (x, y) – полиномы от x, y начиная со второй степени, y=φ(x) – решение уравнения y+Q2(x, y)=0, а разложение функции ψ(x)=P2(x, φ(x)) имеет вид:
![]()
Тогда:
1) при m-нечётном и ∆m>0 точка (0,0) – есть топологический узел;
2) при m-нечётном и ∆m<0 точка (0,0) – есть топологическое седло;
3) при m-чётном точка (0,0) есть седло-узел, то есть такое состояние равновесия, каноническая окрестность которого состоит из параболического и двух гиперболических секторов; При этом:
а) если ∆m<0, то внутри гиперболических
секторов заключён отрезок положительной
полуоси ОХ, примыкающий к точке (0,0);
б) если ∆m<0, то – отрезок отрицательной
полуоси ОХ.
Чтобы воспользоваться теоремой, необходимо систему (2.7) привести к виду:
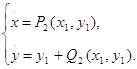 (2.10)
(2.10)
Это возможно сделать, воспользовавшись одним из следующих преобразований:
1. если в≠0, 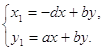
2. если в=0, а=0, 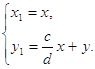
3. если в=0, d=0, 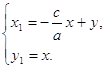
где а, в, с, d – коэффициенты системы (2.7).
Для системы (2.7) воспользуемся следующим преобразованием:
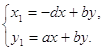
Получим:
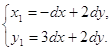
Откуда:
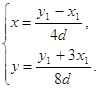
Следовательно, можем найти:
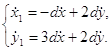
Тогда:
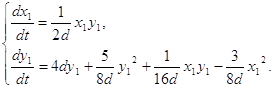
Чтобы данную систему привести к системе вида (2.10), сделаем замену ![]() тогда dt=
тогда dt=![]() dh и получим систему:
dh и получим систему:
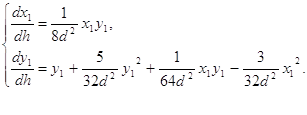
Найдём решение уравнения:
y1+![]() (2.11)
(2.11)
в виде ряда по степеням y1:
y1=φ(x1)=c1x1+c2x12+….
Подставим y1=c1x1+c2x12+… в уравнение (2.11), получим:
c1x1+c2x12+ … +![]() (c1x1+c2x12+…)2+
(c1x1+c2x12+…)2+![]() x1(c1x1+c2x12+…)–
x1(c1x1+c2x12+…)–![]() x12=0.
x12=0.
x11: ![]() с1=0,
с1=0,
x12: с2+![]() с1+
с1+![]() с1
с1![]() =0,
=0,
Следовательно с1=0, с2=![]() , ….
, ….
Тогда y1=φ(x1)= ![]() х12+….
х12+….
Находим ψ(х1)=Р2(х1,φ(х1))=![]() (
(![]()
![]() +……)=
+……)=![]() +……..=∆mxm.
+……..=∆mxm.
Получили m=3-нечётное, ∆m>0.
Следовательно, по теореме 2.1 получаем, что точка О (0,0) – топологический узел.
2. Исследуем точку А(![]() ).
).
Составим характеристическое уравнение в точке А(![]() ).
).
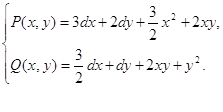
Отсюда
Px(x, y)=3d+3x+2y,
Py(x, y)=2d+2x,
Qx(x, y)=![]() d+2y,
d+2y,
Qy(x, y)=d+2x+2y.
Следовательно, характеристическое уравнение имеет вид:
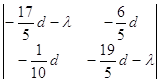 =0.
=0.
Характеристическими числами для точки А(![]() ) системы (2.7) будут λ1=–4d, λ2=
) системы (2.7) будут λ1=–4d, λ2=![]() d.
d.
Корни λ1, λ2–действительные и одного знака, зависящие от параметра d. Если d<0, тогда точка А(![]() ) – неустойчивый узел; если d>0, тогда точка А(
) – неустойчивый узел; если d>0, тогда точка А(![]() ) – устойчивый узел.
) – устойчивый узел.
Исследуем бесконечно-удалённую часть плоскости системы (2.7) вне концов оси ОУ. Преобразование [1] ![]() переводит систему (2.7) в систему:
переводит систему (2.7) в систему:
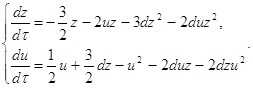 (2.12)
(2.12)
где t=zτ, dt=zdτ.
Изучим бесконечно-удалённые точки на оси U, то есть z=0. Получаем:
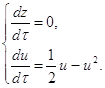
Следовательно, ![]() u1=0, u2=
u1=0, u2=![]() .
.
Таким образом, получили две точки N1(0,0), N2(0,![]() ), которые являются состояниями равновесия. Исследуем характер этих точек обычным способом.
), которые являются состояниями равновесия. Исследуем характер этих точек обычным способом.
1. Исследуем точку N1(0,0).
Составим характеристическое уравнение в точке N1(0,0):
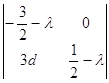 =0,
=0,
λ1= ![]() , λ2=
, λ2=![]() .
.
Корни λ1,λ2–действительные и различных знаков, следовательно, точка N1(0,0) – седло.
2. Исследуем точку N2(0,![]() ).
).
Составим характеристическое уравнение в точке N2(0,![]() ):
):
Pz=![]() –2u-6dz-4duz,
–2u-6dz-4duz,
Pu=–2z-2dz2,
Qz=![]() d-2du-2du2,
d-2du-2du2,
Qu=![]() –2u-2dz-4duz.
–2u-2dz-4duz.
Характеристическое уравнение имеет вид:
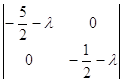 =0.
=0.
Следовательно, характеристические числа:
λ1=![]() , λ2=
, λ2=![]() .
.
Корни λ1,λ2–действительные, различных знаков, значит точка N2(0,![]() ) является седлом.
) является седлом.
Исследуем бесконечно-удалённые концы оси ОУ с помощью преобразования [1] x=![]() , y=
, y=![]() .Это преобразование переводит (2.7) в систему:
.Это преобразование переводит (2.7) в систему:
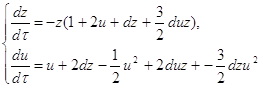
где t=zτ, dt=zdτ.
Для исследования состояний равновесия на концах оси ОУ, нам необходимо исследовать только точку (0,0), которая является состоянием равновесия данной системы. Составим характеристическое уравнение в точке (0,0):
![]() =0.
=0.
![]()
Корни λ1,λ2–действительные и различных знаков, значит точка (0,0) – седло.
Теперь дадим распределение состояний равновесия системы (2.7) в виде таблицы 2.
Таблица 2
| d | O (0,0) | A( | ∞ | ||
| N0 | N1 | N2 | |||
| (-∞; 0) | Топологическое Узел | Неустойчивый Узел | Седло | Устойчивый Узел | Седло |
| (0;∞) | Топологическое Узел | Устойчивый Узел | Седло | Устойчивый Узел | Седло |
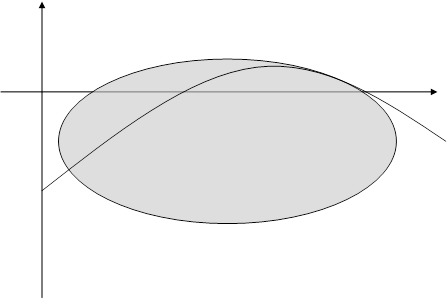
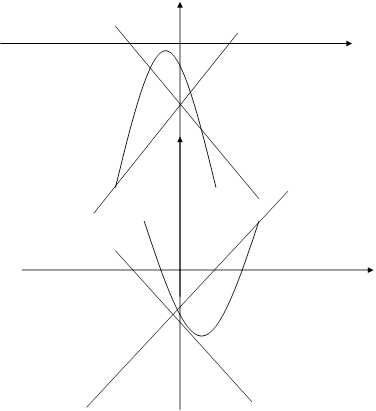
Положение кривых (2.8), (2.9) и расположение относительно их состояний равновесия при d<0 и d>0 даётся соответственно рис. 2 (а, б).
Поведение траекторий системы (2.7) в целом при d<0, d>0 представлено на рис. 4 (а, б) приложения Б.
Так как Воробьёв А.П. [10] доказал, что для систем, правые части которых есть полиномы второй степени, предельный цикл может окружать только точку типа фокуса, тогда исследуя вид кривых (2.8), (2.9) и расположение относительно их состояний равновесия, убеждаемся, что система (2.7) не имеет предельных циклов.
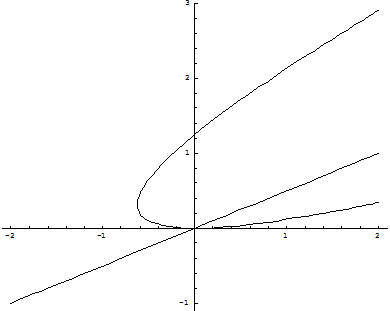
a) d<0
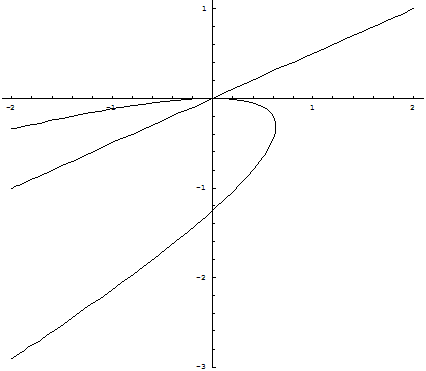
б) d>0
Рис. 2
Заключение
В данной дипломной работе построены два класса квадратичных двумерных стационарных систем при условии, что частными интегралами являются кривые второго и первого порядков. При этом коэффициенты кривых выражаются через произвольные параметры систем.
Проведено качественное исследование построенных классов систем при фиксированном значении одного из параметров системы. Выведены необходимые и достаточные условия существования у системы двух частных интегралов. В зависимости от условий на коэффициенты были рассмотрены два случая. Найдены состояния равновесия полученных систем, которые принадлежат интегральным кривым. Исследована бесконечно-удалённая часть плоскости систем и доказано отсутствие предельных циклов. Построена качественная картина поведения траекторий систем в круге Пуанкаре.
Список источников
1 Пуанкаре А. О кривых, определяемых дифференциальными уравнениями.-М.-Л.: ГИТТЛ, 1947. – 839 с.
2 Бендиксон И. О кривых, определяемых дифференциальными уравнениями. – УМН, 1941. – Вып. 9. – 643 с.
3 Биркгоф Дж.Д. Динамические системы. М.-Л.: Гостехиздат, 1941. – 340 с.
4 Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую. – ПММ. – 1952. – Т.16, Вып. 6. – с. 659–670.
5 Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. - М.: Наука, 1976. – 274 с.
6 Серебрякова Н.Н. Качественное исследование одной системы дифференциальных уравнений теории колебаний. – ПММ. – 1963 Т.27, Вып. 1. – 230 с.
7 Черкас Л.А. Об алгебраических решениях уравнения ![]() , где P и Q – многочлены второй степени // ДАН БССР. – 1963. – Т.7, №11. – 950 с.
, где P и Q – многочлены второй степени // ДАН БССР. – 1963. – Т.7, №11. – 950 с.
8 Яблонский А.И. Алгебраические интегралы одной системы дифференциальных уравнений // Дифференц. уравнения. – 1970. – Т.6, №10. – с. 1752–1760.
9 Филипцов В.Ф. К вопросу алгебраических интегралов одной системы дифференциальных уравнений // Дифференц. уравнения. – 1973. – Т.9, №3. – 256 с.
10 Воробьев А.П. К вопросу о циклах вокруг особой точки типа "узел" // ДАН БССР. – 1960. – Т.4, №9. – 720 с.
Похожие работы
... (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
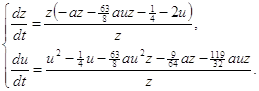
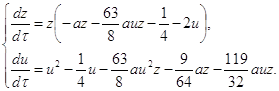
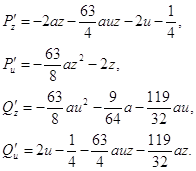
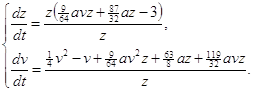
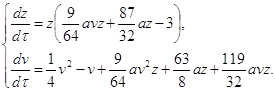
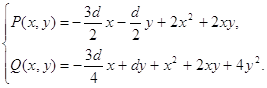
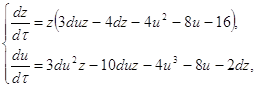










0 комментариев