Определение вида прогнозной модели. Линеаризация тренда

2.2.7 Определение вида прогнозной модели. Линеаризация тренда

Зависимость f(t) выявляется с помощью процедуры экстраполяции тенденций исследуемого процесса, заключающейся в подборе теоретической кривой, адекватно описывающей процесс изменения показателя.

Экстраполяция ряда выполняется с помощью математических функций, которые подбираются под эмпирическую совокупность статистических данных. Эта функция позволяет получить расчетные значения уровней ряда, т. е. значения, которые наблюдались бы при полном совпадении теоретической кривой с фактическими значениями ряда.

Экстраполяция тенденции временного ряда осуществляется в два этапа:

•выбор типа кривой, форма которой соответствует характеру тенденции временного ряда;

•определение численных значений параметров кривой.

Выбор типа кривой (основной этап при экстраполяции тенденций ряда. Это достаточно трудоемкий процесс, ибо перебор различных видов функциональных зависимостей осуществляется в обширном классе аналитических функций. В практике экстраполяции тенденции временных рядов наиболее часто встречаются следующие зависимости (рис.2.9):

1)линейная функция: х = a + bt;

2)парабола: х = а + bt + ct²;

3)полином третьей степени: х = а + bt + ct² + dt³;

4)гипербола: х = а +

5)степенная функция: х = аt^b

6) экспоненциальная функция: х = ае^bt ;

⁷⁾   модифицированная экспонента: x=k - ае^bt ;

8)экспоненциально-степенная функция: х = e^att^b;

9)логистическая (S – образная ) функция: x = k (1+be^-at) ;

10)функция Гомпертца: x = ka^bt;

11)квадратная логистическая функция: ;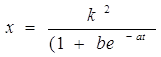

12)логарифмическая функция: x = b lgt.

При экстраполяции тенденций ряда задача состоит в том, чтобы определить параметры выбранной функции a₀, a₁, а₂ и т. д. Для определения этих параметров применяют метод наименьших квадратов.

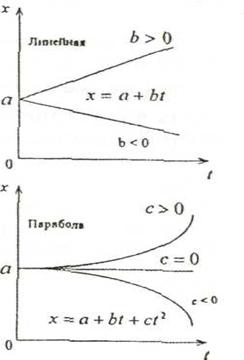
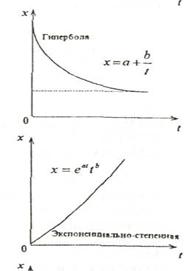
рис. 2.9. – Общий вид некоторых прогнозных кривых

2.2.8 Предварительная обработка прогнозной информации

При значительном разбросе значении исходного ряда для облегчения процедуры выбора типа кривой и уменьшения трудоемкости се математического описания осуществляют предварительную обработку исходного числового ряда путем его сглаживания и выравнивания.

Процедуру сглаживания применяют в целях уменьшения случайных отклонений единичных значений числового ряда, как правило, методом скользящей средней. Для этого определяют средние значения групп точек исходного ряда, при этом группы выбирают как бы скользящими от начала к концу ряда. Так, к примеру, при сглаживании группы по пяти значениям, имеем группы:

…

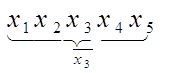
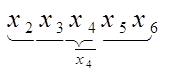
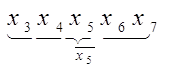Остающиеся крайние точки (х₁, х₂ и x_n-1, x_n) сглаживают по специальным формулам.

Для сглаживания по трем точкам применяют формулы:

;

;

,

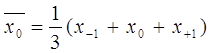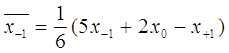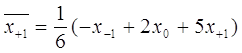где х₀,  — исходное и сглаженное значения средней точки в скользящей группе; х_-1,  — исходное и сглаженное значения в левой от средней точке; х₊₁,  — исходное и сглаженное значения в правой от средней точке.

Для средней точки скользящей группы из т = 2к +1 точек в общем виде формула имеет вид

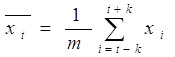
При большом числе точек исходного ряда используют рекуррентную формулу:

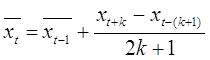
При наличии в исходном ряде значительных случайных отклонений единичных реализаций от групповых средних процедура сглаживания дает хорошие результаты, способствуя выявлению тенденции ряда. При необходимости сглаживание может быть выполнено повторно по уже сглаженному ряду значений. Однако эффективность многократного сглаживания быстро уменьшается и более одного — трех раз его выполнять нецелесообразно.

Метод наименьших квадратов дает наиболее точные результаты при аппроксимации линейных зависимостей. Достаточно успешно его применяют также для определения параметров парабол, кубических полиномов и гипербол. Чтобы получить параметры других аппроксимирующих зависимостей, прибегают к процедуре выравнивания тренда путем его линеаризации. То есть эмпирическую зависимость вида x = f(t) приводят к виду

X=A+BT.

Коэффициенты А и В линеаризованной зависимости определяют методом наименьших квадратов, после чего осуществляют обратный переход от вычисленных значений А и В к исходным a и b произвольной функции x = f(t).