Просмотр сетевого графика ведётся от его начального события к конечному;

1        Просмотр сетевого графика ведётся от его начального события к конечному;

2        При рассмотрении начального события сетевого графика, в качестве работы, лежащей на критическом пути, выбирается та, которая имеет нулевой полный резерв времени. В соответствии с теоремой 3.1 (утверждение-необходимость), такая работа обязательно будет существовать;

3        При рассмотрении работ, исходящих из события, к которому привила работа с нулевым полным резервом времени, выбирается работа, также имеющая нулевой полный резерв времени. В соответствии с теоремой 3.2, такая работа существует;

4        Если, среди исходящих из некоторого события работ, есть несколько работ с нулевыми полными резервами времени, то выбирается любая. При этом, согласно теореме 3.2, процесс построения критического пути в тупик зайти не может, и рано или поздно дойдет до завершающего события сетевого графика.

Реализация указанных правил даёт путь, состоящий только из работ с нулевыми полными резервами времени. Тогда, на основании теоремы 3.1 (утверждение-достаточность), этот путь и будет являться критическим.

В целях проверки, доказанная методика применена для сетевого графика, представленного на рисунке 2.1 . Здесь, найденные критические пути, выделены жирными стрелками. Как видно, таких путей два, благодаря тому, что среди работ, исходящих из события 0, есть две работы с нулевыми полными резервами времени. Проверить то, что найденные пути являются критическими легко, просуммировав длительности принадлежащих им работ. Суммы окажутся: во-первых, равными между собой, а во-вторых, наибольшими среди аналогичных сумм других возможных путей.

Теперь рассмотрим вопрос поиска наикратчайшего пути сетевого графика. Оказывается, для его поиска можно применять, методику поиска критического пути, если использовать идею, высказываемую в следующей теореме.

Теорема 3.3 – Если произвести расчёт параметров заданного сетевого графика по установленным правилам, но заменяя известные длительности работ на те же значения с отрицательным знаком (длительности всех работ будут меньше нуля), то наикратчайший путь сетевого графика станет подчиняться всем свойствам критического пути.

Эту теорему легко доказать, используя правило сравнения отрицательных чисел. Данное правило заключается в том, что одно отрицательное число считается большим другого, если абсолютное значение первого меньше абсолютного значения второго. Поскольку длительность наикратчайшего пути, по абсолютному значению наименьшая, среди длительностей всех других путей сетевого графика, то, на основании указанного правила, отрицательная длительность наикратчайшего пути будет наибольшей среди отрицательных длительностей остальных путей. Тогда, наикратчайший путь, состоящий из работ с отрицательными длительностями, будет критическим, при условии, что все остальные пути, также состоят из работ с отрицательными длительностями. Теорема доказана.

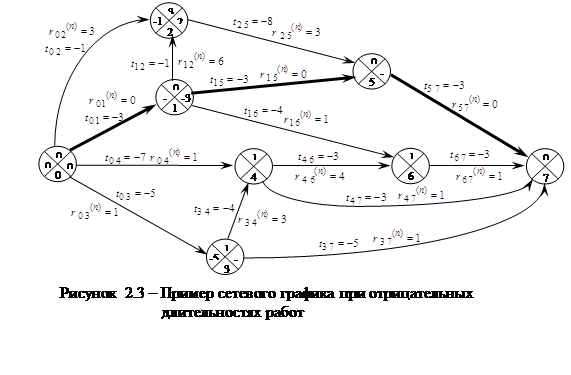
Для проверки доказанной теоремы, параметры сетевого графика на рисунке 2.1 пересчитаны заново, при отрицательных значениях длительностей работ, и представлены на рисунке 2.3. Как видно, сетевой график на рисунке2.3 содержит путь, работы которого имеют только нулевые полные резервы времени. Данный путь выделен жирными стрелками. Этот путь, являясь критическим для сетевого графика на рисунке 2.3, в тоже время является наикратчайшим путем для сетевого графика на рисунке 2.1 . Последнее можно проверить простым суммированием длительностей его работ. Полученная сумма должна быть наименьшей по абсолютному значению, среди аналогичных сумм других путей сетевого графика на рисунке 2.1 .

Вообще говоря, для нахождения продолжительности наикратчайшего пути, необходимой при анализе оптимальности сетевого графика по критерию (1.1), не обязательно суммировать длительности всех, принадлежащих ему работ. Она уже известна из рассчитанных, при отрицательных длительностях работ, параметров сетевого графика, и равна, как и для любого критического пути, сроку свершения завершающего события. Естественно, что данный срок свершения имеет отрицательное значение, и поэтому, для нахождения фактической длительности наикратчайшего пути, требуется менять это значение на противоположное.

Необходимо сказать, что можно поставить и решить общую задачу поиска пути заданной продолжительности. Но данная задача принципиальной важности, при анализе сетевого графика, не несёт. Для анализа оптимальности сетевого графика и осуществления его оптимизации, достаточно знать лишь, как проходят особые пути, и какова их продолжительность.

Рынок технических устройств аналогичного характера представлен: частными фирмами, конструкторскими бюро, лабораториями, организованными на базе НИИ, НПО, занимающимися передовыми и прибыльными разработками на уровне мировых стандартов.

Данная группа производителей способна разрабатывать и выпускать любые партии изделий высокого качества, использую передовые технологии и материальную базу. Эта группа активно отслеживает конъюнктуру рынка и гибко реагирует на его потребности.

Другая группа производителей - это иностранные фирмы, имеющие свои представительства в нашей стране. Их продукцию отличает высокое качество, надёжность и потребительские характеристики. Цены иностранных производителей всегда выше отечественных, а вследствие постоянного падения курса отечественной валюты, цена будет постоянно расти. Такие фирмы не могут конкурировать с другими группами рынка из-за слишком высокой цены на свою продукцию.

Спрос на устройства аналогичной группы достаточно высок. По способу использования аппаратуры он разделяется на коммерческий и бытовой. Спрос на аппаратуру для коммерческого использования прежде всего определяется качеством продукта, поэтому производителями являются фирмы, обладающие высокотехнологичным производством и современным исследовательским комплексом. Спрос на аппаратуру для бытового использования в основном определяется ценой.

Прогнозируя развитие рынка сбыта на будущее, можно предположить переключение спроса с дорогой импортной аппаратуры на аппаратуру отечественного производства того же класса. Ситуация усугубляется предполагаемой высокой инфляцией. Прогнозируемый объём продаж составит до нескольких тысяч штук в год.

Для обеспечения прогнозируемого сбыта разрабатываемого устройства необходимо проведение ряда мер:

1) маркетинговые мероприятия, то есть проведение рекламной деятельности по сбыту: участие в специализированных выставках, издание рекламной литературы для специалистов и физических лиц, установление контактов с потребителями;

2) калькуляция затрат для получения возможности снижения цены путём сокращения определённых статей расходов, повышая этим конкурентоспособность;

3) послепродажное обслуживание, т. е. организация центров гарантийного и послегарантийного обслуживания.

Многие крупные проекты, такие как строительство дома, изготовление станка, разработка автоматизированной системы бухгалтерского учета и т.д., можно разбить на большое количество различных операций (работ). Некоторые из этих операций могут выполняться одновременно, другие — только последовательно: одна операция после окончания другой. Например, при строительстве дома можно совместить во времени внутренние отделочные работы и работы по благоустройству территории, однако возводить стены можно только после того, как будет готов фундамент.

Задачи планирования работ по осуществлению некоторого проекта состоят в определении времени возможного окончания как всего проекта в целом, так и отдельных работ, образующих проект; в определении резервов времени для выполнения отдельных работ; в определении критических работ, то есть таких работ, задержка в выполнении которых ведет к задержке выполнения всего проекта в целом; в управлении ресурсами, если таковые имеются и т.п.

Для организации разработки большое распространение получил метод сетевого планирования и управления.

Для выполнения работ по заданной теме сетевая модель разбивается на отдельные чётко определенные работы и отражает логическую взаимосвязь и параметры всех работ и событий разработки.

Планирование работ с применением сетевого метода осуществляется в следующей последовательности:

1)              составление перечня всех работ,

2)              определение продолжительности работ,

3)              составление сетевого графика,

4)              расчёт основных параметров сетевого графика,

5)              определение критического пути,

6)              анализ сетевого графика и его оптимизация.

Для построения сетевого графика необходимо составить таблицу с перечнем всех событий и работ. Для оценки продолжительности работ применяется вероятностный принцип, при этом ответственный представитель по каждой работе делает две оценки и, на основе этих оценок, определяет ожидаемое время по формуле:

 (2.13)

t_min – минимальная продолжительность работы при благоприятных условиях;

t_max – максимальная продолжительность работы при неблагоприятных условиях.