Навигация
Прогнозирование временных рядов с использованием метода авторегрессии
2.2.12 Прогнозирование временных рядов с использованием метода авторегрессии
При сглаживании и прогнозировании временных рядов рассмотренными выше методами для расчета прогноза использовался только тренд, т. е. детерминированная составляющая процесса. Однако для решения практических задач невозможно получить такой тренд, который позволил бы добиться максимального совпадения расчетных и фактических значений показателей, т. е. нет возможности получить такие значения коэффициентов аi, которые обратили бы в нуль сумму Q или придали бы ей значение, близкое к нулю.
Уровень погрешности можно снизить путем прогнозирования случайной компоненты εt. Тогда прогноз показателя будет суммой прогнозов детерминированной и случайной составляющих:
xt = f(t) + ε*t + ut (2.25)
Здесь xt — временной ряд;
f(t) — тренд временного ряда;
ε*t — прогноз отклонения случайной компоненты εt ;
ut— ошибка протезирования εt.
Если случайная величина εt распределена по нормальному закону, для ее прогнозирования применяют метод авторегрессии.
Процессом авторегрессии называется процесс, значения которого в последующие моменты времени зависят от его значений в предшествующие моменты времени:
![]() (2.26)
(2.26)
где коэффициенты β1, β2, …, βр-1, βр — коэффициенты уравнения авторегрессии; иt — ошибка авторегрессии.
Расчет коэффициентов авторегрессии β1, β2, …, βр-1, βр производится методом наименьших квадратов из условия минимума дисперсии склонений в фиксированной выборке из п наблюдений:
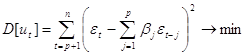
Это условие приводит к системе нормальных уравнений:
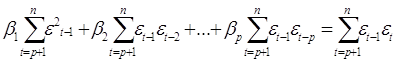
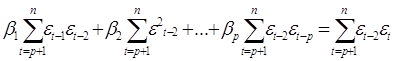
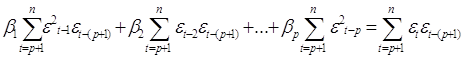
Число переменных, входящих в модель авторегрессии, называется порядком авторегрессии. В (2.26) приведена модель авторегрессии р-ro порядка.
Определение порядка авторегрессии является одним из наиболее ответственных этапов построения авторегрессионной модели. Для этого привлекают довольно громоздкий математический аппарат. Но в практических расчетах порядок авторегрессии обычно определяют эмпирическим путем. Построив несколько моделей разного порядка, проверяют точность прогноза на ретроспективных данных и на основе анализа полученных результатов делают вывод о порядке авторегрессии.
2.2.13 Прогнозирование временных рядов методов огибающих кривых
Многие динамические ряды при существенном изменении независимой переменной — времени — проявляют тенденцию к насыщению, т. е. при росте t зависимый показатель приближается к некоторой асимптоте — своему предельному значению. Такое поведение динамического ряда имеет вполне определенный физический смысл: происходит стабилизация прогнозируемого признака. В историческом аспекте насыщение динамического ряда означает подготовку смены технических и технологических формаций.
Традиционный подход к прогнозированию насыщающихся процессов основываемся на предположении, что экспериментальный динамический ряд насыщающегося процесса описывается по закону логистической кривой. Уравнение логистической кривой имеет вид
П(t) = k(1+be-ct), (2.27)
где П(t) — прогнозируемый показатель; t — время протекания процесса, характеризующегося показателем П(t) ; k, b, c — коэффициенты;
П(t)
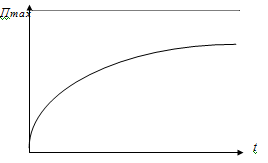
рис.2.11Кривая насыщения П(t)
е — основание натуральных логарифмов; Пmax — предельное значение (асимптота) функции П(t).
Логистическая кривая описывает изменение главного признака на одном из исторических этапов. Таких этапов может быть несколько, при этом для каждого из них существует своя логистическая или близкая к ней (рис. 2.11) кривая насыщения. Можно ожидать, что огибающие кривые будут принимать форму большой S-образной кривой, описанной вокруг малых 5-образных кривых, характеризующих конкретные этапы (рис. 2.12).
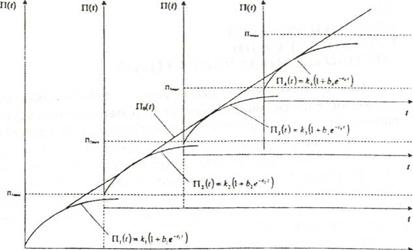
рис. 2.12 Огибающая По(t) семейства логистических кривых насыщения П(t)
2.2.14 Выбор метода прогнозирования
Прогнозирование на основе анализа временных рядов предполагает, что происходившие изменения в объемах продаж могут быть использованы для определения этого показателя в последующие периоды времени. Временные ряды, подобные тем, что приведены в таблице 2.11, обычно служат для расчета четырех различных типов изменений в показателях: трендовых, сезонных, циклических и случайных.
Таблица 2.11
Ежемесячное производство телег, шт
| Месяц | 2004 | 2005 | 2006 | 2007 |
| Январь | 9 | 30 | 28 | 29 |
| Февраль | 10 | 28 | 30 | 35 |
| Март | 15 | 25 | 29 | 30 |
| Апрель | 13 | 32 | 27 | 28 |
| Май | 19 | 34 | 26 | 22 |
| Июнь | 20 | 27 | 25 | 26 |
| Июль | 13 | 28 | 30 | 32 |
| Август | 20 | 30 | 31 | 25 |
| Сентябрь | 25 | 29 | 32 | 29 |
| Октябрь | 26 | 32 | 33 | 30 |
| Ноябрь | 28 | 31 | 26 | 30 |
| Декабрь | 32 | 33 | 28 | 30 |
Тренд– это изменение, определяющее общее направление развития, основную тенденцию временных рядов. Выявление основной тенденции развития (тренда) называется выравниванием временного ряда, а методы выявления основной тенденции– методами выравнивания.
Один из наиболее простых приемов обнаружения общей тенденции развития явления– укрупнение интервала динамического ряда. Смысл этого приема заключается в том, что первоначальный ряд динамики преобразуется и заменяется другим, уровни которого относятся к большим по продолжительности периодам времени. Так, например, месячные данные таб.2.11 могут быть преобразованы в ряд годовых данных. График ежегодного производства, приведенный на рис.2.13, показывает, что потребление возрастает из года в год в течение исследуемого периода. Тренд в потреблении является характеристикой относительно стабильного темпа роста показателя за период.
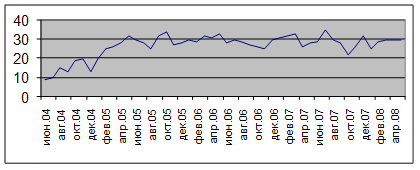
Рис. 2.13 Ежемесячное потребление телег в 2006—2008 гг.
Выявление основной тенденции может быть осуществлено также методом скользящей средней. Для определения скользящей средней формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно передвигаясь от начального уровня динамического ряда на одно значение. По сформированным укрупненным данным рассчитываем скользящие средние, которые относятся к середине укрупненного интервала.
Прогнозирование на основе анализа временных рядов предполагает, что происходившие изменения в объемах продаж могут быть использованы для определения этого показателя в последующие периоды времени. Временные ряды, подобные тем, что приведены в таблице 2.11, обычно служат для расчета четырех различных типов изменений в показателях.
Выявление основной тенденции может быть осуществлено также методом скользящей средней. Для определения скользящей средней формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно передвигаясь от начального уровня динамического ряда на одно значение. По сформированным укрупненным данным рассчитываем скользящие средние, которые относятся к середине укрупненного интервала.
Порядок расчета скользящих средних по потреблению телег в 2006-2008 гг. приведен в таблице2.12.
Таблица 2.12 Расчет скользящих средних по данным за 2004-2007 гг
| t | Месяц | Количество | Скользящее среднее |
| 1 | Июнь 2004 | 9 | #Н/Д |
| 2 | Июль 2004 | 10 | #Н/Д |
| 3 | Август 2004 | 15 | 11,33 |
| 4 | Сентябрь 2004 | 13 | 12,67 |
| 5 | Октябрь 2004 | 19 | 15,67 |
| 6 | Ноябрь 2004 | 20 | 17,33 |
| 7 | Декабрь 2004 | 13 | 17,33 |
| 8 | Январь 2005 | 20 | 17,67 |
| 9 | Февраль 2005 | 25 | 19,33 |
| 10 | Март 2005 | 26 | 23,67 |
| 11 | Апрель 2005 | 28 | 26,33 |
| 12 | Май 2005 | 32 | 28,67 |
| 13 | Июнь 2005 | 30 | 30,00 |
| 14 | Июль 2005 | 28 | 30,00 |
| 15 | Август 2005 | 25 | 27,67 |
| 16 | Сентябрь 2005 | 32 | 28,33 |
| 17 | Октябрь 2005 | 34 | 30,33 |
| 18 | Ноябрь 2005 | 27 | 31,00 |
| 19 | Декабрь 2005 | 28 | 29,67 |
| 20 | Январь 2006 | 30 | 28,33 |
| 21 | Февраль 2006 | 29 | 29,00 |
| 22 | Март 2006 | 32 | 30,33 |
| 23 | Апрель 2006 | 31 | 30,67 |
| 24 | Май 2006 | 33 | 32,00 |
| 25 | Июнь 2006 | 28 | 30,67 |
| 26 | Июль 2006 | 30 | 30,33 |
| 27 | Август 2006 | 29 | 29,00 |
| 28 | Сентябрь 2006 | 27 | 28,67 |
| 29 | Октябрь 2006 | 26 | 27,33 |
| 30 | Ноябрь 2006 | 25 | 26,00 |
| 31 | Декабрь 2006 | 30 | 27,00 |
| 32 | Январь 2007 | 31 | 28,67 |
| 33 | Февраль 2007 | 32 | 31,00 |
| 34 | Март 2007 | 33 | 32,00 |
| 35 | Апрель 2007 | 26 | 30,33 |
| 36 | Май 2007 | 28 | 29,00 |
| 37 | Июнь 2007 | 29 | 27,67 |
| 38 | Июль 2007 | 35 | 30,67 |
| 39 | Август 2007 | 30 | 31,33 |
| 40 | Сентябрь 2007 | 28 | 31,00 |
| 41 | Октябрь 2007 | 22 | 26,67 |
| 42 | Ноябрь 2007 | 26 | 25,33 |
| 43 | Декабрь 2007 | 32 | 26,67 |
| 44 | Январь 2008 | 25 | 27,67 |
| 45 | Февраль 2008 | 29 | 28,67 |
| 46 | Март 2008 | 30 | 28,00 |
| 47 | Апрель 2008 | 30 | 29,67 |
| 48 | Май 2008 | 30 | 30,00 |
Изучение основной тенденции развития методом скользящей средней является эмпирическим приемом предварительного анализа. Для того чтобы дать количественную модель изменений динамического ряда, используется метод аналитического выравнивания. В этом случае фактические уровни ряда заменяются теоретическими, рассчитанными по определенной кривой, отражающей общую тенденцию изменения показателей во времени. Таким образом, уровни динамического ряда рассматриваются как функция времени:
![]()
Наиболее часто могут использоваться следующие функции:
1) при равномерном развитии– линейная функция: ![]() ;
;
2) при росте с ускорением:
a) парабола второго порядка: ![]() ;
;
b) кубическая парабола: ![]() ;
;
3) при постоянных темпах роста– показательная функция: ![]() ;
;
4) при снижении с замедлением– гиперболическая функция: ![]() .
.
Однако аналитическое выравнивание содержит в себе ряд условностей: развитие явлений обусловлено не только тем, сколько времени прошло с отправного момента, а и тем, какие силы влияли на развитие, в каком направлении и с какой интенсивностью. Развитие явлений во времени выступает как внешнее выражение этих сил.
Оценки параметров ![]() находятся методом наименьших квадратов, сущность которого состоит в отыскании таких параметров, при которых сумма квадратов отклонений расчетных значений уровней, вычисленных по искомой формуле, от их фактических значений была бы минимальной.
находятся методом наименьших квадратов, сущность которого состоит в отыскании таких параметров, при которых сумма квадратов отклонений расчетных значений уровней, вычисленных по искомой формуле, от их фактических значений была бы минимальной.
Для сглаживания экономических временных рядов нецелесообразно использовать функции, содержащие большое количество параметров, так как полученные таким образом уравнения тренда (особенно при малом числе наблюдений) будут отражать случайные колебания, а не основную тенденцию развития явления.
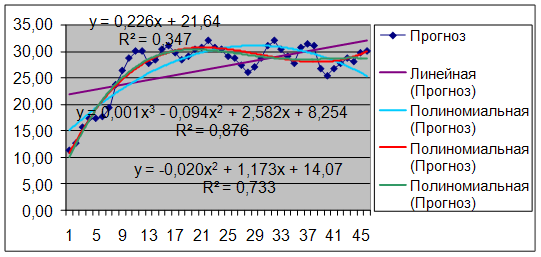
рис.2.14 – скользящее среднее
Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки.
Выбираем тренд с наименьшей дисперсией остатков s2. Это полиномиальный тренд 3-го порядка, где остаток составляет 14,07.
1. По выбранному тренду составить прогноз для t=T+1,T+2,T+3 и т.д, где T=48 – последний член временного ряда в таблице. Прогноз вычисляется по формулам:
![]() =a0+a1(T+1)+a2(T+1)2+a3(T+1)3,
=a0+a1(T+1)+a2(T+1)2+a3(T+1)3,
![]() = a0+a1(T+2)+a2(T+2)2+a3(T+2)3,
= a0+a1(T+2)+a2(T+2)2+a3(T+2)3,
![]() = a0+a1(T+3)+a2(T+3)2+a3(T+3)3,
= a0+a1(T+3)+a2(T+3)2+a3(T+3)3,
где ai , i=1,2,3-оценки коэффициентов выбранного полиномиального тренда.
2. Вычислить доверительный интервал для прогнозов по формулам:
![]() ,
, ![]() ,
, ![]() ,
,
где tp – 100% точка t распределения (p=0,05). Число степеней свободы t распределения равно T-q-1, где q – степень полинома.
Величина tp находится с помощью Мастера – функции в Excel (функция СТЬЮДРАСПОБР).
Таблица 2.15
Расчет среднеквадратической ошибки
| S | Tp | Среднеквадратическая ошибка |
| 0,936056 | 2,014103 | 1,885313 |
| 2,012894 | 1,88418 | |
| 2,011739 | 1,883099 | |
| 2,010634 | 1,882065 | |
| 2,009574 | 1,881073 | |
| 2,00856 | 1,880124 |
Таблица 2.16
Расчет прогноза
| Время | Нижняя граница доверительного интервала для прогноза | Прогноз | Верхняя граница доверительного интервала для прогноза |
| 49 | 36 | 38 | 40 |
| 50 | 37 | 39 | 41 |
| 51 | 39 | 41 | 43 |
| 52 | 40 | 42 | 44 |
| 53 | 42 | 44 | 46 |
| 54 | 44 | 46 | 48 |
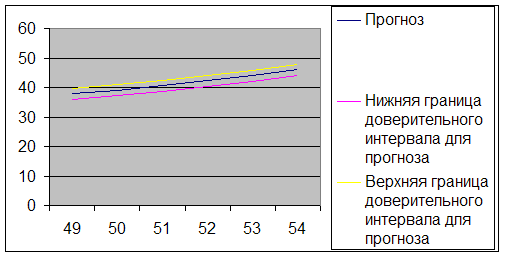
рис. 2.15 - график прогнозов и их доверительных интервалов
По данным прогноза мы видим, что объёмы продаж будут увеличиваться с каждым месяцем. Среднеквадратическая ошибка составляет 2 телеги в месяц.
0 комментариев