Неумение применять теоретическую математику на практике
Определение не должно бать отицающим, Определение должно указывать признаки принадлежащие понятию, а не признаки которые оно не должно иметь
Т.к они подобны
Ердниев П.А., Ердниев Б.П. «Аналогия в задачах» 1989
Пункт
Получают цепочку следствий
Дробные числа появляются как результат измерения величин
Различные приемы введения отрицательных чисел. В учебной литературе можно отметить 3 способа введения отрицательных чисел
Из каких конкретных задач должен возникать вопрос о введении действительного числа и др
Навигация
Т.к они подобны
Теория и методика обучения математике
77352
знака
1
таблица
7
изображений
4 т.к они подобны. В: 1=2, 3=4
4 Силлогизм БП
МП АЕ
ЕД; СЕЕВ; АСВД
В 
АСЕВЕД
Задание: Доказать любую теорему из учебника в форме выделения силлогизмов.
Полная и неполная дедукция.
В том случае когда дедукцией вывод делается после рассматривания не всех частных случаев индукция называется неполной.
Примеры неполной индукции: рассмотрим умножение 2-х чисел
26*24=624
47*43=2021
62*68=4216
сумма единиц-10
первые цифры – одинаковые.
Рассмотрев произведение этих чисел делают вывод. Для любых чисел 
и 
, где сумма
b+c=10, тогда произведение может быть найдено по следующему правилу:
*=a(a+1)*100+bc
этот вывод сделан на основе неполной индукции от частного к общему и нуждается в доказательстве, т.к может оказаться ложным.
Примеры на сокращение дробей:
Из рассматриваемых примеров можно сделать вывод, что в числитель и знаменатель можно вычеркнуть b, а иногда нельзя .
Из приведенных примеров видно что неполная индукция вероятностно умозаключению. Она не может использоваться для доказательства утверждения, но она поможет выделить гипотезы на основании подмеченных закономерностях.
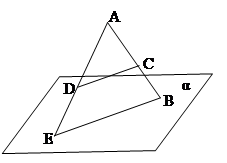
Н-р: Найти ГМТ на плоскости равноудаленных концов отрезка АВ.
Полная индукция противоположность неполной индукции, служит методом строгого логического доказательства.
Может быть использована при доказательстве утверждений относящиеся как к конечному так и бесконечному множеству объекта.
П-р: Значение выражения 
является целым числом при любом х равных 0, -5, 1.
В случае доказательства некоторым утверждениям для бесконечного множества объектов методом полной индукции это множество разделяется на конечное число не пересекающихся подмножеств, которые при объединении должны составлять данное множество.
В школьном курсе полная индукция применяется при доказательстве о величине вписанного угла, теорема косинусов.
Литература:
1. Н.Я. Виленкин «Индукция. Комбинаторика» Москва, 1976
2. Головина Л.И. , Яглан И.М. «Индукция в геометрии» 1956г, Москва.
Аналогия.
Аналогия- является видом традуктивного умозаключения. Она также , как и полная индукция относится к вероятностному умозаключению.
Аналогия- это утверждение, при котором значение об одном объекте переносится на другой объект, сходимый с первым, иногда его называют умозаключение по сходству.
Различают умозаключение простую и распространенную аналогию.
В распространенной аналогии от сходства явлений делают вывод о сходстве причины.
Простая аналогия- это аналогия, в которой от сходства двух объектов в одних признаках, отношениях заключают о сходстве их других признаков и отношениях.
Н-р: Предмет А имеет признаки 1, 2, 3. Предмет В 11, 21, 31- признаки.
В: вероятно объект имеет признак 3 сходный с 31.
Н-р: 1) у прямоугольника все углы прямые (А)
все диагонали равны (В)
точкой пересечения делятся пополам (С).
у прямоугольного параллелепипеда все линейные углы трех равных углов прямые (А)
диагонали равны (В1)
В: (вероятно диагонали параллелепипеда точкой пересечения делятся пополам С1)
Можно заметить сходство треугольника и тетраэдра.
Треугольник выпуклая фигура на плоскости образована наименьшим числом пересечения плоскостей.
Тетраэдр выпуклая фигура в пространстве образуется пересечений плоскостей в пространстве.
Вероятно, свойства у них сходны.
Литература:
Похожие работы
... в психологии. Воспитательные аспекты обучения математике раскрываются в соответствии с концепциями развития личности, которые разработаны в психологии и педагогике. Можно говорить о том, что методика обучения математике как научная область должна иметь такую же структуру, как и любая другая наука, т.е. она должна состоять из отдельных научных теорий. Каждая из них имеет один и тот же объект — ...
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... , умения и навыки; - наличие сильных учеников как группы позволяет постоянно продумывать работу с ними, учитывать возможности их развития. 3. Капиносов А.Н. в статье “Уровневая дифференциация при обучении математике в V-IX классах” [14] рассматривает разбиение учащихся на 4 группы. Основой разбиения являются различия учащихся в темпах овладения учебным материалом, а также в способностях ...
... натурального ряда. В качестве графической модели используем числовой луч, на котором дети отмечают точки, соответствующие натуральным числам. Смысл действий сложения и вычитания. В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение связано с операцией объединения, ...
0 комментариев