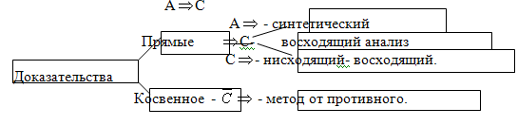
Получают цепочку следствий

2. Получают цепочку следствий

 В1В2…Вх, в которой Вх ложное.

Делают вывод о ложности не . А истина С.

Цели обучения.

I Предметно- ориентированный метод обучения	II личностно-ориентированный метод обучения
Цели: обучающий, развивающий, воспитывающий. Математическое образование. Математика- цель. Ученик- средство. Субъективно объективный. Монолог учителя Формы урока: усвоение = понимание + запоминание Обучение предлагает вооружение алгоритмами. Вооружение учеников готовыми фактами.	образование с помощью математики. Ученик- цель. Математика- средство. Субъективно- объективный диалог Овладение = усваивание + применение на практике Обучение предлагает развитие, отказ от шаблонов стереотипа шаблона. Развитие осуществляется за счет процесса получения фактов.

Лекция 4. Математические задачи

В психолого – методической литературе существуют разные подходы к решению задачи. Большинство авторов считают, что задача – это ситуация требующая действий для достижения определенной цели. Поэтому основными компонентами задачи являются: цель, ситуация, действие.

Цель – это требование, ситуация – условие; действие – решение.

Задачей будем считать математической, если ее решение осуществляется математическими средствами.

2.Математические задачи можно разделять на виды (типы) по разным признакам:

а) по отношению компонентов в математике: чисто математические, (все компоненты математические объекты); прикладные (математическое только решение);

б) по характеру требования Н.М. Фридман

- задачи на вычисление искомого,

- задачи на доказательство и объяснение

- задачи на построение или преобразования.

в) по методу решения подразделяются на арифметические (+,-,/,*), алгебраические (буквенные выражения), геометрическое (построение, преобразование).

г) по числу неизвестных компонентов (Колягин Ю.М.)

- стандартные (все компоненты известны)

- обучающая (неизвестен 1 компонент)

- поисковая (неизвестны 2 компонента)

- проблемная(неизвестны 3 компонента)

Выделяет следующие компоненты: начальное состояние, условие (И), конечное состояние, заключение (Z), решение задачи (N), базис решения обоснование (О).

д) по характеру мыслительной деятельности необходимые для решения: стандартные (репродуктивные), нестандартные (творческие).

е) по дидактическим функциям А.А. Столяр для усвоения понятий задачи, для обучения доказательствам, для формирования математических умений – подготовительные.

Различные признаки типизации задач, связанный с различным методом задач.

Задачи могут выступать как цель: научить решать.

Задачи могут выступать как сод – е обучения: тогда они характеризуются по типу требования.

Задачи в обучении могут выступать как средство обучения; в этом случаи их часто называют упражнениями их назначения давать знания, умения и навыки.

В частности учащегося необходимо обучать методом и приемом решения задач, к ним относятся рассмотренные выше методы как анализ, синтез, дедукция, индукция, аналогия.

Перечислим некоторые приемы решения задач не зависимые от типов задач.

Решение задачи представляет собой такое преобразование условия задачи при котором находится требуемое искомое. Решение математической задачи это значит найти такую последовательность общих положений в математике (определение, аксиомы, формулы, законов и т.д.) применяя которые к условию задачи или к их следствию (промежуточном развитии движения получаем то, что требуется в задачи ее ответ). При решении задачи возникает необходимость четного выделения осиновых этапов решения.

Д. Пойя Ю. М. Калягин выделяют и этапа в процессе решения задачи:

- исследование условия и требования задачи.

- поиск решения задачи (составление плана).

- осуществления планов решения задачи.

- проверка правильности решения задачи, поиск правил других способов решения задачи.

Л. М. Фридман, Е. Н. Турецкий в процессе решения задачи подразделяют на 8 этапов:

- анализ задачи

- схематическая запись задачи,

- поиск правил других способов решения задачи

- осуществления решения задачи

- проверка решения задачи

- исследование задачи

- формирование решения задачи

- анализ решения задачи.

Наиболее важными и трудными являются первые 2 этапа.

Для поиска решения задачи и для анализа и требования используются следующие приемы:

1. правильное чтение задачи (правильное произношение слов, постановка ударения в словах, постановка логических ударений).

2. правильное слушание текста задачи (слушая первый раз надо постараться понять и записать требование задачи, второй раз условие).

3. постановка специальных …. По тексту задачи для выяснения его понимания. Вопросы могут быть следующего характера:

- о чем эта задача?

- о каких объектах идет речь?

- какой процесс описывается в задачи?

- что означают слова, термины, числа?

4. разбиение задачи на смысловые части, выявление структуры задачи, и из формулировки выдвигаются условия и требования, объекты и их характеристики, выясняются отношения, зависимости между ними. Для выполнения условия задачи могут быть поставлены вопросы:

- что дано в задачи?

- что требуется найти?

- как связаны величины задачи?

После такого анализа составляется краткая запись условия задачи.

при необходимости возможна переформировка текста задачи отбросив лишние детали текста.

Приемы поиска планы решения задачи.

1. Распознавание вида задачи, подведение задачи под известные Def, утверждение, правило, алгоритм. В случаи, если задача стандартная.

2. Рассуждение на основе исходного текста задачи с использованием аналитически синтетического метода.

3. рассуждение по краткой записи.

4. проведение аналогии с ранее решенными задачами и методами решения.

5. разбиение задачи на подзадачи.

6. Введение вспомогательных элементов.

Приемы дополнительной работы над задачами.

Составление и решение обратной задачи.

Решение задачи другим способом.

Исследование решения.

Проверка, практическая значимость задачи.

обобщение задачи и способы решения.

Задача: Два велосипедиста выехали навстречу друг другу из пункта А и В, расстояние между которыми = 11 км, ? = 24 км/ч

? = 20 км/ч.

одновременно с первым велосипедистом из А выбежал пес, добежав до 1- го велосипедиста, он повернул назад так он и бегал от одного к другому до их встречи.

Какое расстояние пробежал пес, если его ?= 28 км/ч.

Пери способа: арифметический, арифметически – алгебраический, алгебраический.

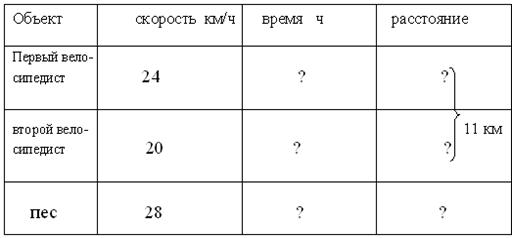
Решение:

S=v/t

t=S/v

v1+2=v1+v2

v1+2=44 км/ч

t=11/44=1/4 ч

S=28:1/4=7 км

При решение задач на вычисление аналитическим способом аналитико – синтетический метод применяется на тех – же решениях. Единственное различие состоит в том , что на этапе поиска решения применяется анализ в нисходящей форме.

Методика обучения решения технических задач.

Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д)

Текстовая- текст

Задача сюжетная- сюжет (реальные объекты, события, явления)

Арифметическая- математические выкладки (коллективные отношения

между значениями нескольких величин, связанные с вычислениями).

Термин текстовая задача -наиболее распространен. Текстовая задача представляет собой словесную модель ситуации, явления, события, процессы.

Задача:

Числовые значения величин (данные, известные- их должно быть не меньше двух).

некоторая система функциональных зависимостей в неявной форме.

требование или вопрос, на который надо найти ответ.

В задачи есть условие. Числовые значения величин и существующие между ними зависимости, т.е качественные и количественные характеристики объектов задачи и отношений между ними.

Величину, значение которой надо найти, называют искомой величиной, а числовое значение искомых величин, а числовое значение искомых величин- искомыми или неизвестными.

Задача: На первом складе было 135 м3 дров, на втором складе 114 м3. Ежедневно с первого склада вывозят по 7,5 м3, со второго 6,5 м3. Через солько дней на складах дров останется поровну?

Условие задачи :

1) Первый склад-135 м3

Второй склад- 114 м3.

Ежедневно с первого склада- по 7,5 м3.

со второго 6,5 м3.

Требование:

Через сколько дней на складах дров останется поровну?

Решение задачи:

135-7,5х=114-6,5х.

135-114=7,5х-6,5х

21=х

х=21

Ответ: через 21 день.

Задача: Даны три числа, сумма которых равна 100. Сумма двух из них равна 80, а первое число на 20 больше второго. Найти эти числа.

Условие задачи :

три числа: x, y, z.

сумма чисел равна 100

сумма двух из них равна 80 (1 и2, 1 и 3, 2 и 3)

первое число на 20 больше второго

Требование: 1. Найти эти числа

Решение задачи:

 

 

 

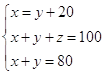
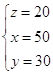
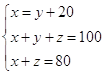
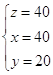
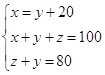
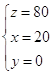
Ответ:

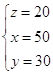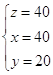1)  2)  3) 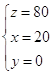- неопределенная задача.

Лекция 5. Алгоритмы и правила

При решении стандартных задач выполняется алгоритмическая деятельность, т.к ход, последовательность и действия учащимся известны, под алгоритмом под алгоритмом понимает предписание, определяющее последовательность действий, операции, преобразовании с данными заданиями и для того чтобы решить задачу определенного типа алгоритм- неопределенное понятие, поэтому его распознавание проводится с использованием характеризующих свойств: массовость, элементарность и дискретность, шагов детерменированность, результативность.

Свойство массовости означает, что алгоритм применим для всех задач данного типа.

Элементарность проявляется в возможности разделения алгоритма на отдельные законченные операции, шаги, каждый из которых ученик может выполнить.

Детерменированность алгоритма понимается как однозначность, определенность каждого его шага.

Результативность показывает, что выполнение предписаний обязательно приводит к требуемому результату.

В школьном курсе математики вместо слова «алгоритм» часто используют термин «правило»

Правило- такое предписание, которое отличается от алгоритма, с нарушением некоторых свойств.

Логико-математический анализ алгоритмов и правил составляют из следующих действий.

а) проверка характеризующих свойств.

б) выделение последовательности операции.

в) установление связи с другими знаниями.

г) установление математических оснований, которые обычно являются общими математическими суждениями.

«Чтобы сложить две дроби с разными знаменателями надо привести их к общему знаменателю и сложить полученные дроби с одинаковыми знаменателями.»

Все свойства алгоритма выполняются, т.к правило применимо для любых двух обыкновенных дробей с разными знаменателями (массовость). В нем четко выделены 2 операции (дискретность) каждая из которой вполне определена (дискретность) и последовательное их выполнение приводит к результату в виде дроби (результативность) с помощью этого правила можно складывать дроби большего количества. Убрав в формулировке слово две. Учителю необходимо пересмотреть правило, указать порядок выполнения действия.

«Чтобы сложить две дроби с разными знаменателями надо:

1) привести их к общему знаменателю

2) сложить полученные дроби с одинаковыми знаменателями.»

Способы задания и виды алгоритмов.

Основными способами задания алгоритмов является словесное предписание в виде свободного текста, памятки, инсрукции, перечня шагов и т.п.

Образец выполнения

Алгоритмичная запись

Блок схемы

Запись на одном из математических языков программирования.

Основные виды алгоритмов: 1. линейные и разветвленные.

2.циклические и нециклические.

Рассмотренный пример «Сложение дробей с разными знаменателями» является линейным нециклическим алгоритмом, заданным способом предписания.

П-р: «Алгоритм Евклида» нахождение НОД двух чисел.

1) Разделить х на у перейти к указанию 2

2) если остаток =0  перейти к указанию 4, иначе к указанию 3.

3) присвоить х значение у, в значение остатка. Перейти к указанию 1.

4) НОД (х,у)= . перейти к указанию 5.

5) процесс окончен.

Это разветвленный циклический алгоритм, заданный способом алгоритм записи «Алгоритм решения линейных уравнений».

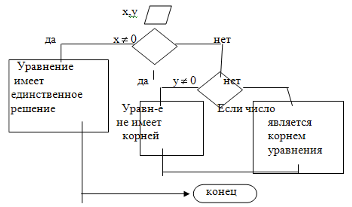
Это разветвленный не циклический алгоритм в виде блок-схемы. В школьном курсе математики алгоритмы и правила чаще записываются в виде и образца выполнения

Развитие понятия числа в курсе математики в неполной средней школе.

Различные подходы изучения чисел в курсе математики в неполной средней школе.

Методические основы ведения новых чисел.

Понятие числа относится к основным понятиям математики. На вопрос «что такое число? »нельзя дать ответ, опираясь на ранее введение понятия.

Современная математика имеет дело с различными по природе числами: натуральные N, с целыми Z, рациональные  Q , действительные числа R, иррациональные J, комплексные С, гиперкомплексные К.

Понятие числа возникло на заре человеческой цивилизации в результате деятельности человека. Постепенно происходило расширение понятия числа.

Nc Z c Q C R c C c r, каждое из этих множеств является расширением предыдущего, при этом имеется в виду, что множество У является расширением множества Х, если выполняются следующее условие:

Множество Х есть собственное подмножество множества У.

Все отношения и операции для элементов множества Х определены и в множестве У, при этом их смысл совпадает с тем, который они имели в Х до расширения.

В множестве У выполнена операция, которая в Х была не выполнима, или не всегда выполнима.

Расширение У является минимальным из всех возможных удовлетворяющим первым трем требованиям.

Первое расширение понятия числа происходит в 5-6 классах, к концу 6-го класса формулируется понятие рационального числа, дальнейшее расширение в 7-9 и далее в 10-11 классах, причем основные положения и представление о числе у учащихся сложились в 5-6 классах.

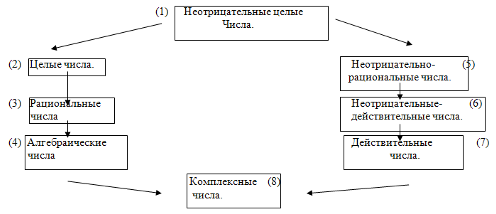
С точки зрения чистой алгебры естественный ряд обобщений идет по пути:

(1)(2)  (3)  (4) и на алгебраических числах заканчивается.

В школе рассмотрение понятия числа идет по пути (1)(5)  (3) (7)(8)

При разработке программы для школы были предложения идти по пути (1)(2)  (3), после того как ученики изучили целые числа должны перейти к понятию неотрицательного числа.

В начале 5-го класса ученики еще не готовы к введению понятия отрицательного числа, они не поймут почему из меньшего числа вычесть больше, а понятие дроби более естественно, оно связано с повседневной жизнью, поэтому выбором путь рассмотрения числа (1)(5)  (3) (7)(8) от (7)(8) оставили на факультативные занятия.

А.А. Столяр предлагает показать учащимся, что расширение понятия числа происходит из потребности практики и в связи с этим предлагает следующую схему:

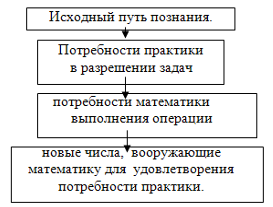
Введение дробных чисел возможно начиная с обыкновенных и десятичных дробей, необходимо исходит из начального освоения. Для первоначального усвоения обыкновенной дроби легче исходя из возраста их жизни, а затем десятичные.

Введение нового числа обычно опирается на жизненный опыт учащихся, необходима мотивировка, так введение дробных чисел связывает с измерением, делением на части, мотивировка может быть алгебраической, практической (вводятся индуктивным методом).

Методика введения новых чисел в школе.

Какие дроби изучали раньше обыкновенные или десятичные?

В большинстве случаев в школе принято изучать обыкновенные дроби, однако есть случаи когда первыми изучают десятичные дроби:

1) десятичные дроби имеют большую практическую ценность.

2) производить действия над десятичными дробями легче

3) теорию о десятичных дробях можно построить, используя понятие обыкновенной дроби, расширяя десятичную нумерацию меньшую единицы.

Доводы против-й стороны:

не следует отступать от исторического развития числа.

Не следует нарушать логику, обыкновенная дробь родовое понятие, а десятичная дробь- видовое, трудно обосновать действия над десятичными дробями без обыкновенной дроби.

Учащиеся не оценят легкость действий над десятичными дробями не познавая трудности при действии над обыкновенными.

Теоретическое значение обыкновенных дробей, выше вся алгебра построена на обыкновенных дробях.

Нумерация дробных чисел.

В нумерации натуральных и дробных чисел есть различия:

1. Натуральное число имеет единственное название и единственное обозначение.

Дробное число имеет бесконечное множество названий и обозначений.

Обыкновенные дроби в отличии от десятичных читается неоднозначно.

При первоначальном введении новых понятий, надо начинать с небольшого 2-3х минутного исторического экскурса.

Источники получения дробных чисел.