Неумение применять теоретическую математику на практике
Определение не должно бать отицающим, Определение должно указывать признаки принадлежащие понятию, а не признаки которые оно не должно иметь
Т.к они подобны
Ердниев П.А., Ердниев Б.П. «Аналогия в задачах» 1989
Пункт
Получают цепочку следствий
Дробные числа появляются как результат измерения величин
Различные приемы введения отрицательных чисел. В учебной литературе можно отметить 3 способа введения отрицательных чисел
Из каких конкретных задач должен возникать вопрос о введении действительного числа и др
Навигация
Дробные числа появляются как результат измерения величин
Теория и методика обучения математике
77352
знака
1
таблица
7
изображений
1. Дробные числа появляются как результат измерения величин.
2. Разделение предметов на доли.
Дробные числа появляются в результате деления одного числа на другое.
Первоначальное ознакомление учащихся с дробью начинается в начальных классах, в 3 классе они знакомятся с долями, методикой ознакомления с простейшими дробями опора на конкретные образы долей величины, на практическое получение той или иной доли, а затем и дроби путем деления предметов, геометрических фигур на нужное число равных частей.
Нельзя допускать формального введения этих понятий.
В начальных классах для введения дроби учащиеся должны:
1) уметь называть и показывать доли со знаменателями не превышающие числа 10. Знать обиходное название этих дробей 
(половина, три, четверть).
2) уметь читать и записывать обыкновенные дроби со знаменателями не превышающие числа 10, показывать соответствующую дроби отрезка.
3) уметь сравнивать с опорой на рисунке указанные выше дроби, без опоры на рисунок уметь сравнивать дроби у которых числитель дроби =1.
4) уметь решать задачи на нахождение доли числа и числа по его долям, а также на нахождение дроби числа.
Каждый раз при решении таких задач используются рисунки, схемы, простые чертежи.
Изучение обыкновенных дробей начинается в 5 классе. В первом издании учебника математики 5- го класса уделялось мало времени на повторение материала 4- го класса.
Во втором издании этого учебника время на повторение увеличено, более обосновано излагается введение дробного числа.
Понятие дроби вводится в объеме достаточным для введения десятичных дробей. Здесь изучаются сведения о дробных числах, необходимых для систематического изучения дробей. Основное внимание уделяется сравнению дробей с одинаковыми знаменателями, а затем к выделению целой части числа. Необходимо чтоб учащиеся поняли, что дроби 
разные записи равных дробных чисел.
Желательно широко использовать различного рода наглядные пособия (бумажные ленты, метод демонстраций, линейки и др.), а также варьировать условие задачи.
Н-р: 1) как записать в виде дроби 3:4=3/4
2) на сколько нужно разделить 3, чтобы получить дробь ¾ (на 4).
При изучении дробных чисел учащиеся должны понять общий вид дробных чисел. Особое место занимает так называемое смешанные числа. Учащиеся должны понимать, что 2+
=2
Смешанное число термин школьный А.А. Колмогоров считает его неудачным и предлагает заменять термином смешанная дробь.
Рассмотрения действия над дробями при малейшем затруднении учащихся необходимо использовать наглядность. Это изображение дроби как части отрезка, прямоугольника, круга. Практика опытных учителей показывает, что следует четче различать отдельные случаи сложения и вычитания обыкновенных дробей с разными знаменателями.
Изучение этого материала лучше проходить в такой последовательности:
1) Сложение дробей , если знаменатель одной из дробей равен остальным.
2) Сложение дробей, если знаменатель одной прост, взаимно простые числа.
3) Приведение дробей к наименьшему общему знаменателю и сложение дробей
4) Примечание законов арифметических действий сложению дробей, содержащих целые и дробные части.
5) Вычитание положительных дробей.
6) Замена единицы дробью при вычитании.
7) Вычитание чисел содержащих целую и дробную часть.
8) Сложение и вычитание рациональных чисел.
Лекция 6. Методика введения понятия отрицательного числа
1. Вопросы, связанные с отрицательными числами являются одним из трудных вопросов для освоения учащимися.
История развития математики показывает, что отрицательные числа значительно труднее дались человеку, это связано с тем, отрицательные числа менее связаны с практической жизнью.
Отрицательные числа возникли в связи с необходимостью выполнения с известными числами. Математики древней Греции не признали отрицательных чисел, они не могли дать им конкретного толкования. Лишь работу Диофанта (3 в. н.э) встречаются преобразования, которые приводят к необходимости выполнения операций над отрицательными числами.
Отрицательные числа появляются лишь в зачаточной форме. Довольно широкое распределение они получили в работах индийских ученых. Положительные числа они называли настоящими, а отрицательные- не настоящими- ложными. Отрицательные числа рассматривали, как долг, а положительные числа как наличные деньги.
Первые правила сложения и вычитания принадлежат индийским ученым. И связаны с трактовкой этих чисел как имущество и долг.
Ученые долго не могли объяснить, дать трактовку произведения двух отрицательных чисел. Почему произведение 2-х долгов есть имущество. Такие ученые как Эйлер, Коми давали свое объяснение правилу произведения чисел, но они приводили к ошибочным результатам.
Немецкий ученый М. Штифель впервые в 1544 г. дал определение отрицательных чисел, как чисел меньших нуля.
Впервые математическую интерпретацию дал Рене Декарт в 1737 г. в книги «Аналитическая геометрия». Отрицательные числа он рассматривал как самостоятельное, расположенное на оси ОХ влево от начало координат. Однако он эти числа назвал ложными. Всеобщее признание отрицательные числа получили в первой половине 21 века, так отрицательные числа вошли в историю математики.
Похожие работы
... в психологии. Воспитательные аспекты обучения математике раскрываются в соответствии с концепциями развития личности, которые разработаны в психологии и педагогике. Можно говорить о том, что методика обучения математике как научная область должна иметь такую же структуру, как и любая другая наука, т.е. она должна состоять из отдельных научных теорий. Каждая из них имеет один и тот же объект — ...
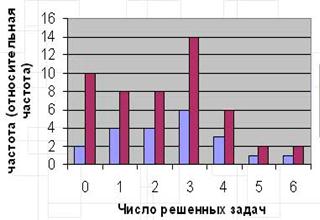
... выборок. 5. Исследовательские проекты и их защита. 3 2 1 2 2 2 1 1 1 3 2 1 2 2 Всего 10 5 10 Итого 60 34 Глава 2 Методика обучения школьников основам комбинаторики, теории вероятностей и математической статистики в рамках профильной школы 2.1. Организация при формировании пространственного образа, c использованием ...
... , умения и навыки; - наличие сильных учеников как группы позволяет постоянно продумывать работу с ними, учитывать возможности их развития. 3. Капиносов А.Н. в статье “Уровневая дифференциация при обучении математике в V-IX классах” [14] рассматривает разбиение учащихся на 4 группы. Основой разбиения являются различия учащихся в темпах овладения учебным материалом, а также в способностях ...
... натурального ряда. В качестве графической модели используем числовой луч, на котором дети отмечают точки, соответствующие натуральным числам. Смысл действий сложения и вычитания. В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение связано с операцией объединения, ...
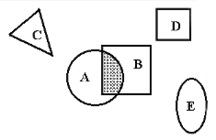
0 комментариев