Каждый этап решения задачи сопровождать краткими, но исчерпывающими пояснениями
Основная задача кинематики
Динамика поступательного и вращательного движения
Некоторые силы в механике
Потенциальная энергия
Элементы специальной теории относительности
Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct
Маховик радиусом R=0,2 м и массой m=10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения
Молекуляро - кинетическая теория идеальных газов
Внутренняя энергия
Распределение Больцмана
Основы термодинамики
Применение первого начала термодинамики к изопроцессам
Цикл Карно и теорема Карно
Фазовое пространство. Микро- и макро- состояния системы
Двухатомному газу сообщено 500 кал тепла. При этом газ расширяется при постоянном давлении. Найти работу расширения газа
Углекислый газ и азот находятся при одинаковых температуре и давлении. Найти для этих газов отношение коэффициентов внутреннего трения
Навигация
Цикл Карно и теорема Карно
Механика, молекулярная физика и термодинамика
121629
знаков
26
таблиц
25
изображений
2.8. Цикл Карно и теорема Карно.
В 1824 г. С. Карно предложил и исследовал идеальный тепловой цикл, названный в последствии циклом Карно. Этот цикл состоит из двух изотерм и двух адиабат (рис.21). Карно также сформулировал две теоремы, определяющие максимальное значение К.П.Д. теплового двигателя.
«Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т1 и Т2 нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего вещества».
«Коэффициент полезного действия всякой тепловой машины не может превосходить коэффициента полезного действия идеальной машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника».
|
| 1®2, 3®4, – изотермические расширение и сжатие, 2®3, 4-1– адиабатические расширение и сжатие. В процессе 1®2 Q1 = В процессе 3®4 U = const, поэтому
|
Рис. 21
, поэтому 
.
.Используя соотношения (48) можно показать, что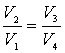 
. Тогда
.
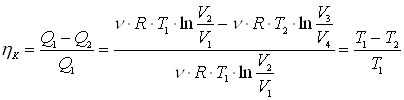2.9. Термодинамическое неравенство Клаузиуса. Энтропия
Рассматривая процессы превращения тепла в работу, Р. Клаузиус сформулировал термодинамическое неравенство, носящее его имя.
«Приведенное количество тепла, полученное системой в ходе произвольного кругового процесса, не может быть больше нуля»
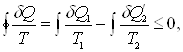
где dQ – количество тепла, полученного системой при температуре Т, dQ1 - количество тепла, получаемое системой от участков окружающей среды с температурой Т1, dQ¢2 – количество тепла, отдаваемое системой участкам окружающей среды при температуре Т2. Неравенство Клаузиуса позволяет установить верхний предел термического К.П.Д. при переменных температурах нагревателя и холодильника.
,
где Т1 макс – максимальная температура участка среды, от которого система получает тепло; Т2 мин – минимальная температура участка среды, которому система отдает тепло.
Из выражения для обратимого цикла Карно следует, что 
или 
, т.е. для обратимого цикла неравенство Клаузиуса переходит в равенство. Это означает, что приведенное количество тепла, полученного системой в ходе обратимого процесса, не зависит от вида процесса, а определяется только начальным и конечным состояниями системы. Поэтому приведенное количество тепла, полученное системой в ходе обратимого процесса, служит мерой изменения функции состояния системы, называемой энтропией.
Энтропия системы – функция ее состояния, определенная с точностью до произвольной постоянной. Приращение энтропии равно приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из начального состояния в конечное по любому обратимому процессу.
, 
.
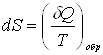Важной особенностью энтропии является ее возрастание в изолированных системах (закон возрастания энтропии).
«Энтропия теплоизолированной (адиабатической) системы не может убывать; она возрастает, если в системе идет необратимый процесс, и остается постоянной при обратимом процессе в системе».
Необратимые процессы в системе приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума и в дальнейшем никакие макроскопические процессы в системе невозможны.
Изменение энтропии при наличии теплообмена с окружающей средой, может быть каким угодно, как больше нуля, так и меньше нуля.
Получим выражение для приращения энтропии идеального газа, при переходе из состояния с параметрами T1, V1, в состояние с параметрами T2, V2 .
.
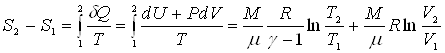Из выражения для приращения энтропии газа следует, что энтропия является функцией двух параметров - температуры и объема S=S(T,V).
Введение энтропии позволяет объединить первое и второе начала термодинамики в виде термодинамического неравенства
,
где знак = относится к обратимым процессам, знак > - к необратимым.
Энтропия, как и внутренняя энергия, связана с микроскопическим строением системы и статистическим характером теплового движения частиц системы.
Похожие работы
... значениями этих параметров, чтобы определить предельные значения и шаг расчёта рассчитываемых параметров. Заключение Хочется выразить уверенность, что в следующих версиях курса "Открытая физика" количество компьютерных моделей будет расти, их функциональные возможности станут разнообразнее, а пределы изменения числовых значений параметров, описывающих эксперименты, будут расширены. Надеемся, что ...
... это количество вещества, взятая в количестве 1 моля. g - количество вещества или число молей. [g]= моль [m]= кг/моль Билет № 7 1. Важным понятием в молекулярной физике и термодинамике является понятие термодинамической системы, к рассмотрению которого мы и переходим. 1.Термодинамической системой (или просто системой) называют совокупность большого числа молекул, атомов или ионов ...
... что разрешало противоречие между результатами Гей-Люссака и Дальтона. Успехи учения об атомно-молекулярном строении вещества, в особенности, газов, безусловно, оказало влияние на становление термодинамики и молекулярной физики и способствовало развитию механической теории теплоты. Во второй половине 18 века господствовала теория теплорода, но уже в начале 19 века она стала уступать свои позиции ...
... : Будем считать величину , измеряемую в энергетических единицах, прямо пропорциональной температуре , выражаемой в градусах: , где - коэффициент пропорциональности. Коэффициент , в честь австрийского физика Л.Больцмана называется постоянной Больцмана. Следовательно, . Температура, определяемая этой формулой, не может быть отрицательной. Следовательно, наименьшим возможным значением температуры ...
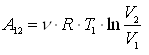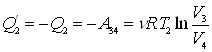0 комментариев