Молекуляро - кинетическая теория идеальных газов

1. Молекуляро - кинетическая теория идеальных газов

1.1.  Уравнение состояния

В состоянии термодинамического равновесия объем V, давление Р и температура Т находятся в функциональной зависимости, которую можно выразить уравнением

F (P,V,T) = 0.

Это соотношение называется уравнением состояния тела (системы). Вид функции F(P,V,T) различен для разных тел и точно установлен только в одном случае, а именно, для идеального газа. Идеальным называется газ, в котором

,

где t^¢- среднее время столкновения частиц, t - среднее время свободного пробега частиц. При этом средняя длина свободного пробега частиц должна быть много меньше размеров сосуда, в котором заключен газ. Данные условия выполняются достаточно хорошо для газов, молекулы которых имеют простое строение, даже при давлениях близких к атмосферному.

Уравнение состояния идеального газа можно получить, рассмотрев давление, создаваемое газом на стенку сосуда. Оно возникает в результате передачи импульса участку стенки при столкновениях с ним молекул газа. Учитывая, что в равновесном состоянии соударения молекул в среднем носят упругий характер, давление идеального газа оказывается пропорциональным средней энергии поступательного движения частиц, заключенных в единице объема

,

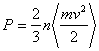где n – плотность (концентрация) частиц, n = N/V, N – число частиц.

Используя связь кинетической энергии молекул и температуры, получаем

P = nkT.

Существует несколько форм записи этого уравнения

PV = NkT

PV = N_AkT = nRT.

В ней n =- число молей газа, R = N_Ak = 8.31 Дж/моль×К – универсальная газовая постоянная. Используя выражение для количества вещества через массу и молярную массу газа можно получить известное уравнение Клапейрона – Менделеева

PV =RT.

Из последнего уравнения состояния можно получить известный закон Дальтона и уравнения изопроцессов:

а) давление механической смеси газов равно сумме парциальных давлений газов, входящих в смесь

PV = ()RT

б) изотермический – Т=const, PV = const, P₁V₁ = P₂V₂;

изобарический - P = const,  ;

изохорический - V = const, .

 1.3 Уравнение состояния Ван-дер-Ваальса

При увеличении плотности (давления) поведение газа все сильнее отличается от поведения идеального газа. Это объясняется тем, что при малых средних расстояниях между молекулами, все большее значение приобретают силы межмолекулярного взаимодействия. На малых расстояниях эти силы являются силами отталкивания, а на больших - силами притяжения. Влияние этих сил на вид уравнения состояния можно приближенно учесть следующим образом. Для реальных газов давление должно резко возрастать при конечном объеме, равном по порядку величины объему всех частиц газа. Обозначим этот конечный объем для одного моля через – b, тогда давление газа может быть записано в виде

Действие сил притяжения между молекулами проявляется в уменьшении давления газа по сравнению с приведенной величиной. Уменьшение давления связано с тем, что на молекулу, находящуюся у стенки сосуда, действует сила направленная внутрь сосуда. Она обусловлена притяжением со стороны молекул газа, находящихся в его объеме. В первом приближении ее величина пропорциональна концентрации молекул n =, а, учитывая, что давление само пропорционально концентрации, поправка на уменьшение давления будет пропорциональна n²=. Учитывая это можно прийти к соотношению

P = ,

которое в форме

 называется уравнением Ван-дер-Ваальса (для одного моля газа). Поправки a и b- постоянные Ван-дер-Ваальса, учитывающие, соответственно, действие сил притяжения и отталкивания между молекулами газа.

Похожие работы

КОМПЬЮТЕРНЫЕ МОДЕЛИ в ФИЗИКЕ

Скачать

40136

0

23

... значениями этих параметров, чтобы определить предельные значения и шаг расчёта рассчитываемых параметров. Заключение Хочется выразить уверенность, что в следующих версиях курса "Открытая физика" количество компьютерных моделей будет расти, их функциональные возможности станут разнообразнее, а пределы изменения числовых значений параметров, описывающих эксперименты, будут расширены. Надеемся, что ...

Физика (лучшее)

Скачать

147222

0

1

... это количество вещества, взятая в количестве 1 моля.   g - количество вещества или число молей. [g]= моль [m]= кг/моль Билет № 7   1. Важным понятием в молекулярной физике и термодинамике является понятие термодинамической системы, к рассмотрению которого мы и пе­реходим. 1.Термодинамической системой (или просто системой) называют совокупность большого числа молекул, атомов или ионов ...

История физики: термодинамика и молекулярная физика

Скачать

24048

0

0

... что разрешало противоречие между результатами Гей-Люссака и Дальтона. Успехи учения об атомно-молекулярном строении вещества, в особенности, газов, безусловно, оказало влияние на становление термодинамики и молекулярной физики и способствовало развитию механической теории теплоты. Во второй половине 18 века господствовала теория теплорода, но уже в начале 19 века она стала уступать свои позиции ...

Молекулярная физика

Скачать

31367

0

1

... : Будем считать величину , измеряемую в энергетических единицах, прямо пропорциональной температуре , выражаемой в градусах: , где - коэффициент пропорциональности. Коэффициент , в честь австрийского физика Л.Больцмана называется постоянной Больцмана. Следовательно, . Температура, определяемая этой формулой, не может быть отрицательной. Следовательно, наименьшим возможным значением температуры ...