Навигация
Фазовое пространство. Микро- и макро- состояния системы
2.10. Фазовое пространство. Микро- и макро- состояния системы.
Статистический анализ поведения системы свидетельствует о том, что вероятность состояния и энтропия ведут себя схожим образом, а, именно, при переходе системы к равновесному состоянию и энтропия, и вероятность возрастают. Для установления точного соотношения между ними необходимо ввести статистическое описание системы с микроскопической и макроскопической точек зрения. Это возможно путем введения фазового пространства, в котором движутся частицы системы. Фазовое пространство – шестимерное пространство, по осям которого откладываются значения координат и проекций импульсов частиц (x, y, z, px, py, pz). Учитывая, что динамические переменные изменяются непрерывно, вести описание состояний с указанием точных значений координат и импульсов для каждой частицы невозможно. Поэтому все фазовое пространство разбивается на фазовые ячейки, объемом DV=DxDyDzDpxDpyDpz. Теперь состояние каждой частицы может быть определено указанием того, в какой фазовой ячейке она находится.
Состояние системы, заданное указанием того, какие частицы находятся в каждой фазовой ячейке, называется микросостоянием системы.
С макроскопической точки зрения состояние системы зависит от того, сколько частиц имеют то или иное значение энергии или сколько частиц находится вблизи данной точки системы, но не какие именно это частицы. Поэтому
Состояние системы, заданное указанием того, сколько частиц находится в каждой фазовой ячейке, называется макросостоянием системы.
При подобном описании состояния системы, перемещения частиц в пределах фазовой ячейки не изменяют ни микро- ни макро- состояние. Переходы частиц из одной ячейки в другую при неизменном их числе в каждой фазовой ячейке изменяют микросостояние, но оставляют прежнее макросостояние. Таким образом, одно и тоже макроскопическое состояние может быть реализовано при самых различных микросостояниях. Это приводит к тому, что вероятность возникновения того или иного макросостояния системы зависит от числа микросостояний, реализующих данное макросостояние.
2.11. Статистический вес (термодинамическая вероятность) макросостояния и его связь с энтропией.
«Количество различных микросостояний, реализующих данное макросостояние системы, называется статистическим весом или термодинамической вероятностью макросостояния».
Все микросостояния системы равновероятны, а вероятность (математическая) макросостояния определяется ее статистическим весом. Анализ значений статистических весов различных макросостояний показывает, что в равновесном состоянии статистический вес максимален. Это означает, что все макроскопические процессы обладают односторонней направленностью. Переход между двумя макроскопическими состояниями возможен только в том случае, если конечное состояние является более вероятным, чем начальное. В этом заключается механизм необратимости тепловых процессов, которая проявляется в стремлении всех макроскопических тел перейти в равновесное состояние. С другой стороны, статистика не исключает самопроизвольных переходов в неравновесные состояния, просто эти переходы маловероятны (статистические флуктуации).
Получим выражение для статистического веса макросостояния. Пусть в системе имеется N частиц, а все фазовое пространство (область возможных значений координат и импульсов) разбито на m ячеек. Рассчитаем статистический вес состояния при котором: в 1ой ячейке находится N1 частиц; во 2ой ячейке – N2 частиц; и т.д.; в mой ячейке - Nm частиц. Для этого достаточно рассчитать число возможных перестановок частиц между ячейкам (они не изменяют числа частиц в ячейках). Это можно сделать, если из общего числа перестановок N частиц N! , исключить перестановки в пределах каждой ячейки Ni! (они ничего не изменяют).
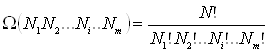 .
.
Если в системе создать искусственно неравновесное состояние, то в подавляющем большинстве случаев система самопроизвольно будет переходить в состояние с большей вероятностью. С другой стороны, согласно термодинамике, все самопроизвольные процессы в замкнутой системе, сопровождаются возрастанием энтропии. Поэтому следует ожидать, что между энтропией системы S в каждом состоянии и вероятностью W того же состояния должна существовать однозначная связь. Эта связь была установлена Больцманом (формула Больцмана)
![]() ,
,
где k – постоянная Больцмана.
Последнее соотношение можно рассматривать как определение энтропии. При таком понимании энтропии закон ее возрастания утрачивает свою абсолютность и становится статистическим законом. Энтропия замкнутой системы может не только возрастать, но и убывать. Это можно трактовать следующим образом: если система находится в неравновесном состоянии, то переход ее в более вероятное состояние будет происходить в подавляющем большинстве случаев, переходы же в менее вероятные состояния (с меньшей энтропией) настолько маловероятные, что практически не имеют никакого значения. Тогда закон возрастания энтропии оправдывается на практике с абсолютной достоверностью.
Примеры решения задач
Задача 1 Смесь азота и гелия при температуре 27 0С находится под давлением р=1,3×102 Па. Масса азота составляет 70 % от общей массы смеси. Найти концентрацию молекул каждого из газов.
| T = 300 К p = 1,3×102 Па M1 = 0,7 M | Решение При данном давлении газ можно считать идеальным. Согласно основному уравнению молекулярно-кинетической теории: р=nkT, откуда n=p/kT. С одной стороны, масса каждого из газов: M1=c1M, (1) |
| n1 - ? n2 - ? |
M2=c2M,
где M - масса смеси;
с1 и с2 – процентное содержание азота и гелия.
С другой стороны, масса каждого из газов:
 (2)
(2)
где V – объем газа;
m - молярная масса газа;
mi/NА – масса молекулы.
Приравнивая правые части уравнений (1) и (2), получим:
c1M=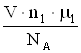 ; c2M=
; c2M=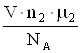 ;
;
откуда n1/n2=![]() =1/3. Так как n1+n2=n,
=1/3. Так как n1+n2=n,
то n1=![]() =0,8×1022 м-3, n2=
=0,8×1022 м-3, n2=![]() =2,4×1022 м-3.
=2,4×1022 м-3.
Ответ: n1=![]() =0,8×1022 м-3, n2=
=0,8×1022 м-3, n2=![]() =2,4×1022 м-3.
=2,4×1022 м-3.
Задача 2 Найти среднюю квадратичную скорость, среднюю кинетическую энергию поступательного движения и среднюю полную кинетическую энергию молекул азота и гелия при температуре 27 0С. Определить полную энергию всех молекул 100 г каждого из газов.
| T = 300 К M1 = 0,1 кг mНе = 4×10-3 кг/моль mN2 = 28×10-3 кг/моль | Решение Средняя кинетическая энергия поступательного движения одной молекулы идеального газа определяется как <Е>= <E>=6,2×10-21 Дж, причем средние энергии поступательного движения одной молекулы азота и гелия одинаковы. Средняя квадратичная скорость молекул газа зависит от массы его молекул: |
| <uкв> - ? E- ? W - ? |
<uкв>=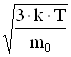 . (1)
. (1)
<uкв>=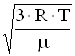 ;
;
<uкв>=13,7×102 м/с – для гелия;
<uкв>=5,17×102 м/с – для азота.
Средняя полная энергия молекулы зависит от числа степеней свободы молекулы:
<E0>=![]() .
.
Полная кинетическая энергия всех молекул, равная для идеального газа его внутренней энергии, может быть найдена как произведение Е0 на число всех молекул:
Е=U=Е0×N; N=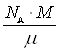 .
.
Гелий – одноатомный газ Þ i=3, тогда <E0>=6,2×10-21 Дж.
Азот – двухатомный газ Þ i=5, тогда <E0>=10,4×10-21 Дж.
Полная энергия всех молекул
Е= .
.
Для гелия W=93,5×103 Дж; для азота W=22,3×103 Дж.
Ответ: для гелия W=93,5×103 Дж; для азота W=22,3×103 Дж
Задача 3 Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении р=105 Па и температуре 17 0С. Как изменятся найденные величины в результате двукратного увеличения объема газа: 1) при постоянном давлении; 2) при постоянной температуре? Эффективный диаметр молекул азота d=3,7×10-8см.
| p = 105 Па T = 300К V2 = 2V1 1) p – const 2) T – const d = 3,7×10-10 м | Решение Средняя длина свободного пробега и коэффициенты переноса могут быть рассчитаны по следующим формулам: где n – концентрация молекул газа; <u> - средняя скорость молекулы; m0 – масса одной молекулы; |
| l - ? D - ? h - ? |
Концентрацию молекул можно определить из уравнения p=nkT:
n=p/kT подставим в уравнение (1):
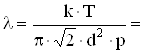 6,5×10-8 м.
6,5×10-8 м.
Средняя скорость <u>=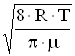 =470 м/с;
=470 м/с;
Тогда D=1×10-5 м2/с.
Для расчета h подставим (1) в (3):
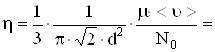 1,2×10-5
1,2×10-5![]() .
.
Как видно из выражения (1), длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объема концентрация уменьшится вдвое. Следовательно, при любом процессе l2/l1=2.
В выражение для коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Тогда:
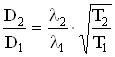
При р=const объем прямо пропорционален температуре: Т2/Т1=V2/V1=2, тогда D2/D1=![]() .
.
При Т=const D2/D1=l2/l1=2.
Вязкость зависит от скорости молекул, следовательно, и от температуры, т.е.
 ,
,
при р=const ![]()
![]() ;
;
при Т=const ![]() .
.
Ответ: l=6,5×10-8 м; D=1×10-5 м2/с; h=1,2×10-5![]() .
.
Задача 4 Пылинки массой 10-18 г. взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура воздуха во всем объеме одинакова: Т=300 К.
| m1 = 10-21 кг T = 300 К
| Решение При равновесном распределении пылинок их концентрация зависит только от координаты z по оси, направленной вертикально. По распределению Больцмана: n=n0×e-u/kT=n0×e-mgz/kT. (1) |
| DZ - ? |
Дифференцируя выражение (1) по z, получим
dn=-n0×![]() ×e-mgz/kT×dz.
×e-mgz/kT×dz.
Так как n0×e-mgz/kT=n, то dn=-![]() ×n×dz. Отсюда dz=
×n×dz. Отсюда dz=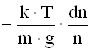 .
.
Знак «-» показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0). Знак «-» опускаем и заменяем dz и dn конечными приращениями Dz и Dn:
 .
.
Dn/n=0,01 по условию задачи. Подставляя значения, получим Dz=4,23 мм.
Ответ: Dz=4,23 мм
Задача 5 Вычислить удельные теплоемкости сv и сp смеси неона и водорода. Массовые доли газов w1=0,8 и w2=0,2. Значения удельных теплоемкостей газов – неон: сv=6,24 ![]() ; cp=1,04
; cp=1,04![]() ; водород: сv=10,4
; водород: сv=10,4![]() ; сp=14,6
; сp=14,6![]() .
.
| w1 = 0,8 w2 = 0,2 cV1 = 6,24 кДж/кг × К cp1 = 1,04 кДж/кг × К cV2 = 10,4 кДж/кг × К cp2 = 14,6 кДж/кг × К | Решение Теплоту, необходимую для нагревания смеси на DТ, выразим двумя соотношениями: где сv – удельная теплоемкость смеси, M1 – масса неона, M2 – масса водорода, и где cv1 и сv2 – удельные теплоемкости неона и водорода соответственно. |
| cp - ? cv- ? | Приравняв правые части выражений (1) и (2) и разделив обе части полученного равенства на DТ, найдем: |
![]() ,
,
откуда 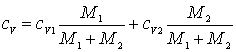 .
.
Отношения 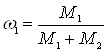 и
и 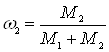 выражают массовые доли неона и водорода соответственно. С учетом этих обозначений последняя формула примет вид:
выражают массовые доли неона и водорода соответственно. С учетом этих обозначений последняя формула примет вид:
![]() ,
,
Подставляя значения, получим сv=2,58×103![]() .
.
Таким же образом получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:
![]()
Подставляя значения, получим ср=3,73103![]() .
.
Ответ: сv=2,58×103![]() ; ср=3,73103
; ср=3,73103![]() .
.
Задача 6 Кислород массой M=2 кг занимает объем v1=1 м3 и находится под давлением p1=2атм= 2,02×105 Па. Газ был нагрет сначала при постоянном давлении до объема V2=3 м3, а затем при постоянном объеме до давления
p2=5атм=5,05×105 Па. Найти изменение внутренней энергии газа DU, совершенную им работу А и теплоту, переданную газу. Построить график процесса.
| M = 2 кг V1 = 1 м3 p1 = 2,02× 105 Па p – const V2 = 3 м3 V – const p2 = 5,05 × 105 Па | Решение Изменение внутренней энергии газа определяется по формуле Из уравнения Менделеева - Клапейрона Подставляя в формулу (2) значения давления и объема, получим значения температуры: Т1=389 К, Т2=1167 К. Из уравнения (1) DU=3,28×106 Дж. Работа рассчитывается по формуле
при p=const А1=0,404×106 Дж; |
| DU - ? A- ? Q - ? |
V=const А2=0.
Полная работа, совершенная газом: А=А1+А2=0,404×106 Дж.
На основании первого начала термодинамики![]()
получаем теплоту, переданную газу: Q=3,68×106 Дж.
![]() График процесса изображен на рисунке: p
График процесса изображен на рисунке: p
![]()
![]() p2 3
p2 3
![]()
![]()
![]()
![]() p1 1 2
p1 1 2
v
![]() v1 v2
v1 v2
Ответ: DU=3,28×106 Дж; А=0,404×106 Дж; Q=3,68×106 Дж.
Задача 7 Идеальная тепловая машина работает по циклу Карно нагретым воздухом, взятом при начальном давлении 7×105 Па и температуре 127 0С. Начальный объем воздуха 2×10-3 м3. После первого изотермического расширения воздух занял объем 5 л, после адиабатического расширения объем стал равен 8 л. Найти координаты пересечения изотерм и адиабат.
| p1 = 7× 105 Па T1 = 400К V1 = 2 × 10-3 м3 T – const V2 = 5 × 10-3 м3 Q – const V3 = 8 × 10-3 м3 |
Решение Уравнение изотермы АВ имеет ви |
| V1-?, р1-?, V2-?, р2-?, V3-?, р3-?, V4-?, р4-?. |
Для точки А 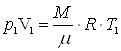 , откуда
, откуда  ,
, ![]() =0,427 молей, тогда уравнение (1) примет вид:
=0,427 молей, тогда уравнение (1) примет вид:
pV = 0,427×8,31×400=1420 Дж.
Для точки В  =284×103 Па.
=284×103 Па.
![]() , откуда
, откуда 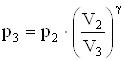 =1,44×105 Па.
=1,44×105 Па.
Уравнение изотермы DС 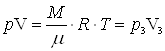 =1,44×1,05×105×8×10-3=1170 Дж. Отсюда Т2=330 К.
=1,44×1,05×105×8×10-3=1170 Дж. Отсюда Т2=330 К.
Так как координаты точек Д и А должны удовлетворять уравнению адиабаты, то
 ,
,
отсюда V4=3,22×10-3 м3 и ![]() 105 = 3,6×105 Па.
105 = 3,6×105 Па.
Таким образом: V1=2×10-3 м3, р1=7×105 Па,
V2=5×10-3 м3, р2=2,8×105 Па,
V3=8×10-3 м3, р3=1,44×105 Па,
V4=3,22×10-3 м3, р4=3,6×105 Па.
Задача 8 Найти изменение энтропии при нагревании воды массой M=100 г от температуры t1=0 0С до температуры t2=100 0С и последующем превращении воды в пар той же температуры.
| M = 0,1 кг t1 = 0 °C t2 = 100°C | Решение Найдем отдельно изменение энтропии DS/ при нагревании воды и изменение энтропии DS// при превращении воды в пар. Полное изменение энтропии выразится суммой DS/ и DS//. Изменение энтропии выражается формулой |
| DS - ? |
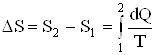 (1)
(1)
При бесконечно малом изменении dT температуры нагреваемого тела затрачивается количество теплоты dQ=McdT, где M – масса тела, с – его удельная теплоемкость. Подставив dQ в формулу (1), получим формулу для вычисления изменения энтропии при нагревании воды:
![]()
![]() ;
;
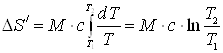 ;
;
DS/=132 Дж/К.
При вычислении по формуле (1) изменения энтропии во время превращения воды в пар той же температуры T = const, и тогда
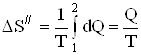 , (2)
, (2)
где Q – количество теплоты, переданное при превращении нагретой воды в пар той же температуры.
Подставив в равенство (2) выражение количества теплоты ![]() , где
, где
l - удельная теплота парообразования, получим:
![]() ;
;
DS//=605 Дж/К.
Полное изменение энтропии при нагревании и последующем превращении ее в пар DS=DS/+DS//=737 Дж/К.
Ответ: DS/=132 Дж/К; DS//=605 Дж/К.
Задачи, рекомендуемые для самостоятельного решения
1. Сосуд емкостью V=10-2 м3 разделен пополам полунепроницаемой перегородкой. В одну половину сосуда введено 2 г водорода и 4 г гелия. Через перегородку может диффундировать только водород. Во время процесса поддерживается температура 100 0С. Считая газы идеальными, определить установившееся давление в обеих частях сосуда.
Ответ: p=9,6×105 Па
2. Полагая температуру воздуха и ускорение свободного падения не зависящими от высоты, определить, на какой высоте h над уровнем моря плотность воздуха меньше своего значения на уровне моря в 2 раза. Температура воздуха t=0 0С.
Ответ: h=5,5 км
3. Температура окиси азота NO Т=300 К. Определить долю молекул, скорость которых находится в интервале от u1=820 м/с до u2=830 м/с.
Ответ: DN/N=0,4 %
4. В баллоне вместимостью 10 дм3 находится гелий массой 2 г. Определить среднюю длину свободного пробега молекул гелия.
Ответ: l=0,21×10-6 м
5. Вычислить удельные теплоемкости неона и водорода при постоянном объеме сv и давлении сp, принимая эти газы за идеальные.
Ответ: сv1=624![]() , cp1=1,04×103
, cp1=1,04×103![]() , cv2=10,4×103
, cv2=10,4×103![]() , cp2=14,6×103
, cp2=14,6×103![]() .
.
Похожие работы
... значениями этих параметров, чтобы определить предельные значения и шаг расчёта рассчитываемых параметров. Заключение Хочется выразить уверенность, что в следующих версиях курса "Открытая физика" количество компьютерных моделей будет расти, их функциональные возможности станут разнообразнее, а пределы изменения числовых значений параметров, описывающих эксперименты, будут расширены. Надеемся, что ...
... это количество вещества, взятая в количестве 1 моля. g - количество вещества или число молей. [g]= моль [m]= кг/моль Билет № 7 1. Важным понятием в молекулярной физике и термодинамике является понятие термодинамической системы, к рассмотрению которого мы и переходим. 1.Термодинамической системой (или просто системой) называют совокупность большого числа молекул, атомов или ионов ...
... что разрешало противоречие между результатами Гей-Люссака и Дальтона. Успехи учения об атомно-молекулярном строении вещества, в особенности, газов, безусловно, оказало влияние на становление термодинамики и молекулярной физики и способствовало развитию механической теории теплоты. Во второй половине 18 века господствовала теория теплорода, но уже в начале 19 века она стала уступать свои позиции ...
... : Будем считать величину , измеряемую в энергетических единицах, прямо пропорциональной температуре , выражаемой в градусах: , где - коэффициент пропорциональности. Коэффициент , в честь австрийского физика Л.Больцмана называется постоянной Больцмана. Следовательно, . Температура, определяемая этой формулой, не может быть отрицательной. Следовательно, наименьшим возможным значением температуры ...
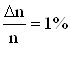
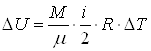 . (1)
. (1)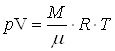 , выразим температуру:
, выразим температуру: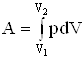

 . (1)
. (1)
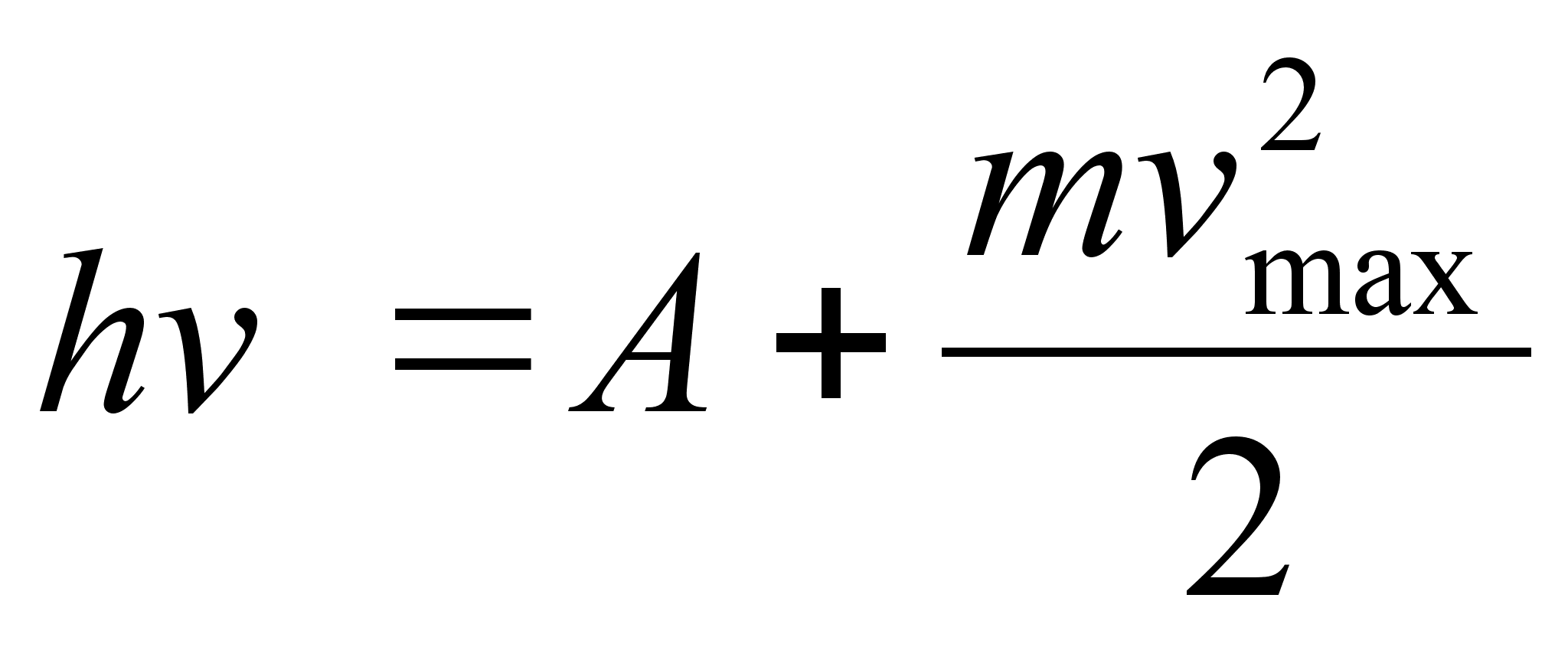


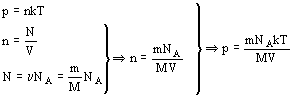
0 комментариев