Каждый этап решения задачи сопровождать краткими, но исчерпывающими пояснениями
Основная задача кинематики
Динамика поступательного и вращательного движения
Некоторые силы в механике
Потенциальная энергия
Элементы специальной теории относительности
Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct
Маховик радиусом R=0,2 м и массой m=10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения
Молекуляро - кинетическая теория идеальных газов
Внутренняя энергия
Распределение Больцмана
Основы термодинамики
Применение первого начала термодинамики к изопроцессам
Цикл Карно и теорема Карно
Фазовое пространство. Микро- и макро- состояния системы
Двухатомному газу сообщено 500 кал тепла. При этом газ расширяется при постоянном давлении. Найти работу расширения газа
Углекислый газ и азот находятся при одинаковых температуре и давлении. Найти для этих газов отношение коэффициентов внутреннего трения
Навигация
Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct
Механика, молекулярная физика и термодинамика
121629
знаков
26
таблиц
25
изображений
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c2 = 2,4 м/с2;
a2 = 6×0,2×5 м/с2 = 6 м/с2.
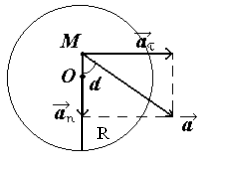
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 
любой точки маховика с радиусом в тот момент, когда маховик совершит первые N=2 оборота.
Дано:
| w0 = 0. N = 2 e = const | Решение Разложив вектор |
| a - ? |
точки М на тангенциальное 
и нормальное 
ускорения, видим, что искомый угол определяется соотношением tga=at/an. Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы:at= eR, an = w2R, где R – радиус маховика, получим
|
|
tga =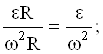 
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
;
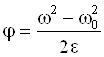Поскольку w0 = 0; j = 2pN, то w2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:
a » 2,3°.
Ответ: a » 2,3°.
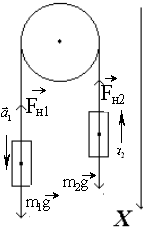
Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 
. Трением в блоке пренебречь.
Дано:
| m1 = 2 кг m2 = 1 кг | Решение Воспользуемся для решения задачи основным законом динамики где |
| a, FН - ? |
– равнодействующая всех сил, действующих на тело. На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем:
(1)
|
|
для второго тела:
.
(2)
Так как сила трения в блоке отсутствует,
.
Ускорения тел а1 и а2 равны по модулю и направлены в противоположные стороны
.
Получаем из (1) и (2) систему уравнений.
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений 
в проекциях на ось Х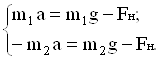 
Решая эту систему относительно а и FН, получаем:
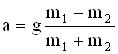= 3,3 м/с2; 
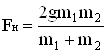= 13 Н.
Ответ: a = 3,3 м/c2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с2.
Дано:
| R = 0,2 м F = 98,1 Н MТР = 4,3 Н×м e = 100 рад / c2 | Решение Воспользуемся основным законом динамики вращательного движения:
|
| m - ? |
или в скалярной форме
, где
- момент сил, приложенных к телу ( MF - момент силы F, Mтр – момент сил трения );
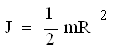- момент инерции диска.
Учитывая, что MF=F×R, получаем: 
.
Отсюда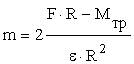 
m = 7,7 кг.
Ответ: m = 7,7 кг.
Задача 5
Вагон массой 20 т, движущийся равнозамедленно, под действием силы трения в 6 кН через некоторое время останавливается. Начальная скорость вагона равна 54 км/ч. Найти работу сил трения и расстояние, которое вагон пройдет до остановки.
Дано:
| m = 20 × 10 3 кг Fтр = 6 × 10 3 Н u = 15 м/c | Решение По закону сохранения механической энергии изменение полной механической энергии будет определятся работой неконсервативных сил, то есть
|
| AТР - ? r - ? | Так как механическая энергия вагона равна его кинетической энергии, в качестве неконсервативной силы выступает сила |
.трения, в конце пути скорость вагона равна нулю, то
.
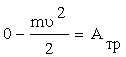Итак: 
По определению для работы, совершаемой постоянной силой трения:
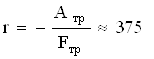м.
Ответ: r = 375 м.
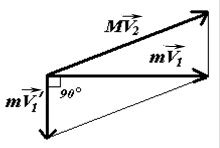
Задача 6 При упругом ударе нейтрона о ядро атома углерода он движется после удара в направлении, перпендикулярном начальному. Считая, что масса М ядра углерода в n=12 раз больше массы m нейтрона, определить, во сколько раз уменьшается энергия нейтрона в результате удара.
Дано:
|
| Решение Ведем обозначения: u1 – скорость нейтрона до удара, u1’ – после удара; u2 – скорость ядра углерода после удара (до удара она равна нулю). По законам сохранения импульса и энергии соответственно имеем: |
| a - ? |
|
|
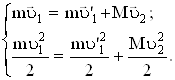
По условию задачи требуется найти отношение
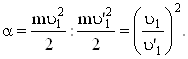
Из треугольника импульсов (смотри рисунок) имеем:
(mu1)2+(mu¢1)2=(Mu2)2.
С учетом записанных выражений, а также соотношения n=M/m, получим:
u12-u¢12=nu22;
u12+u¢12=n2u22.
Разделив почленно последние равенства, получаем:
.
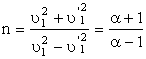Отсюда 
=1,18.
Ответ: a = 1,18.
Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой I=130 кг×м2, вращается по инерции вокруг вертикальной оси, делая n1=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
Дано:
| R = 1м I = 130 кг × м2 n1 = 1c-1 m = 70 кг | Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа – человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме: L1 = L2 , (1) |
| n2 - ? |
где L1 - импульс системы с человеком, стоящим на краю платформы, L2 - импульс системы с человеком, стоящим в центре платформы.
L1 = I1w1 = (I+mR2)×2pn1, (2)
L2 = I2w2 = I×2pn2, (3)
где mR2 - момент инерции человека, I1 = I+mR2 - начальный момент инерции
системы, I2 - конечный момент инерции системы, w1 и w2 - начальная и конечная угловые скорости системы. Решая систему уравнений (1) - (3), получаем:
n2 = n1(I+mR2)/I = 1,5 об/с.
Ответ: n2 = 1,5 с-1.
Задача 8
Определить кинетическую энергию (в электронвольтах) и релятивистский импульс электрона, движущегося со скоростью u = 0,9 c (
-скорость света в вакууме).
Дано:
| u = 0,9 c | Решение Т.к. скорость частицы сопоставима по значению со скоростью света в вакууме, то частицу нельзя считать классической. Для нахождения кинетической энергии воспользуемся формулой: |
| ЕК, р - ? |
.
- масса покоя электрона . 
Так как 
,то 
Можно было найти значение кинетической энергии сразу в электрон вольтах, учитывая, что энергия покоя электрона 
Релятивистский импульс находим по формуле
,
.
Ответ: EK» 0,66 МэВ; р » 5,6 ×10-22 кг×м/c.
Задачи для самостоятельного решения
1. Поезд движется прямолинейно со скоростью u0 = 180 км/ч. Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость поезда изменяется по закону u = u0-at2, где а=1м/с3. Каков тормозной путь поезда? Через какое время после начала торможения он остановится?
Ответ: х»235 м, t»7 с
2. Колесо радиусом R=0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j=A+Bt+Ct3, где А, В, С – постоянные; В=2 рад/с и С=1 рад/с3. Для точек, лежащих на ободе колеса, найти через 2 с после начала движения следующие величины: 1) угловую скорость; 2) линейную скорость; 3) угловое ускорение; 4) тангенциальное ускорение; 5) нормальное ускорение.
Ответ: w=14 рад/с; u=1,4 м/с; e=12 рад/с2; at=1,2 м/с2; an=19,6 м/с2.
3. По наклонной плоскости, образующей угол a с горизонтом, скользит тело. Коэффициент трения тела с плоскостью m. Определить ускорение, с которым движется тело.
Ответ: a = g(sina - m×cosa)
4.Тонкий однородный стержень длиной L=50 см и массой m=400 г вращается с угловым ускорением 
вокруг оси, проходящей перпендикулярно стержню через его середину. Определить момент силы, под действием которой вращается стержень.
Ответ: M=0,025 Н×м
5. Камень брошен под углом 600 к поверхности земли. Кинетическая энергия камня в начальный момент равна 20 Дж. Определить кинетическую и потенциальную энергии камня в наивысшей точке его траектории. Сопротивлением воздуха пренебречь.
Ответ: 5 Дж; 15 Дж.
6. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго 100 г. Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если удар неупругий?
Ответ: H » 2см
7. Тонкий однородный стержень длиной L может вращаться вокруг горизонтальной оси, проходящей через конец стержня перпендикулярно ему. Стержень отклонили на 90° от положения равновесия и отпустили. Определить скорость u нижнего конца стержня в момент прохождения положения равновесия.
Ответ: 
8. Кинетическая энергия электрона равна 1МэВ. Определить скорость электрона .
Ответ: 
Контрольное задание №1
101. Пассажир электропоезда, движущегося со скоростью 15 м/с, заметил, что встречный поезд длиной 210 м прошел мимо него за 6,0 с. Определить скорость встречного поезда.
102. При неподвижном эскалаторе метрополитена пассажир поднимается за t1=120 с, а по движущемуся при той же скорости относительно ступенек – за t2=30 с. Определить время подъема пассажира, неподвижно стоящего на движущемся эскалаторе.
103. Определить скорость моторной лодки относительно воды, если при движении по течению реки её скорость 10 м/с, а при движении против течения – 6,0 м/с. Чему равна скорость течения воды в реке?
104. Скорость поезда, при торможении двигающегося равнозамедленно, уменьшается в течение 1 мин от 40 км/ч до 28 км/ч. Найти ускорение поезда и расстояние, пройденное им за время торможения.
105. Движение материальной точки задано уравнением x=at+bt2+ct3, где
a=5 м/с, b=0,2 м/с2, с=0,1 м/с3. Определить скорость точки в момент времени t1=2 с, t2=4 с, а также среднюю скорость в интервале времени от t1 до t2.
106. Скорость материальной точки, движущейся вдоль оси X, определяется уравнением uX = 0,2-0,1t. Найти координату точки в момент времени t=10 с, если в начальный момент времени она находилась в точке x0=1 м.
107. Самолет для взлета должен иметь скорость 100 м/с. Определить время разбега и ускорение, если длина разбега 600 м; движение самолета при этом считать равноускоренным.
108. Автомобиль движется со скоростью u1=25 м/с. На пути S=40 м производится торможение, после чего скорость уменьшается до u2=15 м/с. Считая движение автомобиля равнозамедленным, найти модуль ускорения и время торможения.
109. Первую половину пути тело двигалось со скоростью u1 = 2 м / с, вторую половину пути - со скоростью u2 = 8 м / с. Определить среднюю скорость движения.
110.Точка прошла половину пути со скоростью 10 км/ч. Оставшуюся часть пути она половину времени двигалась со скоростью 18 км/ч, а последний участок - со скоростью 25,2 км/ч. Найти среднюю скорость движения точки.
111. Определить угловое ускорение маховика, частота вращения которого за время N=20 полных оборотов возросла равномерно от n0=1 об/c до n=5 об/с.
112. Определить зависимость угловой скорости и углового ускорения от времени для твердого тела, вращающегося вокруг неподвижной оси z по закону j=at-bt2, где a=20 рад/с, b=1 рад/с2. Каков характер движения этого тела? Построить графики зависимости угловой скорости и углового ускорения от времени.
113. Колесо радиусом R=10 см вращается с постоянным угловым ускорением e=3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость; 2) линейную скорость; 3) тангенциальное ускорение; 4) нормальное ускорение; 5) полное ускорение.
114. Твёрдое тело вращается вокруг неподвижной оси по закону
j = 6,0 t -2,0 t3. Найти средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки.
115. Вентилятор вращается с частотой 600 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Какое время прошло с момента выключения вентилятора до его полной остановки?
116. Колесо вращается с угловым ускорением 2 рад/с2. Через время 0,5 с после начала движения полное ускорение точек на ободе колеса равно 0,15 м/с2. Найти радиус колеса.
117. Велосипедное колесо вращается с частотой n=5 c-1 . Под действием сил трения оно остановилось через Dt=1 мин. Определить угловое ускорение и число оборотов, которое сделало колесо за это время.
118. Ось с двумя параллельными бумажными дисками, расположенными на расстоянии 0,5 м друг от друга, вращается с частотой 1200 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; пробоины в дисках смещены друг относительно друга на угол 15о. Найти скорость пули. Силой тяжести, действующей на пулю пренебречь.
119. Движение точки по окружности радиусом 4 м задано уравнением
S = 10 - 2 t + t2. Найти тангенциальное, нормальное и полное ускорения точки в момент времени 2 с.
120. Точка движется по окружности радиусом 2 м согласно уравнению S = 2 t3. В какой момент времени нормальное ускорение точки будет равно тангенциальному? Чему будет равно полное ускорение точки в этот момент времени?
121. Тело скользит по наклонной плоскости, составляющей с горизонтом угол a=45°. Зависимость пройденного телом пути S от времени t задана уравнением S=Ct2, где С=1,73 м/с2. Найти коэффициент трения k тела о плоскость.
122. Тело массой m=0,5 кг движется так, что зависимость координаты тела от времени t дается уравнением X=Asin(wt), где А=5 см и w=p рад/с. Найти силу F, действующую на тело через время t=(1/6) с после начала движения.
|
|
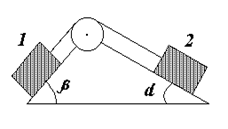
123. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы a=30° и b=45°. Гири 1 и 2 одинаковой массы m1=m2=1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
124. Самолёт делает «мёртвую петлю » радиусом 500 м с постоянной скоростью 360 км/ч. Найти вес летчика массой 70 кг в нижней, верхней и средней точках петли.
125. К пружинным весам подвешен блок. Через блок перекинули шнур, к концам которого привязали грузы массой 1,5 кг и 3 кг. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь.
126. Наклонная плоскость, образующая угол 25о с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения тела о плоскость.
127. На автомобиль массой 1т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью:
а ) в гору с уклоном 1 м на каждые 25 м пути; б ) под гору с тем же уклоном.
128. На столе стоит тележка массой m1=4 кг. К тележке привязан один конец шнура, перекинутого через блок. С каким ускорением будет двигаться тележка, если к другому концу шнура привязать гирю массой m2=1 кг?
129. Аэростат массой m начал опускаться с постоянным ускорением а. Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением воздуха пренебречь.
130. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол 15о с горизонтом. Найти коэффициент трения, если время подъёма тела оказалось в 2 раза меньше времени спуска.
131. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого J=50 кг×м2 и радиус R=20 см. Момент сил трения вращающегося блока MТР=98,1 Н×м. Найти разность сил натяжения нити Т1-Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением
e=2,36 рад/с. Блок считать однородным диском.
132. На барабан массой m0=9 кг намотан шнур, к концу которого привязан груз массой m=2 кг. Найти ускорение a груза. Барабан считать однородным цилиндром. Трением пренебречь.
Похожие работы
... значениями этих параметров, чтобы определить предельные значения и шаг расчёта рассчитываемых параметров. Заключение Хочется выразить уверенность, что в следующих версиях курса "Открытая физика" количество компьютерных моделей будет расти, их функциональные возможности станут разнообразнее, а пределы изменения числовых значений параметров, описывающих эксперименты, будут расширены. Надеемся, что ...
... это количество вещества, взятая в количестве 1 моля. g - количество вещества или число молей. [g]= моль [m]= кг/моль Билет № 7 1. Важным понятием в молекулярной физике и термодинамике является понятие термодинамической системы, к рассмотрению которого мы и переходим. 1.Термодинамической системой (или просто системой) называют совокупность большого числа молекул, атомов или ионов ...
... что разрешало противоречие между результатами Гей-Люссака и Дальтона. Успехи учения об атомно-молекулярном строении вещества, в особенности, газов, безусловно, оказало влияние на становление термодинамики и молекулярной физики и способствовало развитию механической теории теплоты. Во второй половине 18 века господствовала теория теплорода, но уже в начале 19 века она стала уступать свои позиции ...
... : Будем считать величину , измеряемую в энергетических единицах, прямо пропорциональной температуре , выражаемой в градусах: , где - коэффициент пропорциональности. Коэффициент , в честь австрийского физика Л.Больцмана называется постоянной Больцмана. Следовательно, . Температура, определяемая этой формулой, не может быть отрицательной. Следовательно, наименьшим возможным значением температуры ...
0 комментариев