Навигация
Применение пределов в экономических расчетах
6.2 Применение пределов в экономических расчетах
Сложные проценты
В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал и т. д.). Время - дискретная переменная. В некоторых случаях - в доказательствах и расчетах, связанных с непрерывными процессами, возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов:
S = P(1 + i)n. (6.16)
Здесь P - первоначальная сумма, i - ставка процентов (в виде десятичной дроби), S - сумма, образовавшаяся к концу срока ссуды в конце n-го года. Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S - P называются дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной, величиной S. Имеем:
P = ![]() Þ
Þ ![]() P =
P = ![]()
![]() = 0.
= 0.
Таким образом, при очень больших сроках платежа современная величина последнего будет крайне незначительна.
В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется прежде всего тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процессов более адекватно, чем на основе дискретных. Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году:
S =P (1 + i/m) mn.
Наращенная сумма при дискретных процессах находится по этой формуле, здесь m - число периодов начисления в году, i - годовая или номинальная ставка. Чем больше m, тем меньше промежутки времени между моментами начисления процентов. В пределе при m ®¥ имеем:
`S = ![]() P (1 + i/m) mn = P
P (1 + i/m) mn = P![]() ((1 + i/m) m) n.
((1 + i/m) m) n.
Поскольку ![]() (1 + i/m) m = e i, то `S = P e in.
(1 + i/m) m = e i, то `S = P e in.
При непрерывном наращении процентов применяют особый вид процентной ставки - силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номинальной ставки процентов. Для того, чтобы отличить ставки непрерывных процентов от ставки дискретных процентов, обозначим первую через d, тогда `S = Pe![]() .
.
Сила роста d представляет собой номинальную ставку процентов при m®¥. Множитель наращения рассчитывается с помощью ЭВМ или по таблицам функции.
Потоки платежей. Финансовая рента
Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой. Ренты делятся на годовые и р-срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами.
Пример 3.13. Пусть в конце каждого года в течение четырех лет в банк вносится по 1 млн. рублей, проценты начисляются в конце года, ставка - 5% годовых. В этом случае первый взнос обратится к концу срока ренты в величину 10 6 ´ 1,053 так как соответствующая сумма была на счете в течение 3 лет, второй взнос увеличится до 10 6 ´ 1,052, так как был на счете 2 года. Последний взнос процентов не приносит. Таким образом, в конце срока ренты взносы с начисленными на них процентами представляют ряд чисел: 10 6 ´ 1,053; 10 6 ´ 1,052; 10 6 ´ 1,05; 10 6. Наращенная к концу срока ренты величина будет равна сумме членов этого ряда. Обобщим сказанное, выведем соответствующую формулу для наращенной суммы годовой ренты. Обозначим: S - наращенная сумма ренты, R - размер члена ренты, i - ставка процентов (десятичная дробь), n - срок ренты (число лет). Члены ренты будут приносить проценты в течение n - 1, n - 2,..., 2, 1 и 0 лет, а наращенная величина членов ренты составит
R (1 + i)n - 1, R (1 + i)n - 2,..., R (1 + i), R.
Перепишем этот ряд в обратном порядке. Он представляет собой геометрическую прогрессию со знаменателем (1+i) и первым членом R. Найдем сумму членов прогрессии. Получим: S = R´((1 + i)n - 1)/((1 + i) - 1) = = R´((1 + i)n - 1)/ i. Обозначим S n; i =((1 + i)n - 1)/ i и будем называть его коэффициентом наращения ренты. Если же проценты начисляются m раз в году, то S = R´((1 + i/m)mn - 1)/((1 + i/m) m - 1), где i - номинальная ставка процентов.
Величина a n; i =(1 - (1 + i) - n)/ i называется коэффициентом приведения ренты. Коэффициент приведения ренты при n ®¥ показывает, во сколько раз современная величина ренты больше ее члена:
![]() a n; i =
a n; i = ![]() (1 - (1 + i) - n)/ i =1/i.
(1 - (1 + i) - n)/ i =1/i.
Пример 3.14. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено - она выплачивается в течение бесконечного числа лет. Вечная рента не является чистой абстракцией - на практике это некоторые виды облигационных займов, оценка способности пенсионных фондов отвечать по своим обязательствам. Исходя из сущности вечной ренты можно полагать, что ее наращенная сумма равна бесконечно большой величине, что легко доказать по формуле: R´((1 + i)n - 1)/ i ® ¥ при n ® ¥.
Коэффициент приведения для вечной ренты a n; i ® 1/i, откуда A = R/i, т. е. современная величина зависит только от величины члена ренты и принятой ставки процентов.
Похожие работы
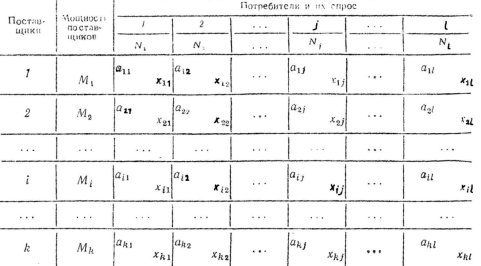
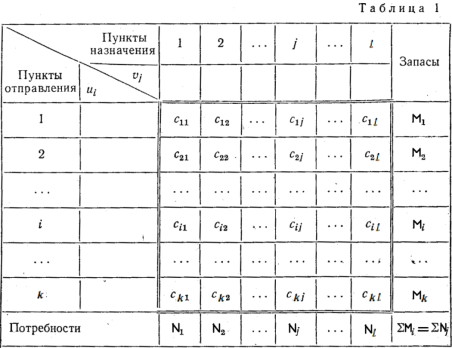
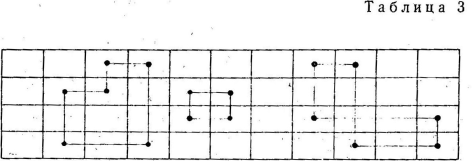
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... признакам следует выделить два основных вида игр, несущих наибольшую образовательную нагрузку, так как все остальные являются производными от них. Этими видами являются инновационные игры и ансамблевые игры. Имитационные или ролевые игры позволяют обучать персонал практически с нуля, в то время как два предыдущих вида больше связаны с развивающим обучением. Назначение деловых игр Деловая ...
... из остальных факторов мало что удастся сделать. Когда я поступил в корпорацию "Крайслер", то взял с собой мои записные книжки из компании "Форд", в которых была отражена служебная карьера нескольких сот фордовских менеджеров. После увольнения я набросал подробный перечень того, что не хотел оставлять в кабинете. Эти записные книжки в черных переплетах, несомненно, принадлежали мне, но можно было ...
... . научн. картине мира, кот. дает естествознание. Необходимость применения естствено научных методов и законов в практической деят-ти гуманитарных специальностей и привело к постановке того курса, кот. мы будем изучать: Физика для гуманитариев. (38) Связь между разделами естествознания. Слово естествознание представляет из себя сочетание 2х слов: естество (природа) и знание. В настоящее время ...
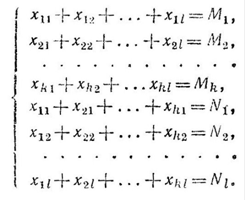

0 комментариев