Линии на плоскости
Матрицы и определители
Определители
Ранг матрицы
Системы линейных уравнений
Метод Гаусса
Системы линейных уравнений общего вида
Использование систем линейных уравнений при решении экономических задач
Предел функции
Применение пределов в экономических расчетах
Производная
Предельный анализ в экономике. Эластичность функции
Экстремум функции
Неопределенность вида ¥/¥. Второе правило Лопиталя
Интегралы
Дифференциальные уравнения
Разностные уравнения
Навигация
Разностные уравнения
Высшая математика для менеджеров
149274
знака
13
таблиц
5
изображений
10. Разностные уравнения
На практике простейшие разностные уравнения возникают при исследовании например величины банковского вклада. Эта величина является переменной Yx, представляющей сумму, которая накапливается по установленному закону при целочисленных значениях аргумента x. Пусть сумма Yo положена в банк при условии начисления 100 r сложных процентов в год. Пусть начисление процентов производится один раз в год и x обозначает число лет с момента помещения вклада (x = 0, 1, 2,...). Обозначим величину вклада по истечении x лет через Yx. Мы получаем
Yx = (1+r)Yx-1.
Если начальная сумма составляет Yo, мы приходим к задаче отыскания решения полученного разностного уравнения, подчиненного начальному условию Yx = Yo при x = 0. Полученное разностное уравнение содержит Yx и значение этой переменной на один год раньше, т.е. Yx-1; в данном случае аргумент x явно не входит в разностное уравнение.
Вообще говоря, обыкновенное разностное уравнение устанавливает связь между значениями функции Y = Y(x), рассматриваемой для ряда равноотстоящих значений аргумента x, но можно без ограничения общности считать, что искомая функция определена для равноотстоящих значений аргумента с шагом, равным единице. Таким образом, если начальное значение аргумента есть x, то ряд его равноотстоящих значений будет x, x+1, x+2,... и в обратном направлении: x, x-1, x-2,.... Соответствующие значения функции будем обозначать Yx,Yx+1,Yx+2,... или Yx, Yx-1, Yx-2,.... Определим так называемые разности различных порядков функции Yx с помощью следующих формул:
Разности первого порядка
D Yx = Yx+1 - Yx,
D Yx+1 =Yx+2 - Yx+1,
DYx+2 = Yx+3 - Yx+2,
... ... ... ... ...
Разности второго порядка
D2Yx= DYx+1 - D Yx,
D2Yx+1= D Yx+2 - DYx+1,
D2Yx+2= D Yx+3 - DYx+2,
... ... ... ... ...
Разности третьего порядка
D3Yx= D2Yx+1 - D2Yx,
D3Yx+1= D2Yx+2 - D2Yx+1,
... ... ... ... ...
Обыкновенным разностным уравнением называется уравнение, связывающее значения одного независимого аргумента x, его функцииYx и разностей различных порядков этой функции DYx, D2Yx, D3Yx,.... Такое уравнение можно записать в общем виде следующим образом:
j(x, Yx, DYx, D2Yx D3Yx, DnYx) = 0, (10.1)
которое по форме аналогично дифференциальному уравнению.
Порядком разностного уравнения называется порядок наивысшей разности, входящей в это уравнение. Разностное уравнение (10.1) часто удобнее записать, пользуясь не разностями неизвестной функции, а ее значениями при последовательных значениях аргумента, то есть выразить DYx, D2Yx, D3Yx,... через Yx, Yx+1, Yx+2,.... Уравнение (10.1) можно привести к одной из двух форм:
y(x, Yx, Yx+1,...,Yx+n) = 0, (10.2)
x(x, Yx, Yx-1,...,Yx-n) = 0. (10.3)
Общее дискретное решение Yx обыкновенного разностного уравнения n-го порядка представляет функцию x (x = 0, 1. 2,...), содержащую ровно n произвольных постоянных:
Yx = Y(x, C1, C2,..., Cn).
Паутинообразная модель. Пусть рынок какого-либо отдельного товара характеризуется следующими функциями спроса и предложения:
D = D(P), S = S(P).
Для существования равновесия цена должна быть такой, чтобы товар на рынке был распродан, или
D(P) = S(P).
Цена равновесия `P задается этим уравнением (которое может иметь множество решений), а соответствующий объем покупок-продаж, обозначаемый через `X, - следующим уравнением:
`X = D (`P) = S(`P).
Динамическая модель получается при наличии запаздывания спроса или предложения. Простейшая модель в дискретном анализе включает неизменное запаздывание или отставание предложения на один интервал:
Dt = D (Pt) и St = S (Pt-1).
Это может случиться, если для производства рассматриваемого товара требуется определенный период времени, выбранный за интервал. Действие модели таково: при заданном Pt-1 предшествующего периода объем предложения на рынке в текущем периоде будет S (Pt-1), и величина Pt должна установиться так, чтобы был куплен весь объем предложенного товара. Иными словами, Pt и объем покупок-продаж Xt характеризуются уравнением:
Xt = D (Pt) = S (Pt-1).
Итак, зная исходную цену Po, с помощью этих уравнений мы можем получить значения P1 и X1. Затем, используя имеющуюся цену P1, из соответствующих уравнений получим значения P2 и X2 и т.д. В общем изменение Pt характеризуется разностным уравнением первого порядка (одноинтервальное отставание):
D (Pt) = S (Pt-1).
Решение можно проиллюстрировать диаграммой, представленной на рис.5, где D и S - соответственно кривые спроса и предложения, а положение равновесия (со значениями `P и `X) соответствует точке их пересечения Q. Цена в начальный момент времени равна Po. Соответствующая точка Qo на кривой S дает объем предложения в период 1. Весь этот предложенный объем товара раскупается при цене P1, заданной точкой Q1 на кривой D с той же ординатой (X1), что и Qo. Во второй период времени движение происходит сначала по вертикали от точки Q1 к точке на кривой S, дающей X2, а затем по горизонтали - к точке Q2 на кривой D. Последняя точка характеризует P2. Продолжение этого процесса и дает график паутины, показанный на рис. 5. Цены и объемы (покупок - продаж) в последовательные периоды времени являются соответственно координатами точек Q1, Q2, Q3,... на кривой спроса D. В рассматриваемом случае последовательность точек стремится к Q. При этом точки поочередно располагаются на левой и правой стороне от Q. Следовательно, и значения цены Pt стремятся к `P, располагаясь поочередно по обе стороны от`P. Точно так же обстоит дело и с объемами покупок - продаж (X t).
Решение можно получить алгебраически для случая линейных функций спроса и предложения: D = a +aP, S = b +bP. Значения равновесия `P и `X будут заданы уравнениями
`X = a +a`P = b +b`P,
то есть
`P = (a - b)/(b - a), `X = (ba - ab)/(b - a). (10.4)
Дискретная динамическая модель задается уравнением
X t = a +aP t = b +bP t-1. (10.5)
Ищем сначала решение, дающее равновесие. Для этого положим P t = `P, X t = `X для всех значений t:
`X = a +a`P = b +b`P. (10.6)
Получаем те же значения `P и `X, что и в (10.4). Следовательно, если в каком-либо периоде существовали цены и объемы, обеспечивающие равновесие, то в динамической модели (10.5) они сохранятся и в последующих периодах.
Вычтем уравнение (10.6) из (10.5) и положим р t = P t -`P, x t = X t -`X. Тогда
x t = aр t = bр t-1. (10.7)
Уравнения (10.7) аналогичны (10.5), за исключением того, что они описывают отклонения от уровней равновесия (теперь уже известно, что таковые существуют). Оба эти уравнения являются разностными уравнениями первого порядка. Положим c = b/a и подставим его в уравнение (10.7), так что разностное уравнение относительно р t будет
р t = c р t-1. (10.8)
При данном значении р o в момент t = 0 из (10.8) получаем решение:
р t = рo c t,
или
P t = `P + (Po - `P) c t.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Аллен Р. Математическая экономия. М.: Изд-во иностранной литературы, 1963.
2. Баврин И. И., Матросов В. Л. Общий курс высшей математики. М.: Просвещение, 1995.
3. Белинский В. А., Калихман В. А., Майстров Л. Е., Митькин А. М. Высшая математика с основами математической статистики. М.: Высшая школа, 1965.
4. Высшая математика: Общий курс / Под ред. А. И. Яблонского. Минск: Вышейш. школа, 1993.
5. Ланкастер К. Математическая экономика. М.: Советское радио, 1972.
6. Макконелл К., Брю С. Экономикс: принципы, проблемы, политика. М.: Республика, 1992. Т. 1-2.
7. Математика и кибернетика в экономике: Словарь - справочник / Под ред. Н. П. Федоренко. М.: Экономика, 1975.
8. Минорский В. П. Сборник задач по высшей математике. М.: Наука, 1987.
9. Рублев А. Н. Линейная алгебра. М.: Высшая школа, 1968.
10. Сборник задач и упражнений по высшей математике: Общий курс: Учеб. пособие / А. В. Кузнецов, Д. С. Кузнецова, Е. И. Шилкина и др. - Минск: Вышейш. шк., 1994.
11. Сборник задач по математическому анализу. Предел, непрерывность, дифференцируемость / Л. Д. Кудрявцев, А. Д. Кутасов, В. И. Чехлов, М. И. Шабунин; Под ред. Л. Д. Кудрявцева. - М.: Наука, 1984.
12. Тышкевич Р. И., Феденко А. С. Линейная алгебра и аналитическая геометрия. Минск: Вышейш. школа, 1968.
13. Фихтенгольц Г. М. Основы математического анализа. М.: Наука, 1968. Т. 1-2.
14. Четыркин Е. М. Методы финансовых и коммерческих расчетов. М.: Дело, Business Речь, 1992.
15. Шипачев В. С. Основы высшей математики / Под ред. А. Н. Тихонова. М.: Высш. шк., 1994.
16. Mathematische Proрadeutik fur Wirtshaftswissenschaftler / W. Wetzel, Н. Skarabis, P. Naeve, Н. Buening. Berlin, New York: Walter de Gruyter, 1981.
17. Mathematik fur Wirtshafts-Kaufleute / E. Forster, Н. Korth. Munchen: Wilhelm Нeyne Verlag, 1976.
ОГЛАВЛЕНИЕ
| ПРЕДИСЛОВИЕ ................................................................................................. | 3 |
| I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ................................................................ | 5 |
| 1. Векторы ..................................................................................................... | 5 |
| 2. Линии на плоскости .................................................................................. | 7 |
| 3. Плоскость и прямая в пространстве ........................................................ | 17 |
| II. ЛИНЕЙНАЯ АЛГЕБРА .................................................................................. | 21 |
| 4. Матрицы и определители ......................................................................... | 21 |
| 4.1. Матрицы. Операции над матрицами .............................................. | 21 |
| 4.2. Определители ................................................................................... | 24 |
| 4.3. Ранг матрицы ................................................................................... | 28 |
| 4.4. Обратная матрица ............................................................................ | 30 |
| 5. Системы линейных уравнений ................................................................. | 33 |
| 5.1. Критерий совместности .................................................................. | 33 |
| 5.2. Метод Гаусса ................................................................................... | 35 |
| 5.3. Формулы Крамера ........................................................................... | 36 |
| 5.4. Матричный метод ............................................................................ | 38 |
| 5.5. Системы линейных уравнений общего вида .................................. | 39 |
| 5.6. Использование систем линейных уравнений при решении экономических задач ............................................................................. | 44 |
| III. МАТЕМАТИЧЕСКИЙ АНАЛИЗ .................................................................. | 50 |
| 6. Предел функции ........................................................................................ | 50 |
| 6.1. Предел последовательности и функции. Теоремы о пределах ...... | 50 |
| 6.2. Применение пределов в экономических расчетах ......................... | 57 |
| 7. Производная .............................................................................................. | 60 |
| 7.1. Производная, правила и формулы дифференцирования ............... | 60 |
| 7.2. Предельный анализ в экономике. Эластичность функции ............ | 64 |
| 7.3. Экстремум функции ........................................................................ | 66 |
| 7.4. Раскрытие неопределенностей. Правило Лопиталя ....................... | 67 |
| 7.5. Частные производные. Метод наименьших квадратов ................. | 68 |
| 8. Интегралы ................................................................................................. | 76 |
| 8.1. Основные методы интегрирования ................................................. | 76 |
| 8.2. Использование интегралов в экономических расчетах ................. | 81 |
| 9. Дифференциальные уравнения ................................................................ | 83 |
| 10. Разностные уравнения ............................................................................ | 90 |
| Список рекомендуемой литературы ................................................................... | 95 |
[
Похожие работы
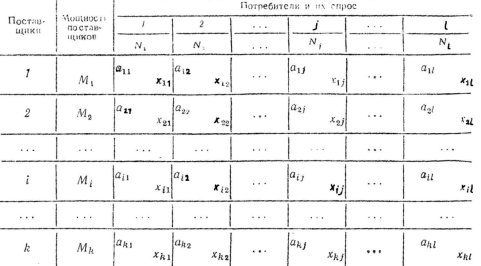
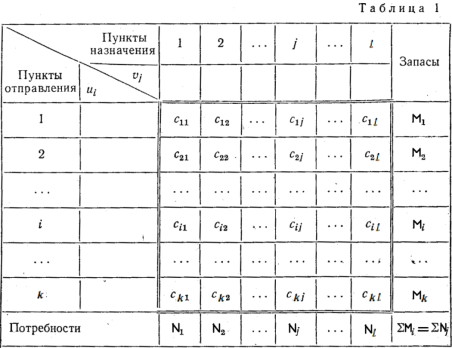
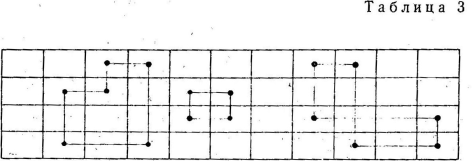
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... признакам следует выделить два основных вида игр, несущих наибольшую образовательную нагрузку, так как все остальные являются производными от них. Этими видами являются инновационные игры и ансамблевые игры. Имитационные или ролевые игры позволяют обучать персонал практически с нуля, в то время как два предыдущих вида больше связаны с развивающим обучением. Назначение деловых игр Деловая ...
... из остальных факторов мало что удастся сделать. Когда я поступил в корпорацию "Крайслер", то взял с собой мои записные книжки из компании "Форд", в которых была отражена служебная карьера нескольких сот фордовских менеджеров. После увольнения я набросал подробный перечень того, что не хотел оставлять в кабинете. Эти записные книжки в черных переплетах, несомненно, принадлежали мне, но можно было ...
... . научн. картине мира, кот. дает естествознание. Необходимость применения естствено научных методов и законов в практической деят-ти гуманитарных специальностей и привело к постановке того курса, кот. мы будем изучать: Физика для гуманитариев. (38) Связь между разделами естествознания. Слово естествознание представляет из себя сочетание 2х слов: естество (природа) и знание. В настоящее время ...
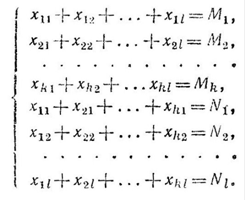
0 комментариев