Навигация
Матрицы и определители
4. Матрицы и определители
4.1 Матрицы. Операции над матрицами
Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
A =  (4.1)
(4.1)
или сокращенно в виде A = (ai j) (i =![]() ; j =
; j = ![]() ). Числа ai j, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (ai j) и B = (bi j) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если ai j = bi j.
). Числа ai j, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (ai j) и B = (bi j) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если ai j = bi j.
Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
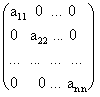 .
.
Если все элементы ai i диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:
E = 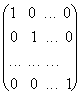 .
.
Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу
AT = ,
,
которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Произведением матрицы А на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l: l A = (l ai j).
Суммой двух матриц А = (ai j) и B = (bi j) одного размера называется матрица C = (ci j) того же размера, элементы которой определяются по формуле ci j = ai j + bi j.
Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Произведением двух матриц А = (ai j) и B = (bj k), где i =![]() , j=
, j=![]() , k=
, k=![]() , заданных в определенном порядке АВ, называется матрица С = (c i k), элементы которой определяются по следующему правилу:
, заданных в определенном порядке АВ, называется матрица С = (c i k), элементы которой определяются по следующему правилу:
c i k = ai 1 b1 k + ai 2 b2 k +... + ai m bm k = ![]() ai s bs k. (4.2)
ai s bs k. (4.2)
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Пример 2.1. Найти произведение матриц А= ![]() и В =
и В = 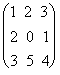 .
.
Решение. Имеем: матрица А размера 2´3, матрица В размера 3´3, тогда произведение АВ = С существует и элементы матрицы С равны с11 = 1×1 +2×2 + 1×3 = 8, с21 = 3×1 + 1×2 + 0×3 = 5, с12 = 1×2 + 2×0 + 1×5 = 7,
с22 =3×2 + 1×0 + 0×5 = 6, с13 = 1×3 + 2×1 + 1×4 = 9, с23 = 3×3 + 1×1 + 0×4 = 10.
AB =![]() , а произведение BA не существует.
, а произведение BA не существует.
Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| М1 | М2 | М3 | |
| 1 | 20 | 35 | 10 |
| 2 | 15 | 27 | 8 |
Решение. Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
А =![]() , В = (50, 70, 130).
, В = (50, 70, 130).
Тогда матрица затрат на перевозки будет иметь вид:
АВT = ![]()
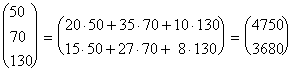 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Пример 2.3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а вектор P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани | |||
| Т1 | Т2 | Т3 | Т4 | |
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
1. Сколько метров ткани каждого типа потребуется для выполнения плана ?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Решение. Обозначим через А матрицу, данную нам в условии, т. е.,
A = 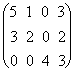 ,
,
тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор X умножить на матрицу А:
X А = (10,15, 23)  =
= ![]() = = (95, 40, 92, 129).
= = (95, 40, 92, 129).
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и вектор CT:
А CT = 
![]() =
=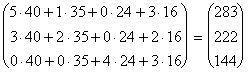 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
X А C T = (10,15,23)![]() =
=![]() .
.
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
X А P T = (95, 40, 92, 129)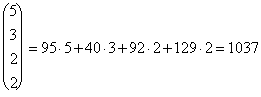 .
.
Итак, X А C T + X А P T = 9472 + 1037 = 10509 (ден. ед).
Похожие работы
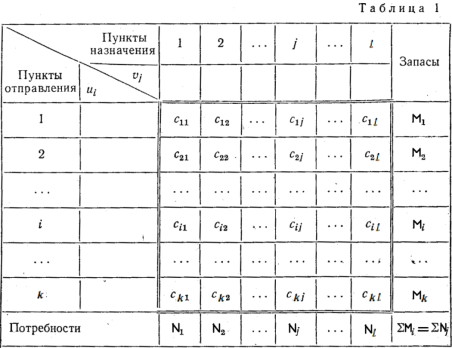
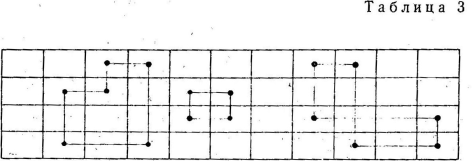
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... признакам следует выделить два основных вида игр, несущих наибольшую образовательную нагрузку, так как все остальные являются производными от них. Этими видами являются инновационные игры и ансамблевые игры. Имитационные или ролевые игры позволяют обучать персонал практически с нуля, в то время как два предыдущих вида больше связаны с развивающим обучением. Назначение деловых игр Деловая ...
... из остальных факторов мало что удастся сделать. Когда я поступил в корпорацию "Крайслер", то взял с собой мои записные книжки из компании "Форд", в которых была отражена служебная карьера нескольких сот фордовских менеджеров. После увольнения я набросал подробный перечень того, что не хотел оставлять в кабинете. Эти записные книжки в черных переплетах, несомненно, принадлежали мне, но можно было ...
... . научн. картине мира, кот. дает естествознание. Необходимость применения естствено научных методов и законов в практической деят-ти гуманитарных специальностей и привело к постановке того курса, кот. мы будем изучать: Физика для гуманитариев. (38) Связь между разделами естествознания. Слово естествознание представляет из себя сочетание 2х слов: естество (природа) и знание. В настоящее время ...
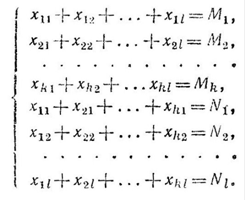

0 комментариев