Трактовка понятия «задача»
Требования к изучению химической задачи и ее место в процессе обучения
Психологическая комфортность. Система задач учитывает наличие разных темпераментов, типов мышления, видов памяти
Неправильное нахождение молекулярной массы вещества
Общие вопросы химической технологии
Вычислить тепловой эффект реакции получения гидроксида кальция
Процесс алюминотермии выражается химическим уравнением
Реакция соединения азота и водорода обратима и протекает по уравнению
Вычислите константу равновесия ниже приведенных реакции, протекающей при стандартных условиях и при 400К
Реакции нулевого порядка. Скорость этих реакций не зависит от концентрации реагирующего вещества n=0. Из уравнений 1.3.1 и 1.3.3 получим следующее
Энергия активации некоторой реакции в отсутствие катализатора равна
Технико-экономические показатели химических производств
> 232 в 3,45 раза => m(Fе) будет > 168 (56 • 3) тоже в 3,45 раза, т. е
Задачи с экологическим содержанием
При производстве серы автоклавным методом неизбежно выделяется около
Электрохимические производства
Производство органических соединений
Творческие и изобретательские задачи
Навигация
Психологическая комфортность. Система задач учитывает наличие разных темпераментов, типов мышления, видов памяти
Методика решения задач по теоретическим основам химической технологии
136540
знаков
1
таблица
2
изображения
7. Психологическая комфортность. Система задач учитывает наличие разных темпераментов, типов мышления, видов памяти.
Система задач - основной ресурс учителя для реализации эффективного образовательного процесса. От качества этого ресурса более чем наполовину зависит успех учащихся при изучении курса. Остальные составляющие успеха заключены в организации их деятельности и управлении этой деятельностью [19, 39].
1.6 Этапы решения задач
Психологами обнаружена закономерность в поведении человека при решении задач. Он разбивает задачу на некоторые число более простых, т.е. ставит пред собой промежуточные вопросы (анализ задачи). Затем приступает к очередной проверке ряда простых задач, накапливая количественную информацию. Решив их, переходит к решению сложной – синтезирует. Таким образом, задачи решаются путем анализа и синтеза в совокупности. Иногда анализ протекает в скрытом виде (решающий провел анализ быстро, по шаблону), в таком случае создается впечатление, что имеет место только синтез. Поэтому цель учителя – не только подобрать задачи к уроку, но и обдумать, как он будет обучать учащихся разбивать подобранные задачи на более простые.
Решение задачи состоит из многих операций, которые связаны между собой и применяются в некоторой логической последовательности. Выявление этих связей и определение последовательности логических и математических операций лежат в основе умения решать задачи.
Решение предполагает поисковую деятельность, включение в этот процесс интеллектуальных операций. С точки зрения дидактики важно иметь в виду и то обстоятельство, что при решении любой задачи (математической, физической, химической и др.) задаются цель, условия и требования к учебно-познавательной деятельности. Естественно предположить существование закономерностей для процесса овладения общей процедурой деятельности. Отсюда вытекает необходимость использования общей методологии решения задач, т.е. объективном процессе интеграции естественнонаучных и математических знаний и умений, неизбежности связи предметных языков. Таким образом, главная дидактическая цель учителя химии при обучении решению расчетных задач: формирование общих логических основ стехиометрических знаний и общепредметных умений на базе общенаучных методов.
В общем виде способ решения химических задач можно представить следующим порядком действий:
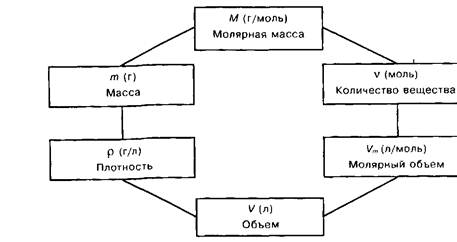
1) краткая запись условия задачи (вначале указывают буквенные обозначения заданных величин и их значения, а затем — искомые величины), которые при необходимости приводятся в единую систему единиц (количественны сторона);
2) выявление химической сущности задачи, составление уравнений всех химических процессов и явлений, о которых идет речь в условии задачи (качественная сторона);
3) соотношения между качественными и количественными данными задачи, т.е. установление связей между приводимыми в задаче величинами с помощью алгебраических уравнений (формул) – законов химии и физики;
4) математические расчеты [15, 57].
1.7 Классификация химических задач
В ходе составления условий простейших задач и их решения необходимо научиться классифицировать задачи, понимать взаимосвязь между различными величинами, характеризующими условие задачи, т. е., прежде чем приступить к решению задачи, необходимо проанализировать ее условие.
На сегодняшний день не существует окончательной едино разработанной классификации химических задач. В учебных пособиях по методике химии, специальных методических пособиях по решению задач и в статьях приводятся различные классификации задач. Общепризнанной является классификация задач на количественные и качественные, которые решаются устным письменным и экспериментальным способом. В свою очередь эти задачи бывают репродуктивными и продуктивными. Репродуктивные задачи – это типовые задачи, при решении которых возможно применение алгоритмов. В этом случае учитель сам объясняет ход их решения. Продуктивные – творческие задачи, в них необходимо самостоятельно найти способы решения. Для этого не достаточно организованного опыта, необходимо качественно иной опыт, заключающийся в умении логически мыслить, анализировать ситуацию в способности к интуитивному решению проблемы как высшего проявления логического мышления [20, 57].
Различаются задачи и упражнения по дидактическим целям. Задачи имеют целью развитие у учащихся умения применять знания химии в различных условиях практики. Упражнения имеют в качестве основных целей формирование навыков, но отдельным операциям, умственным или физическим. Следовательно, знание различия понятий «упражнения» и «задачи» имеет не только теоретическое, но и практическое значение, так как позволяет целесообразно применять упражнения или задачи обучении.
2. Выявление трудностей при решении задач по теоретическим основам химической технологии в рамках изучения курса Прикладная химия
Задачи по химической технологии, составленные и подобранные в настоящей работе, были использованы для проведения контрольной работы по прикладной химии. В апробации участвовали студенты 5 курса специальностей «Химия» с доп. спец. «Биология» и «Биология» с доп. спец. «Химия» (всего 39 студентов). Контрольная работа проводилась на итоговом занятии по прикладной химии. Каждая задача оценивалась по 5-балльной системе в соответствии с тем, насколько полно представлено решение. Оценка за контрольную работу в целом также выставлялась по 5-балльной системе, принятой в ВУЗах.
Практически все студенты справились с задачами (92,3%), в том числе 61,8% на «хорошо» и «отлично» (рис. 1). И действительно, большинство студентов не испытывали трудностей в решении задач. Наиболее успешно были решены задачи по химической технологии с производственным содержанием (металлургия – полностью решили 66,7% студентов, производство органических соединений – 61,5%, рис. 2). Некоторые затруднения вызвало решение задач на темы химическая кинетика и химическое равновесие (полностью эти задачи решили около 40% студентов), возможно, из-за сложного математического аппарата этих задач, где требуется знание основ интегрирования, дифференцирования, возведения в степень и т.д.
Мы проанализировали решение каждого типа задач. Многие студенты не получили высокие баллы за контрольную работу из-за того, что не получили правильные итоговые ответы. Действительно, достаточно большая часть ребят решила задачи «не полностью» (рис. 3, 4). Как правило, такие студенты приводили верные формулы для расчетов, но затруднялись в подстановке численных значений.
Конкретные, наиболее часто встречающиеся ошибки в решении задач представлены в табл. 1.
Таблица 1.| Тема | Результаты контрольной работы, % | Замечания | ||
| Решили полностью | Не решили | Решили не полностью или с ошибками | ||
| Термохимия | 46,2% | 12,8% | 41% | Ошибки связаны в основном с уравнениями химических реакций, студенты забывают расставить коэффициенты, а также ошибки связанные со следствиями из закона Гесса. |
| Химическое равновесие | 41% | 15,4% | 43,6% | Ошибки связаны с нахождением константы равновесия: студенты «переворачивают» формулу для нахождения Кс, а также коэффициенты перед веществами ставят как множители, а не как степень. Не помнят о знаке «-» в уравнении Вант-Гоффа (зависимость константы равновесия от температуры). Также наблюдаются затруднения при нахождении равновесных концентраций, если известна константа равновесия (с использование перемен. х) |
| Химическая кинетика | 38,5% | 20,5% | 41% | Ошибки связаны с определением порядка реакций. Многие студенты забывали о присутствии экспоненты и предэкспоненциального множителя в уравнении Аррениуса. |
| Технико-экономические показатели производств | 59% | 10,3% | 30,7% | Ошибки связаны с неправильным нахождением выхода продукта и с незнанием формул для расчета степени превращения исходных реагентов и селективности. |
| Задачи с экологическим содержанием | 51,3% | 8% | 30,7% | Ошибки связаны с непони-манием сущности задачи, а также ошибки связанные с неправильным переводом м3 в литры, и с неправиль-ным использованием значения массы вещества вместо объема раствора в формуле |
| Металлургия | 66,7% | 7,7% | 25,6% | Ошибки связаны с непра- вильным нахождением mпр и mтеор. В формуле |
| Электрохимические производства | 56,7% | 12,8% | 30,2% | Ошибки связаны с непра- вильным нахождением эквивалента элемента, с неправильным переводом часов в секунды (система СИ). |
| Производство органических соединений | 61,5% | 7,7% | 30,8% | Ошибки связаны с непра- вильным нахождением молекулярной массы вещества, с неправильным определением брутто – формулы вещества |
, например, при нахождении mпр, вместо формулы 
пишут 
, т.е студенты путают значение массы пустой породы с массой чистого вещества.
Общие ошибки:
Похожие работы
... принципа приближения и термодинамической обратимости к экстрактивной ректификации, с одной стороны, и выявить области оптимальности схем экстрактивной ректификации, с другой стороны. Постановка задачи Целью данной работы является разработка технологии разделения азеотропной смеси циклогексан – бензол – этилбензол методом экстрактивной ректификации, обладающей минимальными энергозатратами. Для ...
... , таблица). Метод моделирования позволяет активизировать познавательную деятельность учащихся на уроке. 2.2. Опытно – экспериментальная работа. Анализ ее результатов Изучив теоретические положения по использованию моделирования при решении задач в 5 классе, у автора возникло желание и интерес реализовать это на практике. Для того чтобы доказать или опровергнуть предположение, что ...
... и дидактические основы организации обучения позволяют более доступно объяснять изучаемый материал на уроках физики при изучении темы «Основы электродинамики». Анализ различных технологий позволил составить авторскую технологию развития у учащихся направленности на диалогическое общение при групповой форме обучения. От того, на сколько правильно будет построен процесс обучения при использовании ...
... групп – в виде краткого отчета о проделанной работе (демонстрация рисунков, таблиц). Далее идет обсуждение выступлений; учитель продумывает со своими коллегами трудовое задание [1]. 1.1 Межпредметные связи при решении расчетных задач К изучению математики учащиеся средней школы приступают на 7 лет раньше, чем к изучению химии. За этот период обучения они приобретают значительный объем ...
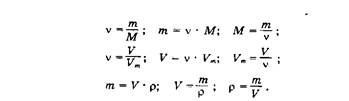
0 комментариев