Трактовка понятия «задача»
Требования к изучению химической задачи и ее место в процессе обучения
Психологическая комфортность. Система задач учитывает наличие разных темпераментов, типов мышления, видов памяти
Неправильное нахождение молекулярной массы вещества
Общие вопросы химической технологии
Вычислить тепловой эффект реакции получения гидроксида кальция
Процесс алюминотермии выражается химическим уравнением
Реакция соединения азота и водорода обратима и протекает по уравнению
Вычислите константу равновесия ниже приведенных реакции, протекающей при стандартных условиях и при 400К
Реакции нулевого порядка. Скорость этих реакций не зависит от концентрации реагирующего вещества n=0. Из уравнений 1.3.1 и 1.3.3 получим следующее
Энергия активации некоторой реакции в отсутствие катализатора равна
Технико-экономические показатели химических производств
> 232 в 3,45 раза => m(Fе) будет > 168 (56 • 3) тоже в 3,45 раза, т. е
Задачи с экологическим содержанием
При производстве серы автоклавным методом неизбежно выделяется около
Электрохимические производства
Производство органических соединений
Творческие и изобретательские задачи
Навигация
Процесс алюминотермии выражается химическим уравнением
Методика решения задач по теоретическим основам химической технологии
136540
знаков
1
таблица
2
изображения
4. Процесс алюминотермии выражается химическим уравнением
8Al + 3 Fe3O4 = 4Al2O3 + 9Fe ΔH<0. Рассчитайте, сколько теплоты выделится при сгорании 1 кг термита.
5. Возможен ли обжиг колчедана массой 1т по следующему уравнению химической реакции 4FeS2 + 11O2 →2 Fe2O3 + 8SO2 ∆H<0
6. Вычислите тепловой эффект образования NH3 из простых веществ, при стандартном условии по тепловым эффектам реакции:
2H2 + O2 = 2H2O(ж) ΔН01 = -571, 68 кДж,
NH3 + 3O2 = 6H2O(ж) + 2N2 ΔН02 = -1530,28 кДж.
7. Стандартный тепловой эффект реакции сгорания этана равен -1560 кДж. Рассчитайте стандартную теплоту образования этана, если известно, что
ΔfН0298 (H2O)= -285,84 кДж/моль и ΔfН0298(СО2) = -396,3 кДж/моль.
8. Вычислите тепловой эффект реакции восстановления оксида железа водородом, пользуясь следующими данными.
FeO + CO = Fe + CO2 ΔН = -13,19 кДж
CO + 1/2O2 = CO2 ΔН = -283,2 кДж
2H2 + 1/2O2 = 2H2O(г) ΔН = -242 кДж
9. Протекание, какой из приведенных реакций восстановления оксида железа (III) наиболее вероятно при 298 К.
Fe2O3(k) + 3H2(г) = 2Fe(к) + 3H2O(к)
Fe2O3(k) + 3С(графит) = 2Fe(к) + 3СO(к)
Fe2O3(k) + 3СО(г) = 2Fe(к) + 3СО2(к)
10. В какой их перечисленных ниже реакций тепловой эффект ΔН0298 будет стандартной теплотой SO3(г)
а) S(г) + 3/2 O2 = SO3(г)
а) S(г) + 1/2 O2 = SO3(г)
а) S(к) + 3/2 O2 = SO3(г)
3.1.2 Химическое равновесие
При протекании химической реакции через некоторое время устанавливается равновесное состояние (химическое равновесие). Слово «равновесие» означает состояние, в котором сбалансированы все противоположно направленные на систему воздействия. Тело, находящееся в состоянии устойчивого равновесия, обнаруживает способность возвращаться в это состояние после какого-либо возмущающего воздействия.
Примером тела, находящегося в состоянии устойчивого равновесия, может служить шарик, лежащий на дне ямки. Если его толкнуть в одну или другую сторону, он вскоре снова возвращается в состояние устойчивого равновесия. В отличие от этого шарик, лежащий на краю ямки, находится в состоянии неустойчивого равновесия — достаточно ничтожного толчка, чтобы он необратимо скатился в ямку.
Оба этих примера являются примерами статического равновесия. В химии, однако, приходится сталкиваться не столько со статическими равновесиями, столько с динамическими («подвижными»). Динамическое равновесие устанавливается, когда оказываются сбалансированными два обратимых или противоположных процесса. Динамические равновесия подразделяют на физические и химические. Наиболее важными типами физических равновесий являются фазовые равновесия. Система находится в состоянии химического равновесия, если скорость прямой реакции равна скорости обратной реакции.
Например, если скорость протекания реакции (константа скорости к1)
k1
А(г) + В(пар) 
АВ(г)
равна скорости обратной реакции (константа скорости k2)
k2
АВ(г) А(г) + В(пар)
то система находится в динамическом равновесии. Подобные реакции называются обратимыми, а их уравнения записывают с помощью двойной стрелки:
k1
А(г) + В(пар) АВ(г)
k2
Реакции, протекающие слева направо, называются прямой, справа налево – обратной.
Нужно подчеркнуть, что реакционная система остается в состоянии динамического равновесия лишь до тех пор, пока система остается изолированной. Изолированной называют такую систему, которая не обменивается с окружающей средой ни веществом, ни энергией.
Состояние химического равновесия обратимых процессов количественно характеризуется константой равновесия. Так, для обратимой реакции общего вида
k1
аA +bB сC + dD (1.2.1)
k2
константа равновесия К, представляющая собой отношение констант скорости прямой и обратной реакций, запишется
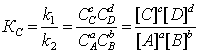(1.2.2)
где, Кс– константа скорости реакции, зависящая от концентрации реагирующих компонентов; Сi или [ i ]- равновесная молярная концентрация i-того компонента;
a, b, c, d – стехиометрические коэффициенты веществ.
В правой части уравнения (1.2.2) стоят концентрации взаимодействующих частиц, которые устанавливают при равновесии, - равновесные концентрации.
Уравнение (1.2.2) представляет собой математическое выражение закона действующих масс при химическом равновесии. Для реакции с участием газов константа равновесия выражается через парциальные давления, а не через их равновесные концентрации. В этом случае константу равновесия обозначают символом Кр.
Рi- равновесные парциальные давления i-того компонента.
Сi - равновесная молярная концентрация компонентов.
a, b, c, d – стехиометрические коэффициенты веществ.
Состояние химического равновесия при неименных внешних условиях теоретически может сохраняться бесконечно долго. В реальной действительности, т.е. при изменении температуры, давления или концентрации реагентов, равновесии может «сместиться» в ту или иную сторону протекания процесса.
Изменения, происходящие в системе в результате внешних воздействий, определяется принципом подвижного равновесия – принципом Ле Шателье – Брауна. При воздействие на равновесную систему, любого внешнего фактора, равновесие в системе смещается в таком направлении, чтобы уменьшить воздействие этого фактора.
1. Влияние давления на равновесие химической реакции (для реакции, проходящей в газовой фазе).
aA + bB cC + dD
- если реакция идет с увеличением количества компонентов a + b < c + d, то повышение давления смещает равновесие химической реакции справа налево.
- если реакция идет с уменьшением количества компонентов a + b > c + d, при увеличении давления сдвиг равновесия произойдет слева направо.
- если количество компонентов одинаково a + b = c + d, то изменение давления не повлияет на положении равновесия.
2. Влияние инертного газа. Введение инертного газа подобно эффекту уменьшения давления (Ar, N2, водяной пар). Инертный газ не участвует в реакции.
3. Влияние изменения концентрации реагирующих веществ. При введение дополнительного количества вещества равновесие химической реакции сместиться в ту сторону где концентрация вещества уменьшается.
4. Влияние температуры на химическое равновесие реакции.
Если к равновесной системе подводится теплота, то в системе происходят изменения, чтобы ослабить это воздействие, т.е. процессы с поглощением теплоты. При экзотермических реакциях снижение температуру сместит равновесие слева направо, а при эндотермических реакциях повышение температуры сместит равновесие справа налево.
Зависимость Кр от температуры – уравнение Вант – Гоффа.
; 
;
(
); lnkT1 – lnkT2 = 
Примеры решения задач
Похожие работы
... принципа приближения и термодинамической обратимости к экстрактивной ректификации, с одной стороны, и выявить области оптимальности схем экстрактивной ректификации, с другой стороны. Постановка задачи Целью данной работы является разработка технологии разделения азеотропной смеси циклогексан – бензол – этилбензол методом экстрактивной ректификации, обладающей минимальными энергозатратами. Для ...
... , таблица). Метод моделирования позволяет активизировать познавательную деятельность учащихся на уроке. 2.2. Опытно – экспериментальная работа. Анализ ее результатов Изучив теоретические положения по использованию моделирования при решении задач в 5 классе, у автора возникло желание и интерес реализовать это на практике. Для того чтобы доказать или опровергнуть предположение, что ...
... и дидактические основы организации обучения позволяют более доступно объяснять изучаемый материал на уроках физики при изучении темы «Основы электродинамики». Анализ различных технологий позволил составить авторскую технологию развития у учащихся направленности на диалогическое общение при групповой форме обучения. От того, на сколько правильно будет построен процесс обучения при использовании ...
... групп – в виде краткого отчета о проделанной работе (демонстрация рисунков, таблиц). Далее идет обсуждение выступлений; учитель продумывает со своими коллегами трудовое задание [1]. 1.1 Межпредметные связи при решении расчетных задач К изучению математики учащиеся средней школы приступают на 7 лет раньше, чем к изучению химии. За этот период обучения они приобретают значительный объем ...
0 комментариев