Навигация
2.1 Операції над ідеалами
Теорема Перетин ab ідеалів a, bÎK є ідеалом кільця K.
Доведення.
З того, що a, bÎI1ÇI2 випливає, що abÎI1, abÎI2. Так як I1 та I2 –ідеали, то (a–b)ÎI1, (a–b)ÎI2 Þ (a–b)ÎI1ÇI2. aÎI1ÇI2 Þ aÎI1, aÎI2.
kÎK Þ kaÎI1, kaÎI2, kaÎI1ÇI2.
Отже, I1ÇI2ÎK.
Доведено.
Слід зауважити, що об’єднання ідеалів не завжди буде ідеалом кільця. Ця властивість поширюється на перетин n ідеалів.
Операції додавання й множення підмножин кільця можна, звичайно, застосувати до ідеалів.
Означення Сумою ідеалів I1, I2 кільця K називається множина I1+I2, яка визначається рівністю
I1+I2 ={a+bï aÎI1, bÎI2}.
Означення Добуток ідеалів I1I2 кільця К теж буде ідеалом кільця К.
Нехай а і b – довільні ідеали кільця К.
Теорема 2. Сума а + b ідеалів a і b кільця К є ідеал цього кільця.
Доведення.
Справді, сума (а1 +b1) + (a2+ b2) будь-яких двох елементів a1+b1 і a2+b2 множини a+b належить до a+b, оскільки (a1+a2)Îa, (b1+b2)Î b, і елемент – (а+b) = (–а) + (–b), протилежний довільно вибраному елементу (a+b)Î(a+b), також належить до a+b, бо (–a)Îa, (–b)Îb.
Отже, а + b є підгрупа адитивної групи кільця K. Крім того, для будь-яких елементів a+bÎa+b і хÎK x (a+b)=xa+xbÎa+b і (a+b) x=ax+bxÎa+b.
Цим теорему доведено.
Теорема 3. Добуток ab ідеалів а і b кільця К. також є ідеал кільця К.
Доведення.
Справді, сума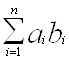 
+
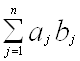будь-яких двох елементів множини аb є, очевидно, елемент цієї самої множини, і елемент 
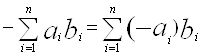, протилежний довільно вибраному елементу 
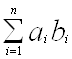Îab, належить до ab. Крім того, для будь-яких
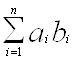Îab і xÎK 
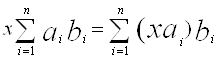Î ab й 
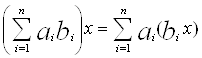Î ab.
Цим теорему доведено.
Таким чином, у множині ідеалів кільця К здійсненні операції додавання й множення. Операція додавання ідеалів – асоціативна і комутативна, а операція множення – асоціативна. Якщо кільце К – комутативне, то операція множення ідеалів також комутативна.
Задачі
№1
Нехай K1 – підкільце кільця K. Довести, що K1ÇI –ідеал кільця K1.
Доведення.
Введемо позначення D=K1ÇI. Покажемо спочатку, що ідеал I, як і будь–який ідеал, містить нуль–елемент кільця K. Справді, оскільки I≠Ø, то в I існує хоч один елемент а. Тоді згідно з першим пунктом означення ідеалу, елемент а–а, тобто 0, теж належить ідеалу I. Оскільки 0ÎK1, 0ÎI, то 0ÎD і тому D≠Ø.
Якщо a, bÎD, то a, bÎK1 і a, bÎI. Згідно з означенням ідеалу і критерієм підкільця, a±bÎI, a±bÎK1, а тому a±bÎD.
Нехай aÎD, bÎK1. Покажемо, що ab і ba належать D. Справді, оскільки DÍK1, то a, bÎK1 і за критерієм підкільця K1 маємо, що
ab, ba ÎK1. (1)
Оскільки DÍI, а I – ідеал кільця K, то для будь–якого елемента aÎDÍI і будь–якого елемента bÎK1ÎK маємо, що
ab, baÎI. (2)
З включень (1) і (2) випливає, щоab, baÎK1ÇI=D.
Отже, D=K1ÇI –ідеал кільця K1.
Доведено.
№2
Чи є ідеалом (лівим або правим) така підмножина
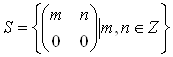
Розв’язання
Перевіримо чи буде множина S лівим ідеалом
Перевіримо множення з ліва
Отже, дана підмножина лівим ідеалом кільця M (2, Z).
Перевіримо чи буде правим ідеалом
Отже правим ідеалом буде.
Відповідь: є правим ідеалом.
3. Факторіальні кільця
3.1 Кільця головних ідеалів та евклідові кільця
3.1.1 Подільність в області цілісності
В теорії кілець особливої уваги заслуговують кільця, які за своїми властивостями досить близькі до кільця цілих чисел. Зокрема, для цих кілець можна розвинути теорію подільності, аналогічну теорії подільності цілих чисел. Ці кільця дістали назву кілець головних ідеалів. Вивченням їх ми і будемо займатись. Але спочатку викладемо деякі загальні відомості, що стосуються подільності в області цілісності з одиницею.
Нехай R – область цілісності з одиницею. Оскільки область цілісності – комутативне кільце, то в ній поняття правого і лівого дільника елемента збігаються і тому означення подільності формулюється так:
Означення 1. Якщо для елементів а і b області цілісності R в R існує такий елемент с, що а == bс, то говорять, що а ділиться на b або b ділить а і пишуть відповідно аM b; b/а або а == 0 (mod b).
Як бачимо, означення 1 є поширенням на область цілісності означення подільності в кільці цілих чисел, яке є конкретним прикладом області цілісності.
З означення 1 випливають такі властивості подільності в області цілісності:
1. "(a, b, cÎR) [aM bÙbM cÞaM c].
2. "(a, b, cÎR) [aM cÙbM cÞ(a+b)M c Ù(a-b)M c].
3. "(a, b, cÎR) [aM b Þ acM b].
4. "(a1, b1, a2, b2,…, an, bn, cÎ R) [a1 M cÙa2 M c Ù… ÙanM c Þ (a1b1 +a2 b2 + … + +an bn) M c].
Ці властивості, як легко бачити, є поширенням на область цілісності відповідних властивостей подільності в кільці цілих чисел.
5. Кожен елемент аÎ R ділиться на будь-який дільник ε одиниці е. Справді, а = ε (ε-1а) і, отже, ε/а.
Похожие работы
... час; організація взаємодії і всебічного забезпечення дій; готовність засобів управління підрозділами. Командири підрозділів військ РХБ захисту зобов’язані своєчасно доповідати старшому командиру про отримане завдання, прийнятому рішенні, результатів застосування противником ЗМУ, виконанні завдання, нових відомостях про противника, радіаційній, хімічній та біологічній (бактеріологічній) обстановц ...
... чим вихідний полімерний матеріал) створюють дратівну дію, їхня присутність у зоні імплантації буде підтримувати вогнище хронічного асептичного запалення. Говорячи про вимоги, висунуті до полімерів медичного призначення, звичайно згадують і необхідність відсутності в них канцерогенної, мутагенної й іншої токсичної дій, хоча зараз ще не ясно, які саме властивості синтетичних полімерів визначають ці ...
... спектру дії Наявність загального родоспецифічного антигена. Все це визначає самостійне положення цих мікроорганізмів серед прокаріот [5]. 3. Характеристика будови та морфології представників роду Chlamydia 3.1 Морфологічні особливості Хламідії є групою прокаріотних мікроорганізмів і мають вид дрібних грамнегативних коків. Добре видні в не зафарбованому стані при мікроскопії ...
... заходів і здійснюється на засадах гласності і суворого додержання вимог законодавства, охорони прав громадян, підприємств та організацій[58][247]. Нарешті зазначимо, що значення адміністративного примусу в правоохоронній діяльності міліції в концентрованому вигляді виявляється в його призначенні та меті. Цей примус слід розглядати як один з найважливіших засобів здійснення державної влади, що ...
0 комментариев