Навигация
Якщо а Î R ділиться на bÎ R, то а ділиться і на bε, де ε – будь-який дільник одиниці
6. Якщо а Î R ділиться на bÎ R, то а ділиться і на bε, де ε – будь-який дільник одиниці.
Справді, з рівності а = bс випливає рівність а == bε (ε-1с) і, отже, bε/а.
7. Кожен з дільників одного з елементів а ÎR і aεÎ R де ε – будь-який дільник одиниці, є дільником і іншого.
Справді, з рівності а = сg випливає рівність aε == с (εg), а з рівності аε = сq – рівність а == с (ε-1q). Отже, якщо с/а, то с/аε, і навпаки.
Всюди далі будемо розглядати елементи області цілісності R, відмінні від нуля.
Означення 2. Елементи а і b області цілісності R називаються асоційованими, якщо кожен з них є дільником іншого:
а = bс, b= аd. (1)
З рівностей (1) випливає, що а = а (сd). Звідси, скоротивши обидві частини рівності на а≠0, дістаємо сd = 1. Отже, с і d є дільники одиниці. Таким чином, якщо а і b – асоційовані елементи, то b = аε, де ε – деякий дільник одиниці. З другого боку, який би ми не взяли дільник одиниці ε, елементи а і аε асоційовані між собою, оскільки а = (аε) ε-1.
Означення 2'. Елементи а і b області цілісності R називаються асоційованими, якщо b= аε, де ε – деякий дільник одиниці.
В кільці цілих чисел, наприклад, асоційованими є кожні два числа т і – т.
Якщо а і b – асоційовані елементи, тобто а = bс і b = аd, то (а) Í (b) і (b) Í (а) і, отже, (а) = (b).
Таким чином, два асоційовані елементи а і b породжують той самий головний ідеал.
Нехай а і b – довільні елементи області цілісності R.
Означення 3. Елемент сÎR називається спільним дільником елементів а і b, якщо кожен з цих елементів ділиться на с. За властивістю 5, всі дільники одиниці е області цілісності R є спільними дільниками елементів а і b. Але в елементів а і b можуть бути й інші спільні дільники. Ми хочемо ввести поняття найбільшого спільного дільника цих елементів. Означення НСД двох цілих чисел, за яким найбільшим спільним дільником називають найбільший із спільних дільників, поширити на область цілісності не можна, оскільки в довільній області цілісності R немає відношення порядку. Проте ми знаємо й інше означення НСД двох чисел, а саме: НСД двох чисел називають такий спільний дільник цих чисел, який ділиться на будь-який інший їхній спільний дільник. Саме це означення ми й поширимо на область цілісності.
Означення 4. Найбільшим спільним дільником елементів а і b області цілісності R називається такий спільний дільник цих елементів, який ділиться на будь-який інший їхній спільний дільник.
Щоб зазначити, що d є найбільший спільний дільник елементів а і b, пишуть а=(а, b).
Якщо також d' = (а, b), то елементи d і d' діляться один на одного і, отже, вони асоційовані. З другого боку, якщо d = (а, b) і ε – будь-який дільник одиниці, то, очевидно, dе = (а, b). Як бачимо, найбільший спільний дільник елементів а і b визначається з точністю до множника ε, що є дільником одиниці.
Означення 5. Елементи а, bÎR називаються взаємно простими, якщо вони не мають спільних дільників, відмінних від дільників одиниці, тобто якщо (а, b) = 1.
Нехай ε – будь-який дільник одиниці і а – довільний елемент області цілісності R. Тоді а = аε• ε-1. З цієї рівності випливає, що всі елементи, асоційовані з елементом а, і всі дільники одиниці ε дільниками елемента а. Їх називають тривіальними, або невласними, дільниками елемента а. Всі інші дільники елемента а, тобто дільники, відмінні від аε і ε, якщо такі існують, називають нетривіальними, або власними. Так, в кільці цілих чисел Z тривіальними дільниками числа 10 є числа ±1, ±10 і нетривіальними – числа ±2, ±5.
Означення 6. Елемент аÎR називається нерозкладним, або простим, якщо він не є дільником одиниці й не має нетривіальних дільників; елемент аÎR називається розкладним, або складеним, якщо він має нетривіальні дільники.
Інакше кажучи, елемент аÎR називається розкладним, якщо його можна записати у вигляді добутку а = bс двох нетривіальних множників b і с; він називається нерозкладним, якщо його не можна записати у вигляді добутку двох нетривіальних дільників, тобто якщо з а = bс завжди випливає, що один з множників b і с є дільник одиниці, а інший – асоційований з а. Так, у кільці цілих чисел Z нерозкладними є числа ±2, ±3, ±5,… (тобто числа прості й протилежні простим); всі інші числа, відмінні від ±1, – розкладні.
Наведемо такі дві властивості нерозкладних елементів.
1. Якщо елемент рÎR нерозкладний, то і будь-який асоційований з ним елемент рε також нерозкладний. Ця властивість випливає з властивості 7 подільності елементів області цілісності R.
2. Якщо а – будь-який, а р – нерозкладний елемент з R, то або а ділиться на р, або а і р – взаємно прості.
Справді, якщо (а, р) = d, то d, як дільник нерозкладного елемента р, або є деякий дільник ε одиниці, або елемент вигляду рε. У першому випадку а і р взаємно прості, в другому – а ділиться на р.
Задачі
№1
Довести, що (-8+3![]() )M (1+2
)M (1+2![]() ) в кільці z [
) в кільці z [![]() ].
].
Доведення.
Поділимо ці гаусові числа, домноживши чисельник і знаменник частки на число спряжене із знаменником
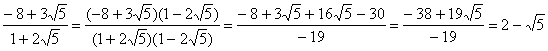 .
.
Так як 2–![]() ÎZ[
ÎZ[![]() ], то (-8+3
], то (-8+3![]() )M (1+2
)M (1+2![]() ).
).
Доведено.
№2
Довести, що в області цілісності К елементи 25–17![]() і 7-
і 7-![]() асоційовані, якщо К=z[
асоційовані, якщо К=z[![]() ].
].
Доведення.
Асоційованість доводиться тим, що одне число ділиться на друге і навпаки.
![]() Оскільки 3–2
Оскільки 3–2![]() Î Z[
Î Z[![]() ], то (25–17
], то (25–17![]() )M(7-
)M(7-![]() ).
).

Бачимо, що і (7-![]() )M(25–17
)M(25–17![]() ).
).
Отже, дані елементи асоційовані.
Доведено.
№3
Довести, що характеристикою області цілісності є або нуль, або просте число.
Доведення.
Нехай K – область цілісності, а е – одиниця кільця К. Якщо me≠0 для жодного натурального числа m1, то характеристика кільця K дорівнює нулю.
Нехай тепер me=0 і m найменше натуральне число, що має цю властивість, тобто m – характеристика кільця K. Тоді m≠1, оскільки е≠0. Якщо m просте число, то твердження задачі доведено.
Нехай m складене число. Тоді існують натуральні числа s і t такі, що 1<s, t<m і m=st. Внаслідок комутативності кільця K маємо
0=me=(st) e=(se) (te).
Крім того, оскільки m – характеристика кільця K і s<m, t<m, то se≠0, te≠0 і тому (se) (te)=me≠0, бо K, як область цілісності, є кільцем без дільників нуля. Отже, ми прийшли до суперечності.
Тому характеристикою області цілісності є або нуль, або просте число.
Доведено.
Похожие работы
... час; організація взаємодії і всебічного забезпечення дій; готовність засобів управління підрозділами. Командири підрозділів військ РХБ захисту зобов’язані своєчасно доповідати старшому командиру про отримане завдання, прийнятому рішенні, результатів застосування противником ЗМУ, виконанні завдання, нових відомостях про противника, радіаційній, хімічній та біологічній (бактеріологічній) обстановц ...
... чим вихідний полімерний матеріал) створюють дратівну дію, їхня присутність у зоні імплантації буде підтримувати вогнище хронічного асептичного запалення. Говорячи про вимоги, висунуті до полімерів медичного призначення, звичайно згадують і необхідність відсутності в них канцерогенної, мутагенної й іншої токсичної дій, хоча зараз ще не ясно, які саме властивості синтетичних полімерів визначають ці ...
... спектру дії Наявність загального родоспецифічного антигена. Все це визначає самостійне положення цих мікроорганізмів серед прокаріот [5]. 3. Характеристика будови та морфології представників роду Chlamydia 3.1 Морфологічні особливості Хламідії є групою прокаріотних мікроорганізмів і мають вид дрібних грамнегативних коків. Добре видні в не зафарбованому стані при мікроскопії ...
... заходів і здійснюється на засадах гласності і суворого додержання вимог законодавства, охорони прав громадян, підприємств та організацій[58][247]. Нарешті зазначимо, що значення адміністративного примусу в правоохоронній діяльності міліції в концентрованому вигляді виявляється в його призначенні та меті. Цей примус слід розглядати як один з найважливіших засобів здійснення державної влади, що ...
0 комментариев