Факторіальність кільця поліномів

3.2.2 Факторіальність кільця поліномів

Теорема. Якщо кільце К факторіальне, то і кільце поліномів К[x] факторіальне.

Доведення.

Нехай К – факторіальне кільце. Доведемо, що будь-який відмінний від нуля необоротний елемент кільця К[x] однозначно з точністю до порядку співмножників і оборотних множників розкладемо в добуток простих множників в K[x]. Спочатку доведемо можливість розкладання на прості множники. Нехай f – довільний ненульовий поліном з K[х]. Якщо f – поліном нульового ступеня, то fÎК. Оскільки кільце K факторіальне, поліном f можна подати у вигляді добутку простих множників у К і, значить, у К[x].Припустимо, що deg f =n>0, і всякий поліном, ступінь якого менше n, розкладемо в добуток простих множників. Нехай

(1) f=dg(x),

де dÎK, g(x) – поліном позитивного степеня, примітивний в К[х]. Якщо поліном g незвідний над К, то, розкладаючи в (1) множник а на прості множники, одержимо розкладання f на прості множники. Якщо ж поліном g(х) звідний в К[х], то його можна подати у вигляді добутку двох поліномів позитивного степеня, меншого, ніж n: g(x)=h(x)j(x).По індуктивному припущенню, h(х) і j(х) можна подати у вигляді добутку простих множників у К[x]. Отже, g, а в силу (1) і f також можна подати у вигляді добутку простих множників.

Доведемо єдиність розкладу. Нехай дані будь-які два розклади f на прості множники в K[x]:

(2) f=p₁…p_kq₁…q_s=p₁¢…p_r¢q₁¢…q_t¢,

де p_i, p_i¢ÎK, q_i, q_i¢ – незвідні, а виходить, і примітивні поліноми позитивного степеня. З (2) випливає, що

(3) p₁…p_k ~p₁¢…p_r¢ в K;

(4) q₁…q_s~q₁¢…q_t¢ в K[x].

Оскільки кільце K факторіальне, то з (3) випливає, що k=r і при відповідній нумерації

(5) p_i~p_i¢ в K для i=1, 2, …, k

Далі, за наслідком 3.6, поліноми q_i і q_i¢ незвідні в кільці F[х]. У силу факторіальності кільця F[х] з (4) випливає, що s=t і при відповідній нумерації

q_i~ q_i¢ в F[х] для i=1,…, s.

Поліноми q_i і q_i¢ незвідні в K[x] і, значить, примітивні в K[х], крім того, ці поліноми асоційовані в F[x]. Отже, вони асоційовані в K[x],

(6) q_i~ q_i¢ в K[х] для i=1,…, s.

У силу (5) і (6) поліном f має однозначний розклад на прості множники в кільці K[x]. Отже, показано, що кільце K[x] факторіальне.

Доведено.

 

Задачі

№1

Довести, що множина I всіх многочленів кільця Z[x], вільний член яких дорівнює парному числу, є ідеалом Z[x]. Чи є цей ідеал головним?

Розв’язання.

Очевидно, що ця множина замкнена відносно віднімання та множення на довільний елемент кільця. Отже, ця множина буде ідеалом.

Візьмемо будь–які елементи

x²+4ÎI, x+2ÎI.

Перевіримо чи x²+4Mx+2.

x²+4=x²–4+8=(x-2) (x+2)+8.

Так як x²+4 не ділиться на x+2 то дана множина I не буде головним ідеалом.

Відповідь: Множина I буде ідеалом, але не головним.

№2

Знайти НСД і НСК таких многочленів:

f(x)=x⁴+2x³–2x-1,

g(x)=(x+1) (x²–x-2)

в кільці Q[x].

Розв’язання.

Розкладемо дані многочлени на множники:

f(x)=x⁴–1+2x(x²–1)=(x²–1) (x²+2x+1)=(x+1)³(x-1),

g(x)=(x+1) (x-2) (x+1)=(x+1)²(x-2).

Очевидно, що

(f, g)=(x+1)²,

[f, g]=(x+1)³(x-1) (x-2).

Відповідь: (f, g)=(x+1)², [f, g]=(x+1)³(x-1) (x-2).

№3

Розкласти на незвідні в полі P множники такий многочлен:

f(x)=x⁴–2x³–27x²–44x+7.

Розв’язання.

Розклад матиме такий вигляд:

f(x)=(x²+bx+1) (x²+cx+7).

f(x)=x⁴+(c+b) x³+(bc+8) x²+(7b+c) x+7.

с=–2-b,

(–2-b) b=–35,

– b²–2b=–35,

b²+2b-35=0,

 

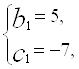
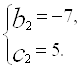
Отже, даний многочлен розкладається таким чином:

f(x)=(x²–7x+1) (x²+5x+7).

Відповідь: f(x)=(x²–7x+1) (x²+5x+7).

3.3 Кільце многочленів від кількох змінних

 

3.3.1 Поняття кільця многочленів від кількох змінних

Означення Кільцем многочленів R[х₁, х₂,…, x_n-1, х_n] від n змінних х₁, х₂,…, x_n-1, х_n над областю цілісності R називається кільце многочленів від змінної x_n над кільцем R[х₁, х₂,…, x_n-1] тобто

R[х₁, х₂,…, x_n-1, х_n] = R[х₁, х₂,…, x_n-1] [x_n] (4)

Це означення має індуктивний характер. При п=1 воно зводиться до означення кільця многочленів від однієї змінної х₁ над областю цілісності R (природно вважати, що при п =1 R[х₁, х₂,…, x_n-1, х_n] =R). Якщо ж уже означено кільце R[х₁, х₂,…, x_n-1] при п ³1, то за допомогою (4) дістаємо означення кільця R[х₁, х₂,…, x_n-1, х_n]. Отже, для довільного натурального п означено кільце многочленів від п змінних х₁, х₂,…, x_n-1, х_n

Теорема Кільце многочленів R[х₁, х₂,…, x_n-1, х_n] над областю цілісності R є область цілісності.

Доведення.

Твердження правильне при п = 1. Припустимо, що воно правильне при п = т і розглянемо кільце R[х₁, х₂,…, x_m, х_m+1]. Згідно з означенням 1, R[х₁, х₂,…, x_m, х_m+1] є кільце многочленів над R_m= R[х₁, х₂,…, x_m]. За припущенням індукції, R, є область цілісності. Отже, R_m[x_m+1]=R[х₁, х₂,…, x_m, х_m+1] є область цілісності. За принципом індукції, R[х₁, х₂,…, x_n-1, х_n] є область цілісності при довільному натуральному п.

Доведено.

Зрозуміло, що коли R – область цілісності з одиницею, то R[х₁, х₂,…, x_n-1, х_n] – область цілісності з одиницею.

Наступна теорема встановлює будову елементів області цілісності R[х₁, х₂,…, x_n-1, х_n].

Теорема 2. Кожний елемент fÎR [х₁, х₂,…, x_n-1, х_n] можна подати у вигляді скінченної суми

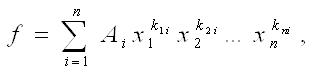A_iÎR, k_ijÎZ₊ (5)

Навпаки, будь-який вираз виду (5) є елементом кільця R[х₁, х₂,…, x_n-1, х_n].

Доведення

Доведення проведемо індукцією по n. При n=1 твердження правильне. Припустимо, що воно правильне при n=m і перевіримо його правильність при n=m+1. За означенням 1, кожний елемент fÎR [х₁, х₂,…, x_m, х_m+1] є многочлен від Х_m=1 над областю цілісності R [х₁, х₂,…, x_m], і тому його можна подати у вигляді суми

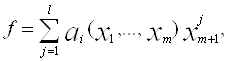
  (6)

За припущенням індукції, кожний многочлен a_j(x₁, …, x_m) від n змінних можна подати у вигляді скінченної суми

, (7)

,

(i=1, 2, …, N_j; s=1, 2, …, m; j=0, 1, 2, …, l).

Підставивши вираз (7) в (6) і виконавши відповідні дії (в розумінні дій у кільці R[х₁, х₂,…, x_m, х_m+1] з урахуванням того, що воно містить R[х₁, х₂,…, x_m] як підкільце), дістанемо скінченну суму виду

, (8)

де B_rÎR (r=1, …, N), бо кожне B_r є якесь з .

Навпаки, кожна сума виду (8) є елемент кільця R[х₁, х₂,…, x_m, х_m+1]: адже будь-який її доданок може розглядатись як многочлен від x_m+1 з коефіцієнтом ÎR[х₁, х₂,…, x_m] й тому й уся сума належить кільцю R[х₁, х₂,…, x_m, х_m+1].

Отже, твердження теореми правильне і при n=m+1, тобто за принципом математичної індукції теорему доведено.

Доведено.

Означення Кожний елемент кільця R[х₁, х₂,…, x_n] називають многочленом від n змінних х₁, х₂,…, x_n над R. і позначають f(х₁, х₂,…, x_n), g(х₁, х₂,…, x_n) і т. п.

Згідно з теоремою 2, будь-який многочлен з R[х₁, х₂,…, x_n] можна подати у формі суми (5)

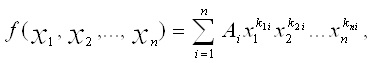 A_iÎR, k_ijÎZ₊ (9)

Кожний доданок цієї суми називають членом многочлена f(х₁, х₂,…, x_n), відповідний елемент A_iÎR – коефіцієнтом члена (і многочлена). Два члени, які відрізняються лише коефіцієнтами, називають подібними; іншими словами, члени подібні, якщо усі змінні входять множниками в ці члени у попарно рівних степенях, наприклад  та . При цьому порядок, в якому записано множники неістотний, тобто

члени , , тощо вважаємо однаковими, рівними між собою. Відповідно до цього, R[х₂, х₁,…, x_n], R[х₃, х₂,…, x₁], R[х₁, х₂,…, x_n] і т. п. є різними формами запису того самого кільця многочленів від змінних х₁, х₂,…, x_n над областю цілісності R.

 

Задачі

№1

Виразити через σ_і такий многочлен

f (x, y)=x³y+y³x+2x²+2y².

Розв’язання.

Основні симетричні многочлени σ₁, σ₂ мають вигляд:

σ₁=x+y,

σ₂=xy.

Виразимо даний многочлен через σ₁, σ₂

f (x, y)=xy(x²+y²)+2 (x²+y²)=(x²+y²) (xy+2)=

=((x+y)²–2xy) (xy+2)=(σ₁–2σ₂) (σ₂+2)=

=σ₁²σ₂+2σ₁²–2σ₂²–4σ₂.

Відповідь: f (x, y)=σ₁²σ₂+2σ₁²–2σ₂²–4σ₂.

№2

Довести, що для S_n=xⁿ+yⁿ, nÎN, при n>2 виконується рекурентне співвідношення

S_k=σ₁S_k–1–σ₂S_k–2.

Доведення.

Доведемо методом математичної індукції.

Перевіримо базу індукції при n=3

S₃=σ₁S₂–σ₂S₁=(x+y) (x²+y²) – xy (x+y)=x³+y³.

Припустимо, що твердження вірне для n=k.

Доведемо, що дане твердження справджується і при n=k+1

S_k+1=σ₁S_k–σ₂S_k–1=(x+y) (x^k+y^k) – xy(x^k–1+y^k–1)=

=x^k+1+xy^k+x^ky+y^k+1–x^ky–xy^k=x^k+1+x^k+1.

Отже, виходячи з математичної індукції твердження доведено.

Доведено.

3.3.2 Факторіальність кільця поліномів від n змінних

Теорема. Нехай К – факторіальне кільце. Тоді кільце поліномів К[х₁,….х_n] від х₁,…., х_n над К також являється факторіальним.

Доведення.

Теорема доводиться індукцією по n. Для n=1 твердження правильне. Припустимо, що кільце поліномів К[х₁,….х_n–1] від х₁,….х_n–1, над К факторіальне. Доведемо, що факторіальним тоді буде і кільце К[х₁,…, х_n].

К[х₁,…, х_n]=К[х₁]… [.х_n]=(К[х₁,….х_n–1]) [x_n].

За індуктивним припущенням, кільце К[х₁,…, х_n–1] факторіальне. Тоді факторіальним є також його розширення (К[х₁,….х_n–1]) [x_n] за допомогою елемента x_n, трансцендентного над кільцем К[х₁,….х_n–1]. Таким чином, кільце поліномів К[х₁,….х_n] факторіальне для довільного натурального n.

Доведено.

Наслідок Кільце поліномів F[х₁,….х_n] над полем F факторіальне.

Задачі

№1

Розкласти на множники найменшого степеня з дійсними коефіцієнтами такий многочлен

f (x, y)=10x⁴–27x³y-110x²y²–27xy³+10y⁴.

Розв’язання.

f (x, y)=10x⁴–27x³y-110x²y²–27xy³+10y⁴=10 (x⁴+y⁴) – 27 (x²+y²)–110x=

=10 [(σ₁²–2σ₂)²–2σ₂²]–27σ₂(σ₁²–2σ₂)–110σ₂²=10σ₁⁴–67σ₁²σ₂–36σ₂².

Розкладемо цей вираз на множники. Для цього знайдемо його корені.

σ₂^′=–2σ₁²,

σ₂^′′=σ₁².

Тоді наш многочлен

f=–36 (σ₂–σ₁²) (σ₂+2σ₁²)=(–36σ₂+5σ₁²) (σ₂+2σ₁²).

f (x, y)=(–36xy+5 (x+y)²) (xy+2 (x+y)²=

=(–36xy+5x²+10xy+5y²) (2x²+3xy+2y²)=

=(5x²–26xy+5y²) (2x²+3xy+2y²).

Розглянемо кожний з цих множників, як квадратний тричлен відносно x

5x²–26xy+5y² x′=5y, x′′=.

2x²+3xy+2y² x′=y, x′′=–2y.

Тоді маємо

f (x, y)=(x+2y) (2x+y) (x-5y) (5x–y).

Відповідь: f (x, y)=(x+2y) (2x+y) (x-5y) (5x–y).

Використана література

1.  Алгебра і теорія чисел, ч. 1. Завало С.Т., Костарчук В.М., Хацет Б.І. Видавниче об’єднання «Вища школа», 1974, 464 с.

2.  Алгебра і теорія чисел, ч. 2. Завало С.Т., Костарчук В.М., Хацет Б.І. Видавниче об’єднання «Вища школа», 1976, 384 с.

3.  Алгебра и теория чисел: Учебное пособие для педагогических институтов.–М.: Высшая школа, 1979, – 559 с., ил.

4.  Збірник задач з теорії чисел. [Навчальний посібник для студентів фізико-математичного факультету] За ред. І.О. Рокіцького, Вінниця, 2001–115 с.

5.  Збірник задач з алгебри. [навчальний посібник для студентів фізико-математичного факультету] За ред. І.О. Рокіцького, Вінниця, 2002–176 с.

6.  Алгебра і теорія чисел: Практикум. Частина 2 /С.Т. Завало, С.С. Левіщенко, В.В. Пилаєв, І.О. Рокіцький. – К.: Вища школа Головне видавництво, 1986. – 364 с.

7.  Збірник задач і вправ з теорії чисел. Є.П. Морокішко. Центр «Магістр-S», 1995 р. 158 с.