F-критерій

1.2 F-критерій

Розглянемо лінійну модель Y =Хβ + ε, в якій матриця X має розмір nр і ранг р, ε ~ N_n(0, σ²I_n). Нехай ми хочемо перевірити гіпотезу H: Аβ = c, де А - відома (qp) - матриця рангу q, а с - відомий (q1) - вектор. Позначимо

RSS = (Y –X)'(Y-X) = (n – p)S²

RSS_H = (Y –X_H)'(Y-X_H)

Де _H=  + (Х'Х)^-1А'[А(Х'Х)^-1А']^-1(с-А), (1.2.1)

і RSS_H - мінімальне значення ε'ε при обмеженнях Аβ = с.

Теорема 1.2.1.

(I) RSS_H - RSS = (А- c)' [А (Х'Х)^-1 А']^-1 (А- c),

(II) М [RSS_H - RSS] = σ²q + (Аβ -с)' [А(Х'Х)^-1А']^-1(Аβ - с).

(III) Якщо гіпотеза Н: Аβ = с справедлива, то статистика

F =

має розподіл Фішера F_q,n-p (F-розподіл з q і n - p ступенями вільності відповідно).

(IV) Якщо с = 0, то статистика F приймає вигляд

F = ,

де Р_H - симетрична і ідемпотентна матриця і Р_НP = PР_Н = Р_Н

Доведення.

(I) Спочатку доведемо тотожність:

||Y - X_H||² = ||Y - X||² + ||X( - _H)||²

Розглянемо

||X( - )||² = (X( - β))'X( - β) = ( - β)'X'X ( - β) = ( - _H + _H - β)'X'X ( - _H + _H - β) =

= ( - _H)'X'X ( - _H) + (_H - β)'X'X (_H - β) =

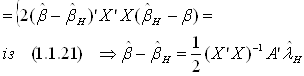
= 2((X'X)^-1A')'X'X(_H - β) = A(X'X)^-1 X'X(_H - β) = A(_H - β) = (A_H - Aβ) = (c – c) = 0= (X(-_H))'X( - _H) + (X(_H - β))'X(_H - β) = ||X( - _H)||² + ||X(_H- β)||².

Далі,

ε'ε = (Y – Xβ)'(Y – Xβ) = ||Y – Xβ||² = (Y - X)'(Y - X) +

+ ( - β)'X'X( - β) = ||Y - X||² + ||X( - β)||²

Підставляємо

||X( - β)||²:

ε'ε = ||Y - X||² + ||X( - _H)||² + ||X( - β)||²

ε'ε досягає мінімального значення при ||X( - β)||² = 0, тобто

X( - β) = 0

β = , Х ≠ 0 (оскільки стовпці Х лінійно незалежні)

Покладаючи в ε'ε β = , знаходимо

||Y - X_H||² = ||Y - X||² + ||X( - _H)||²

Тоді

RSS_H – RSS = (Y - X_H)'(Y - X_H) – (Y - X)'(Y - X) =

= ||Y - X_H||² - ||Y - X||² = ||X( - _H)||² = (X( - _H))'(X( - _H)) =

= ( - _H)'X'X( - _H) =

=  =

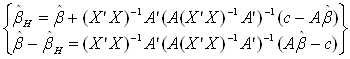= ((X'X)^-1A'(A(X'X)^-1A')^-1(A - c))'X'X((X'X)^-1A'(A(X'X)^-1A')^-1(A - c)) =

= (A - c)'(A(X'X)^-1A')^-1A(X'X)^-1(X'X)(X'X)^-1A'(A(X'X)^-1A')^-1(A - c) =

= (A - c)'(A(X'X)^-1A')^-1(A - c).

(II) Скористаємось лемою.

Нехай Y = Y^(n×1) - випадковий вектор, A^(n×n) = A - симетрична матриця. Якщо MY = θ, DY = ∑, тоді

M(Y'AY) = tr(A∑) + θ'Aθ.

Раніше, доведено, що

 ~ N_p(β, σ²(Х'Х)^-1), A ~ N_q(Aβ, σ²A(Х'Х)^-1A').

Позначимо Z = А - c і В = А(Х'Х)^-1А'. Тоді

M[Z] = M(А – c) = A - c = = Аβ – c і

D[Z] = D(А – c) = D[A] = σ²B

Тоді

M[RSS_H - RSS] = M[Z'В^-1Z] = tr[σ²В^-1В] + (Аβ - с)' В^-1(Аβ - с) =

= tr[σ²I_q] + (Aβ – c)'B^-1(Aβ – c) =

= σ²q + (Aβ – c)'B^-1(Aβ – c). (1.2.2)

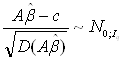
(III) Відомо, що  ~ N_q(β,σ²А(Х'Х)^-1), тоді

A ~ N_q(Aβ, σ²A(Х'Х)^-1A') і

А - с ~ N_q(Aβ - c, σ²A(Х'Х)^-1A'),

, тоді .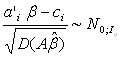

Розглянемо (RSS_H – RSS)/σ²

 = (А - с)' (D[А])^-1(А - с),

Раніше доведено, що RSS/σ² ~  (теорема 1.1.6 (IV)), тоді статистика

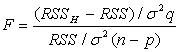
при справедливій гіпотезі Н має вигляд [/q]/[/(n - р)]. Отже, якщо гіпотеза Н справедлива, то F ~ F_q,n-p.

(IV) Нехай у виразі (1.2.1) c = 0, тоді маємо

 = X(_H - (Х'Х)^-1А'[А(Х'Х)^-1А']^-1А) = X -

-  X(Х'Х)^-1А'[А(Х'Х)^-1А']^-1А =

= X(Х'Х)^-1 Х'Y - X(Х'Х)^-1А'[А(Х'Х)^-1А']^-1А(Х'Х)^-1 Х'Y =

={X(Х'Х)^-1X' - X(Х'Х)^-1А'[А(Х'Х)^-1А']^-1А(Х'Х)^-1Х'}Y= (Р-Р₁)Y, (1.2.3)

Тобто

(1.2.4)

де Р_H - симетрична матриця. Спростивши вираз для матриці Р₁, знаходимо, що Р₁ симетрична і ідемпотентна і Р₁Р = РР₁ = Р₁. Звідси одержуємо

 = Р² - Р₁P – РP₁ +  = P - 2P₁ + P₁ = P - P₁ =P_H (1.2.5)

P_HP = (P - P₁)P = P - P₁ = P_H (1.2.6)

і РР_H = Р_H (останнє одержуємо транспонуванням).

Y - X = Y - X(Х'Х)^-1 Х'Y = Y(I - X(Х'Х)^-1 Х') = (I – P)Y.

Тоді

RSS = (Y - X)'(Y - X) = ((I – P)Y)'(I – P)Y =

= Y'(I – P)'(I – P)Y = Y'(I_n - Р)Y

Aналогічно

RSS_H= (Y - X_H)'(Y - X_H) = Y'(I_n – Р_H)Y. (1.2.7)

Таким чином,

RSS_H – RSS = Y'(I_n – Р_H)Y - Y'(I_n - Р)Y = Y'(I – Р_H – I + P)Y = Y'(P – Р_H)Y.

Отже,

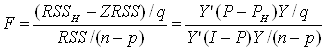
Теорема доведена.

F – критерій для перевірки гіпотези H: Aβ = c.

Гіпотезу H: Aβ = c відхиляють при

і не відхиляють в супротивному разі. Рівень значущості критерію α.

Похожие работы

Соціологічний аналіз молодіжної наркоманії в Україні

Скачать

138713

9

0

... притягають до себе різних кримінальних особистостей. І не випадково саме повії нерідко стають жертвами рекетирів, використовуються організованою злочинністю. Розділ 3. Соціологічний аналіз молодіжної наркоманії в Україні Сьогодні соціологи фіксують вагоме помолодіння різних форм девіантної поведінки. Тому виникає необхідність більш розгорнуто обдивиться проблему молодіжної наркоманії. ...

Статистичний облік природних ресурсів в Україні

Скачать

49793

18

5

... навантаження поділяються на показники антро­погенного та природного навантаження. Щоб оцінити антропо­генне навантаження на довкілля, застосовують показники: ·  видобутку (збору врожаю) окремих природних ресурсів; ·  що характеризують кiлькiсть викидів і скидів забруднюючих речовин та вiдходiв у атмосферне повітря, водні ресурси та в землю; ·  що характеризують кiлькiсть використовуваних ...

Динаміка профілю ризику серцево-судинних захворювань в жіночій популяції

Скачать

56321

2

4

... інгових тестів) та спільно з психотерапевтами коригувати тривожно-депресивні стани. СПИСОК ОПУБЛІКОВАНИХ ПРАЦЬ ЗА ТЕМОЮ ДИСЕРТАЦІЇ 1. Малацківська О.В. Динаміка профілю ризику серцево-судинних захворювань в жіночій популяції за 25-річний період // Кровообіг та гемостаз.– № 3. – 2006. – С. 49-52. 2. Малацківська О.В., Горбась І.М. Зв’язок традиційних факторів ризику серцево-судинних ...

Особливості клініки, діагностики, профілактики та лікування захворювань пародонта у вагітних із акушерською патологією

Скачать

51422

0

0

... А. В. Борисенко, О. О. Шекера // Матеріали ІІІ (Х) з’їзду Асоціації стоматологів України. – Полтава, 2008. – С. 136 АНОТАЦІЯ   Шекера О. О. Особливості клініки, діагностики, профілактики та лікування захворювань пародонта у вагітних із акушерською патологією. – Рукопис. Дисертація на здобуття наукового ступеня кандидата медичних наук за спеціальністю 14.01.22 – стоматологія. – Національний ...