Лінійна одновимірна регресія

1.3 Лінійна одновимірна регресія

Нехай Y_i = β₀ + β₁x_i + ε_i (i = 1,2, …, n) і ми хочемо перевірити гіпотезу H: β₁ = 0. Тоді X = (I_n, x),

, ,

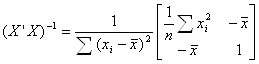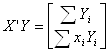
Підставляючи ці вирази у формулу  = (X’X)^-1X’Y, після деяких спрощень одержуємо

₀ = (1.3.1)

 = ₀ + ₁x_i =  (1.3.2)

Нарешті, знаходимо вираз для F- статистики

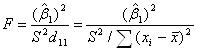(1.3.3)

Де

Помітимо, що з (1.3.4) випливає, що

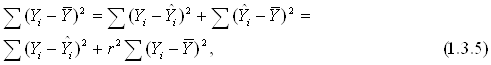
Де

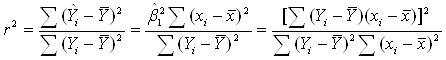
є квадратом вибіркового коефіцієнта кореляції між Y і х. Відношення r є мірою ступені лінійності зв'язку меж Y і х, оскільки, згідно з (1.3.5),

RSS =  (1.3.6)

Отже, чим більше значення г², тим менше RSS і, тим краще підібрана пряма відповідає спостереженням.

1.4 Порівняння прямих регресій. Критерій паралельності прямих. Критерій збігу прямих

Нехай необхідно порівняти K ліній регресій

Y = α_k+ β_kx_k + ε (k =1, 2, ..., K),

де M[ε] = 0 і дисперсії D[ε] = σ² однакові для всіх K ліній. Якщо для k-й лінії є n_k пар спостережень (x_ki, Y_ki ) (i = 1, 2, ..., n_k), то модель приймає вигляд

Y_ki = α_k+ β_kx_ki + ε_ki(k =1, 2, ..., n_k), (1.4.1)

де ε_ki - незалежні випадкові величини з розподілом N(0, σ²).

Введемо позначення Y' = (Y₁₁, Y₁₂, …, Y_1n1, …, Y_Kn1, …, Y_Knk) запишемо модель у вигляді Y = Xγ + ε, де

Тут X -матріца розміру N×2K рангу 2К, а N = .

Використовуючи загальну теорію підрозділу 1.2, можна перевірити будь-яку гіпотезу вигляду Н:Аγ = с. Дві гіпотези такого роду розглядаються нижче.

Критерій паралельності прямих

Розглянемо задачу перевірки паралельності всіх K ліній. Тоді гіпотеза

Н:Аγ = с має вигляд H₁: β₁ = β₂ = . . . = β_K = β, або β₁- β_K = β₂ – β_K = ... = β_K-1 - - β_K= 0. У матричній формі H₁ приймає вигляд

або Аγ = 0, де А-матрица розміру (К- 1)×2K рангу K-1. Використовуючи загальну теорію регресії з q = K-1, n = N і р = 2К, одержуємо, що статистика критерія для перевірки гіпотези H₁, має вигляд

 (1.4.2)

Для знаходження RSS необхідно мінімізувати

S = ε'ε = .

Продиференціюємо S по α_k та β_k

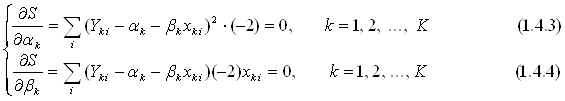
З перших K рівнянь системи знаходимо, що

Підставляємо α_k в (1.4.4)

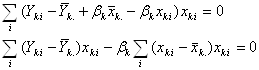
 (1.4.5)

Тоді  Підставляємо оцінки  в S. Знаходимо

RSS =

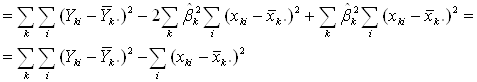 (1.4.6)

Для знаходження  мінімізуємо суму S = відносно α і β. Продиференціюємо S по α_k та β

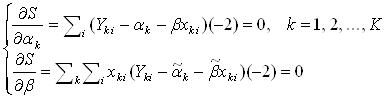 (k = 1, 2, …, K)

З перших K рівнянь системи знаходимо

Підставляємо знайдені α_k в друге рівняння системи

Тоді

Підставляючи оцінки  в S, знаходимо

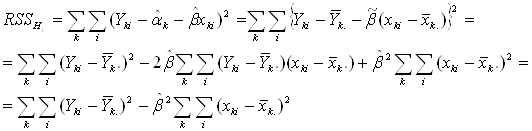
Отже, гіпотезу H₁: β₁ = β₂ = . . . = β_K = β відхиляємо при

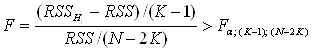
і не відхиляємо в супротивному разі. Рівень значущості критерію α.

Критерій збігу прямих

Для вирішення питання про збіг всіх K ліній регресії розглянемо гіпотезу H₂: α₁ = α₂ = ... = α_K і β₁ = β₁ = ... = β_K, або, що те ж саме, H₂: α₁- α_K = = α₂ - α_K = ... = α_K-1 - α_K = 0 і β₁ - β_K= ... = β_K-1 - β_K = 0.

В матричній формі гіпотеза H₂ приймає вигляд:Aγ = 0, зокрема

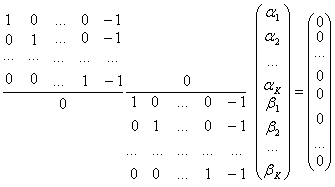
Матриця А має розмір (2K-2) рядків, 2K стовпців (ранг 2М – 2).

F – статистика для перевірки гіпотези H₂ має вигляд

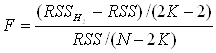(1.4.7)

Знайдемо RSS_H2. Для знаходження RSS_H2 необхідно мінімізувати суму по α і β, одержуємо

Із першого рівняння знаходимо

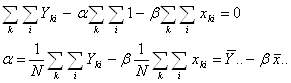
Підставляючи α в перше рівняння системи одержуємо β

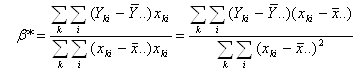
Тоді

Отже,

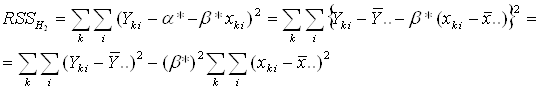
Отже, гіпотезу H₂:α₁ = α₂ = ... = α_K і β₁ = β₁ = ... = β_Kвідхиляємо при

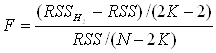 > F_{α,(2K-2),(N-2K)}

і не відхиляємо в супротивному разі. Рівень значущості критерію α.

На практиці спочатку застосовують критерій паралельності прямих, а потім вже, якщо гіпотеза Н₁ не відхиляється, перевіряють гіпотезу H₂ (вважаючи, що гіпотеза H₁ справелива), використовуючи статистику

.

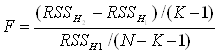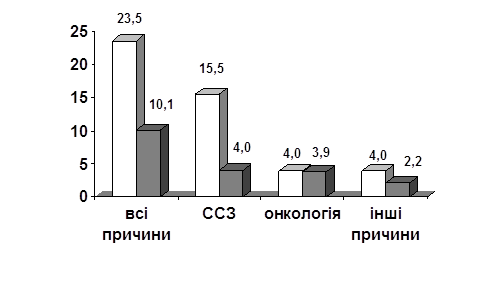
РОЗДІЛ 2. ДОСЛІДЖЕННЯ ЗАХВОРЮВАНОСТІ НА ТУБЕРКУЛЬОЗ, РАК, СНІД, ГЕПАТИТ А, ГЕПАТИТ Б

Похожие работы

Соціологічний аналіз молодіжної наркоманії в Україні

Скачать

138713

9

0

... притягають до себе різних кримінальних особистостей. І не випадково саме повії нерідко стають жертвами рекетирів, використовуються організованою злочинністю. Розділ 3. Соціологічний аналіз молодіжної наркоманії в Україні Сьогодні соціологи фіксують вагоме помолодіння різних форм девіантної поведінки. Тому виникає необхідність більш розгорнуто обдивиться проблему молодіжної наркоманії. ...

Статистичний облік природних ресурсів в Україні

Скачать

49793

18

5

... навантаження поділяються на показники антро­погенного та природного навантаження. Щоб оцінити антропо­генне навантаження на довкілля, застосовують показники: ·  видобутку (збору врожаю) окремих природних ресурсів; ·  що характеризують кiлькiсть викидів і скидів забруднюючих речовин та вiдходiв у атмосферне повітря, водні ресурси та в землю; ·  що характеризують кiлькiсть використовуваних ...

Динаміка профілю ризику серцево-судинних захворювань в жіночій популяції

Скачать

56321

2

4

... інгових тестів) та спільно з психотерапевтами коригувати тривожно-депресивні стани. СПИСОК ОПУБЛІКОВАНИХ ПРАЦЬ ЗА ТЕМОЮ ДИСЕРТАЦІЇ 1. Малацківська О.В. Динаміка профілю ризику серцево-судинних захворювань в жіночій популяції за 25-річний період // Кровообіг та гемостаз.– № 3. – 2006. – С. 49-52. 2. Малацківська О.В., Горбась І.М. Зв’язок традиційних факторів ризику серцево-судинних ...

Особливості клініки, діагностики, профілактики та лікування захворювань пародонта у вагітних із акушерською патологією

Скачать

51422

0

0

... А. В. Борисенко, О. О. Шекера // Матеріали ІІІ (Х) з’їзду Асоціації стоматологів України. – Полтава, 2008. – С. 136 АНОТАЦІЯ   Шекера О. О. Особливості клініки, діагностики, профілактики та лікування захворювань пародонта у вагітних із акушерською патологією. – Рукопис. Дисертація на здобуття наукового ступеня кандидата медичних наук за спеціальністю 14.01.22 – стоматологія. – Національний ...