Навигация
Производная и ее применение для решения прикладных задач
1. Производная и ее применение для решения прикладных задач
1.1 Исторические сведения
Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у Евклида. Ряд таких задач был решен Архимедом, разработавшим способ проведения касательной, примененный им к спирали, но применимый для других кривых. Основное понятие дифференциального исчисления – понятие производной – возникло в XVII в. В связи с необходимостью решения ряда задач из физики, механики и математики. Дифференциальное исчисление было создано Ньютоном и Лейбницем на основе двух задач: 1) о разыскании касательной к произвольной линии2) о разыскании скорости при произвольном законе движенияЕще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
|
|
Понятие производной
Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х0 - произвольная точка этого промежутка
Дадим аргументу x приращение ∆x, тогда функция y = f(x) получит приращение ∆y = f(x + ∆x) - f(x). Предел, к которому стремится отношение ∆y / ∆x при ∆x → 0, называется производной от функции f(x).
y'(x)=![]()
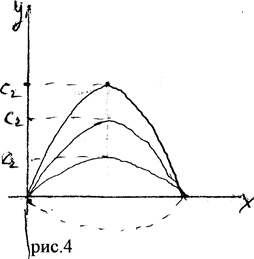
Геометрический смысл производной состоит в том, что она равна угловому коэффициенту касательной. Рассмотрим график функции ![]() (рис.). Видно,
(рис.). Видно,
что ![]() , т.е. это отношение равно угловому
, т.е. это отношение равно угловому
коэффициенту секущей mm. Если ![]() , то секущая,
, то секущая,
поворачиваясь вокруг точки М, в пределе переходит в
касательную ![]() , так как касательная является предельным
, так как касательная является предельным
положением секущей, когда точки пересечения сливаются.
Таким образом,![]()
![]() .
.
Уравнение касательной
![]() , где
, где ![]() - координаты точки касания, а
- координаты точки касания, а ![]() - текущие координаты точки касательной прямой.
- текущие координаты точки касательной прямой.
Физический смысл производной заключается в скорости изменения функции.
Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).
13 Дифференциал
Пусть дана функция ![]() и
и ![]() - внутренняя точка её области определения. Придадим аргументу приращение
- внутренняя точка её области определения. Придадим аргументу приращение ![]() и рассмотрим приращение функции
и рассмотрим приращение функции ![]()
Если это приращение ![]() можно представить в виде
можно представить в виде ![]() где величина
где величина ![]() не зависит от приращения
не зависит от приращения![]() , а
, а ![]() - бесконечно малая при
- бесконечно малая при ![]() величина, имеющая больший порядок малости, чем
величина, имеющая больший порядок малости, чем ![]() , то произведение
, то произведение ![]() называется дифференциалом функции
называется дифференциалом функции ![]() в точке
в точке ![]() и обозначается
и обозначается ![]() .
.
Перечень прикладных задач:
-составление уравнения касательной к графику функции;
-нахождение угла между пересекающимися прямыми, между графиками функций;
-исследование и построение графиков функций;
-решение задач на оптимум;
-преобразование алгебраических выражений;
-разложение многочлена на множители;
-доказательство тождеств;
-вычисление сумм;
-решение уравнений;
-приближенные вычисления и оценка погрешностей;
-доказательство неравенств и тождеств;
-решение систем уравнений;
-решение задач с параметрами;
-отбор кратных корней уравнения;
-сравнение величин;
-определение периода функции;
-нахождение пределов функции с помощью правила Лопиталя;
-разложение функций в ряд с помощью формулы Тейлора;
-приближенное решение уравнений методом проб, хорд и касательных;
-линеаризация алгебраических функций и многое другое.
3. Примеры решения прикладных задач
3.1 Исследование функций и построение их графиков
Пример 1
Исследовать и построить график функции
![]()
Решение.
1. Функция существует для всех ![]() .
.
Похожие работы
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...
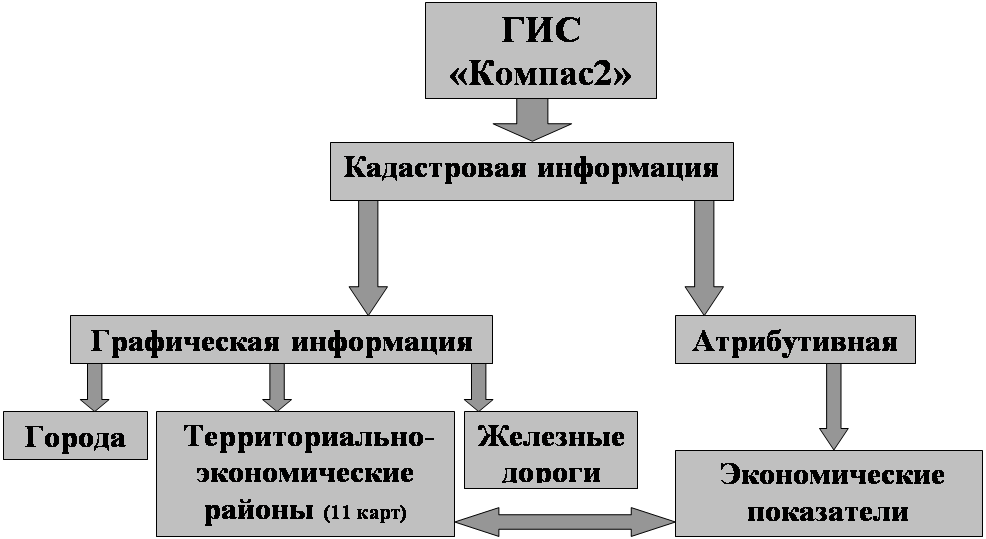
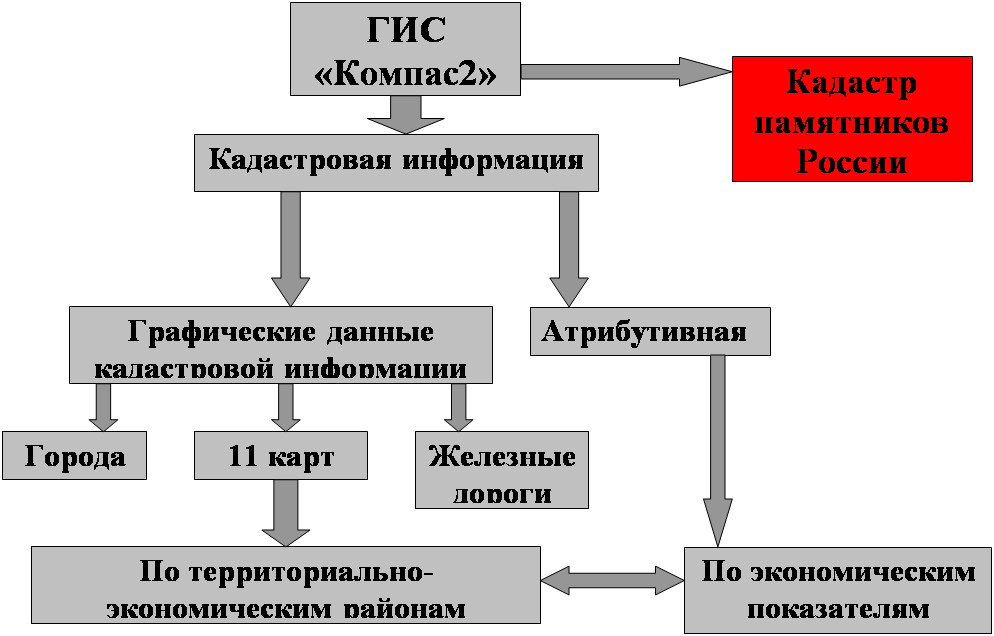
... кадастра памятников России и привязки его к ГИС «Компас-2», я изучил возможности, функции ГИС «Компас-2», а также возможность использования его для создания различных видов природных кадастров. Компас-2 – это сетевая система для представления, моделирования и анализа географической информации Функциональные возможности системы КОМПАС 2: публикация географической информации (ГИ) в сетях ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...

0 комментариев