Производная и ее применение для решения прикладных задач
Функция не является ни четной, ни нечетной
Определение периода функции
Разложение на множители и упрощение выражений
Решение неравенств
Решение уравнений
Вычисление пределов функции с помощью правила Лопиталя
Решение экономических задач
Задача о линеаризации функции
Навигация
Функция не является ни четной, ни нечетной
Производная и ее применение для решения прикладных задач
27370
знаков
0
таблиц
5
изображений
2. Функция не является ни четной, ни нечетной,
так как
,
то есть 
и 
.
3. В точке х=0 функция имеет разрыв в точке х=0.
При этом 
4. Находим производную: 
и приравниваем ее к нулю:
. Точка 
будет критической.
Проверим достаточные условия экстремума в точке . Так как знаменатель производной всегда положителен, то достаточно проследить за знаком числителя. Получаем: 
при 
и 
при 
. Следовательно, в точке функция имеет минимум, ее значение в точке 
.
5. Точек пересечения с осью ОY нет, так как данная функция не определена при х=0. Чтобы найти точки пересечения кривой с осью ОХ, нужно решить уравнение 
.
Тогда 
или 
.
Получим, что при 
функция убывает; х=
y=0; 
функция убывает; при 
функция убывает; при х=
функция имеет минимум y=3; при 
функция возрастает.
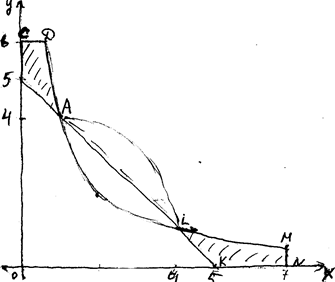
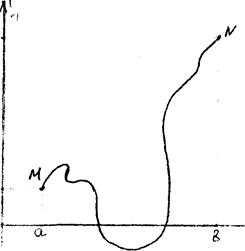
График данной функции представлен на рисунке.
Кривая, рассмотренная в этой задаче называется «Трезубец Ньютона».
3.2 Нахождение наибольшего и наименьшего значения функции, решение прикладных задач (задач на оптимум)
Пример 1
Из бревна, имеющего радиус R, сделать балку наибольшей прочности.
Решение:
Составляем функцию, выражающую необходимое условие.
В данной задаче высота балки (представляющей собой прямоугольник, вписанный в окружность радиуса R и ширины х), равна 
. Поэтому прочность такой балки равна 
. При этом х изменяется от 0 до 2R.
Функция обращается в нуль при х=0 и х=2R и положительна между этими значениями. Значит она имеет максимум, лежащий между 0 и 2R. Но производная этой функции 
обращается в нуль на отрезке 
лишь при 
. Это и есть оптимальное значение ширины b балки. Высота h балки такой ширины равна 
и отношение 
равно 
. Именно такое отношение высоты вытесываемой балки к ее ширине предписывается правилами производства строительных работ.
Пример 2
Требуется построить открытый цилиндрический резервуар вместимостью 
. Материал имеет толщину d. Какими должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим?
Решение.
Радиус основания внутреннего цилиндра обозначим через х, высоту внутреннего цилиндра через h. Объем дна и стенки резервуара
С другой стороны, по условию 
, откуда 
Подставляя в (*), находим
Полученную функцию 
нужно исследовать на экстремум при х>0:
Единственный положительный корень производной – это точка 
Она и дает решение задачи. При этом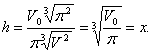 
Похожие работы
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...
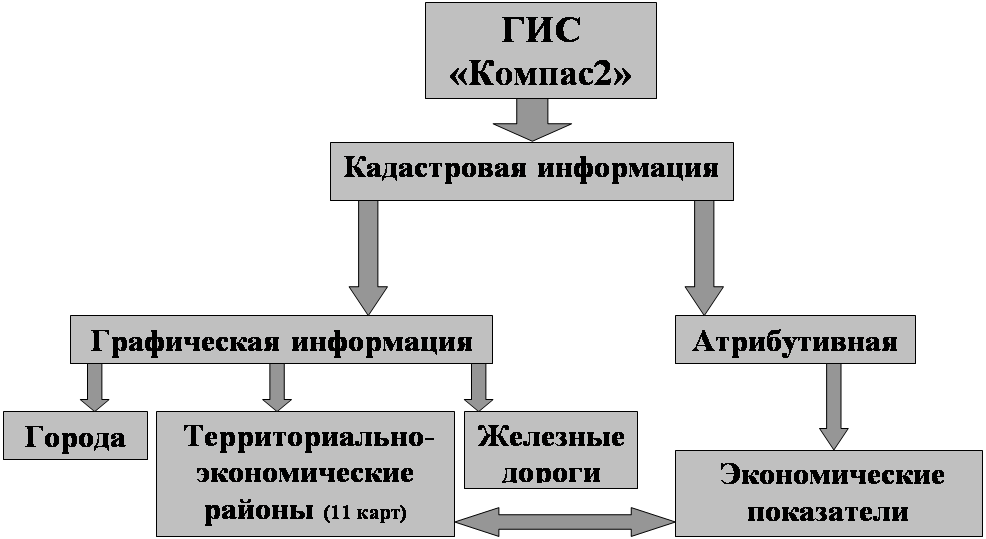
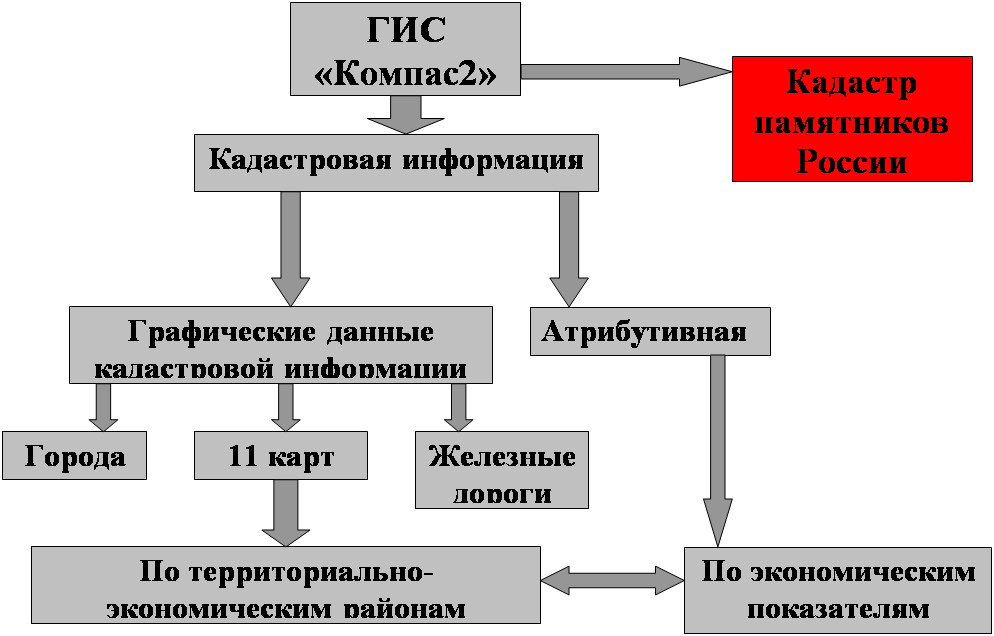
... кадастра памятников России и привязки его к ГИС «Компас-2», я изучил возможности, функции ГИС «Компас-2», а также возможность использования его для создания различных видов природных кадастров. Компас-2 – это сетевая система для представления, моделирования и анализа географической информации Функциональные возможности системы КОМПАС 2: публикация географической информации (ГИ) в сетях ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
0 комментариев