Навигация
Вычисление пределов функции с помощью правила Лопиталя
3.14 Вычисление пределов функции с помощью правила Лопиталя
Раскрытие неопределенностей типа ![]() и
и ![]() . Пусть однозначные функции
. Пусть однозначные функции ![]() и
и ![]() дифференцируемы при
дифференцируемы при ![]() причем производная
причем производная ![]() не обращается в нуль.
не обращается в нуль.
Если ![]() и
и ![]() - обе бесконечно малые или бесконечно большие при
- обе бесконечно малые или бесконечно большие при ![]() т.е. если частное
т.е. если частное ![]() представляет в точке х=
представляет в точке х=![]() неопределенность типа
неопределенность типа ![]() или
или ![]() , то
, то ![]() при условии, что предел отношения производных существует (правило Лопиталя). Правило применимо и в случае, когда
при условии, что предел отношения производных существует (правило Лопиталя). Правило применимо и в случае, когда ![]() .
.
Если частное ![]() вновь дает неопределенность в точке х=
вновь дает неопределенность в точке х=![]() одного из двух упомянутых типов и
одного из двух упомянутых типов и ![]() и
и ![]() удовлетворяют всем требованиям, ранее сформулированным для
удовлетворяют всем требованиям, ранее сформулированным для ![]() и
и ![]() , то можно перейти к отношению вторых производных и т.д.
, то можно перейти к отношению вторых производных и т.д.
Пример 1.
![]()
Пример 2.
Вычислить ![]() (неопределенность типа
(неопределенность типа ![]()
Приведя дроби к общему знаменателю, получим:
![]() (неопределенность типа
(неопределенность типа ![]()
Прежде чем применить правило Лопиталя, заменим знаменатель последней дроби эквивалентной ему бесконечно малой ![]()
Получим:
![]() (неопределенность типа
(неопределенность типа ![]()
По правилу Лопиталя
![]()
Далее, элементарным путем находим:
![]()
3.15 Решение физических задач, связанных с нахождением скорости, ускорения и т.д.
Пример 1.
Дано уравнение прямолинейного движения тела: ![]() , где S- путь, пройденный телом, м; t- время, с. Найдите скорость тела в момент времени t=1 c.
, где S- путь, пройденный телом, м; t- время, с. Найдите скорость тела в момент времени t=1 c.
Решение.
Скорость это производная пути по времени. Значит: ![]()
Подставив значение времени получим: ![]()
Пример 2.
Точка движется по закону ![]() . Найти скорость и ускорение через 2 с после начала движения (движение считать прямолинейным).
. Найти скорость и ускорение через 2 с после начала движения (движение считать прямолинейным).
Решение.
Скорость это производная пути по времени. Значит: ![]() .
.
Подставив значение времени получим ![]()
Пример 3.
Тело движется прямолинейно по закону ![]() Найти его кинетическую энергию через 5 с после начала движения, если масса тела 3 кг.
Найти его кинетическую энергию через 5 с после начала движения, если масса тела 3 кг.
Решение.
Формула нахождения кинетической энергии: ![]() .
.
Найдем скорость тела. ![]() ,
, ![]() .
.
Кинетическая энергия тела составит: ![]() .
.
Похожие работы
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...
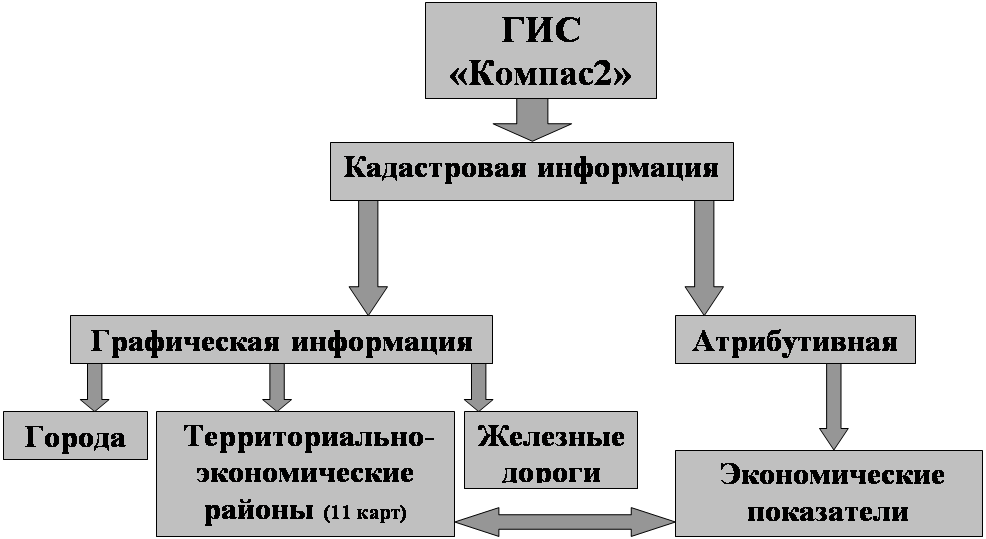
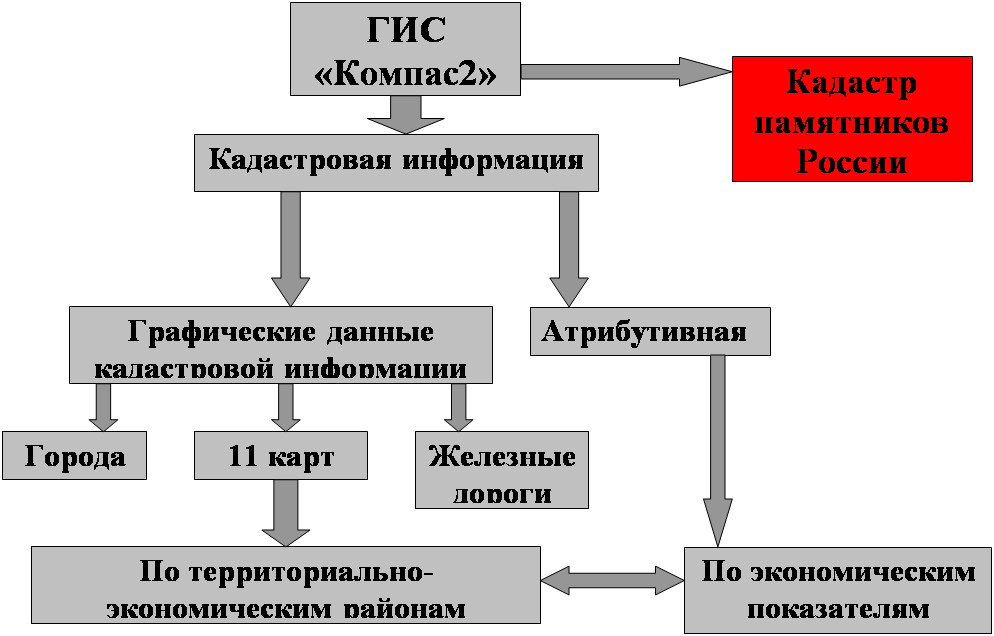
... кадастра памятников России и привязки его к ГИС «Компас-2», я изучил возможности, функции ГИС «Компас-2», а также возможность использования его для создания различных видов природных кадастров. Компас-2 – это сетевая система для представления, моделирования и анализа географической информации Функциональные возможности системы КОМПАС 2: публикация географической информации (ГИ) в сетях ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...

0 комментариев