Навигация
Определение периода функции
3.3 Определение периода функции
Пример 1.
Является ли периодической функция ![]() ?
?
Решение
Воспользуемся следующим утверждением: если дифференцируемая в каждой точке числовой прямой функция имеет период Т, то ее производная также имеет период Т.
Предположим, что данная функция ![]() является периодической с периодом Т. Применяя формулу
является периодической с периодом Т. Применяя формулу
![]() ,
,
получаем
![]() где
где ![]() .
.
Имеем
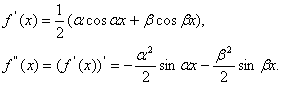
Поскольку по предположению функция ![]() имеет период Т, то функция
имеет период Т, то функция ![]() , а следовательно, и функция
, а следовательно, и функция ![]() также имеют период Т.
также имеют период Т.
Значит, и функция ![]()
Также имеет период Т. Отсюда следует, что существует число ![]() ,
, ![]() , такое, что Т=
, такое, что Т=![]() . Аналогично показывается, что существует число
. Аналогично показывается, что существует число ![]() , такое, что Т=
, такое, что Т=![]() .
.
Но тогда ![]()
т.е. число ![]() является рациональным, что неверно. Следовательно данная функция НЕ является периодической.
является рациональным, что неверно. Следовательно данная функция НЕ является периодической.
3.4 Нахождение приближенных значений функции
Пример 1.
Найти приращение и дифференциал функции в точке х=2 при ![]() и при
и при ![]() . Найдите абсолютную и относительные погрешности, которые мы допускаем при замене приращения функции ее дифференциалом.
. Найдите абсолютную и относительные погрешности, которые мы допускаем при замене приращения функции ее дифференциалом.
Решение
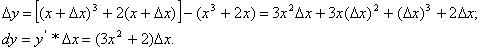
При х=2 и ![]() имеем
имеем
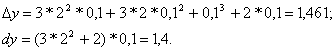
Абсолютная погрешность ![]()
Относительная погрешность ![]() то есть относительная погрешность будет около 4%.
то есть относительная погрешность будет около 4%.
При х=2 и ![]() имеем
имеем
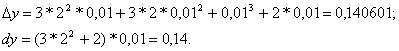
Абсолютная погрешность ![]() а относительная погрешность
а относительная погрешность ![]() то есть относительная погрешность будет уже около 0,4%.
то есть относительная погрешность будет уже около 0,4%.
Пример 2
Пользуясь понятием дифференциала функции вычислите приближенно изменение, претерпеваемое функцией ![]() при изменении х от значения 5 к значению 5,01.
при изменении х от значения 5 к значению 5,01.
Решение.
В данном случае будем считать х=5, а ![]() . Изменение функции
. Изменение функции
![]()
3.5 Нахождение величины угла между прямыми и кривыми.
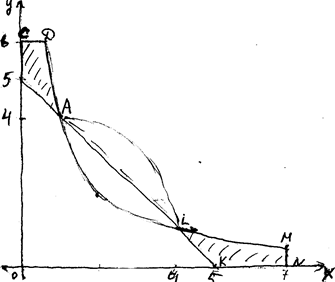
Углом между графиками функций ![]() и
и ![]() в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.).
в точке их пересечения называется угол между касательными к их графикам в этой точке (рис.).
Пример 1.
Найти угол между графиками функций ![]() и
и ![]()
в точке их пересечения (с положительной абсциссой).
Решение.
Абсциссы точек пересечения данных графиков удовлетворяют уравнению
![]()
И тем самым следующей системе: 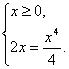
Отсюда находим, что графики функций пересекаются в двух точках, абсциссы которых равны 0 и 2. Найдем тангенсы углов наклона касательных к обоим графикам функций в точке с абсциссой, равной 2. Имеем
![]()
Отсюда ![]() и
и ![]() Так как
Так как ![]() , то уравнения касательных к графикам функций
, то уравнения касательных к графикам функций ![]() и
и ![]() в точке (2;2) соответственно имеют вид
в точке (2;2) соответственно имеют вид
![]() и
и ![]()
т.е.
![]() и
и ![]()
Следовательно величина угла ![]() между касательными удовлетворяют уравнению
между касательными удовлетворяют уравнению
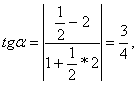
и тем самым графики функций ![]() и
и ![]() в точке с абсциссой х=2 пересекаются под углом, равным
в точке с абсциссой х=2 пересекаются под углом, равным ![]()
Похожие работы
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...
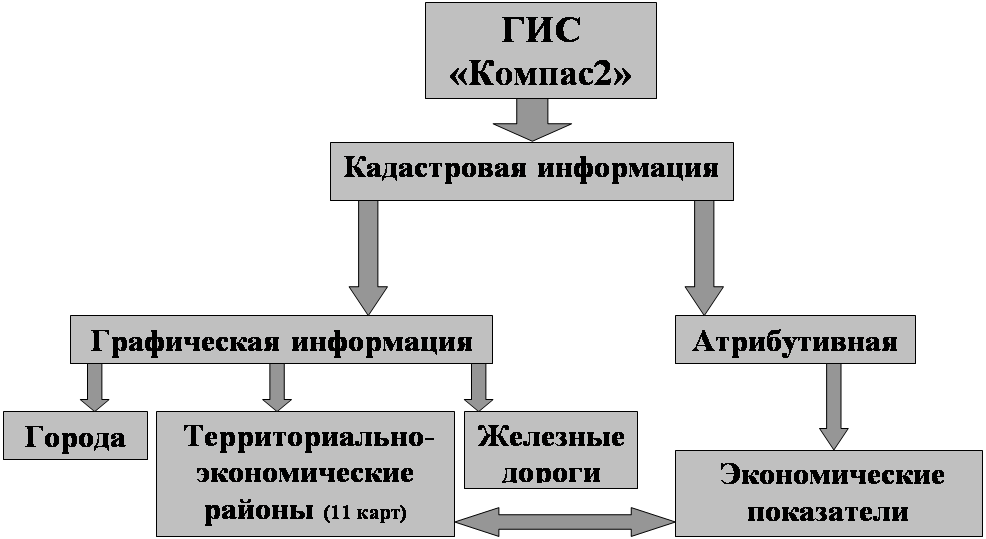
... кадастра памятников России и привязки его к ГИС «Компас-2», я изучил возможности, функции ГИС «Компас-2», а также возможность использования его для создания различных видов природных кадастров. Компас-2 – это сетевая система для представления, моделирования и анализа географической информации Функциональные возможности системы КОМПАС 2: публикация географической информации (ГИ) в сетях ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...

0 комментариев