Навигация
Використання обмеженості функції
33558
знаков
0
таблиц
12
изображений
2.2 Використання обмеженості функції
При рішенні рівнянь і нерівностей властивість обмеженості знизу або зверху функції на деякій множині часто відіграє визначальну роль.
Якщо існує число C таке, що для кожного 
виконується нерівність f (x) ≤ C, те функція f називається обмеженої зверху на множині D (малюнок 2).
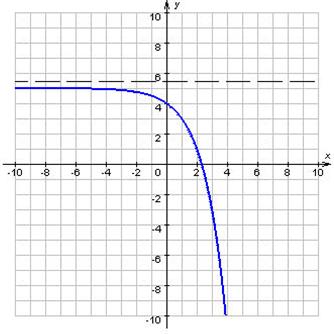
Малюнок 2
Якщо існує число c таке, що для кожного виконується нерівність f (x) ≥ c, те функція f називається обмеженої знизу на множині D (малюнок 3).
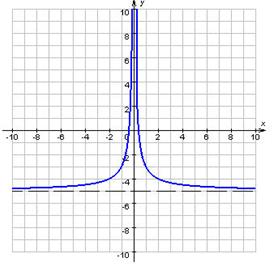
Малюнок 3
Функція, обмежена й зверху, і знизу, називається обмеженої на множині D. Геометрично обмеженість функції f на множині D означає, що графік функції y = f (x), лежить у смузі c ≤ y ≤ C (малюнок 4).
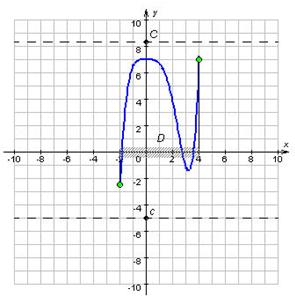
Малюнок 4
Якщо функція не є обмеженою на множині, то говорять, що вона не обмежена.
Прикладом функції, обмеженої знизу на всій числовій осі, є функція y = x2. Прикладом функції, обмеженої зверху на множині (–∞; 0) є функція y = 1/x. Прикладом функції, обмеженої на всій числовій осі, є функція y = sin x.
Приклад 2.2.1 Вирішите рівняння
sin(x3 + 2х2 + 1) = х2 + 2х + 2. (4)
Рішення. Для будь-якого дійсного числа х маємо sin(x3 + 2х2 + 1) ≤ 1, х2 + 2х + 2 = (x + 1)2 + 1 ≥ 1. Оскільки для будь-якого значення х ліва частина рівняння не перевершує одиниці, а права частина завжди не менше одиниці, то дане рівняння може мати рішення тільки при 
.
При 
, 
, тобто при рівняння (4) так само корінь не має .
Відповідь: O.
Приклад 2.2.2 Вирішите рівняння
. (5)
Рішення. Очевидно, що х = 0, х = 1, х = -1 є рішеннями даного рівняння. Для знаходження інших рішень у силу непарності функції f(х) = = x3 - x - sin πx досить знайти його рішення в області х > 0, х ≠ 1, оскільки якщо x0 > 0 є його рішенням, те й (-x0) також є його рішенням.
Розіб'ємо множину х > 0, х ? 1, на два проміжки: (0; 1) і (1; +?)
Перепишемо початкове рівняння у вигляді x3 - x = sin πx. На проміжку (0; 1) функція g(х) = x3 - x приймає тільки негативні значення, оскільки х3 < < х, а функція h(x) = sin πx тільки позитивні. Отже, на цьому проміжку рівняння не має рішень.
Нехай х належить проміжку (1; +∞). Для кожного з таких значень х функція g(х) = х3 - х приймає позитивні значення, функція h(x) = sin πx приймає значення різних знаків, причому на проміжку (1; 2] функція h(x) = sin ?x непозитивна. Отже, на проміжку (1; 2] рівняння рішень не має.
Якщо ж х > 2, то |sin πx| ≤ 1, x3 - x = x(x2 - 1) > 2∙ 3 = 6, а це означає, що й на проміжку (1; +∞) рівняння також не має рішень.
Отже, x = 0, x = 1 і x = -1 і тільки вони є рішеннями вихідного рівняння.
Відповідь: {-1; 0; 1}.
Приклад 2.2.3 Вирішите нерівність
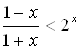. (6)
Рішення. ОПЗ нерівності є всі дійсні x, крім x = -1. Розіб'ємо ОПЗ нерівності на три множини: -? < x < -1, -1 < x ? 0, 0 < x < +? і розглянемо нерівність на кожному із цих проміжків.
Нехай -∞ < x < -1. Для кожного із цих x маємо g(x) =
< 0, а f(x) = 2x > 0. Отже, всі ці x є рішеннями нерівності.
Нехай -1 < x ≤ 0. Для кожного із цих x маємо g(x) = 1 - 
, а f(x) = 2x ≤ 1. Отже, жодне із цих x не є рішенням даної нерівності.
Нехай 0 < x < +∞. Для кожного із цих x маємо g(x) = 1 - 
, a 
. Отже, всі ці x є рішеннями вихідної нерівності.
Відповідь: 
.
Похожие работы
... допомогою цієї програми учень може сам перевіряти набуті знання, і вчитель може перевіряти знання певного учня. Вступ. МЕТА РОБОТИ - системазувати відомості про показникові та логарифмічні рівняння й нерівності та їх системи в шкільному курсі алгебри старшої школи і розкрити роль і місце вивчення показникових та логарифмічних рівняньта нерівностей в школі та вибрати методику подання цієї теми. ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний. 3. Не стандартні методи рішення ірраціональних рівнянь Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, ...
... і різної ширини смужок зі зворотньої сторони копії(несправність механізму термічного закріплення зображення). 5. Методи і технічні засоби дослідження документів на право водіння, володіння і користування автотранспортом При дослідженні документів виявлення і вивчення особливостей і ознак проводиться шляхом спостереження, тобто зорового сприйняття. Але при звичайних умовах спостереження і ...
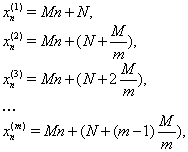
0 комментариев