Навигация
Використання симетричності рівняння
33558
знаков
0
таблиц
12
изображений
3.3 Використання симетричності рівняння
Іноді зовнішній вигляд рівняння - деяка його симетричність - підказує спосіб рішення рівняння.
Приклад 3.3.1 Вирішите рівняння
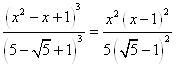. (11)
Рішення. Очевидно, що зовнішній вигляд рівняння підказує, що одне з корінь рівняння (11) є 
. Однак знайти інших корінь цього рівняння тут не так просто. Перепишемо рівняння (11) у трохи іншому виді.
Оскільки справедливі тотожні рівності
,
те рівняння (11) можна переписати так:
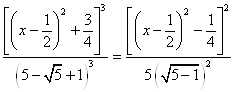. (12)
Тепер очевидно, що якщо 
― корінь рівняння (12), те 
також корінь рівняння (12), оскільки
. (13)
Покажемо, що якщо 
, є корінь рівняння (11), те 
також є корінь цього рівняння.
Дійсно, тому що
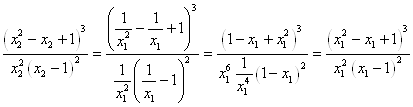
те звідси й випливає це твердження.
Отже, якщо , ― корінь рівняння (11), те воно має ще коріння
, 
, 
, 
,
т. е. рівняння (11) має корінь
, 
, 
, 
, 
, 
.
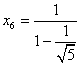Оскільки рівняння (11) є алгебраїчне рівняння шостого ступеня, то воно має не більше шести корінь. Таким чином, ми знайшли всі коріння рівняння (11).
Відповідь: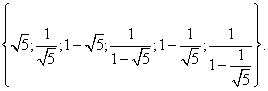 
3.4 Дослідження рівняння на проміжках дійсної осі
Іноді рішення рівняння можна знайти, досліджуючи його на різних числових проміжках.
Приклад 3.4.1 Вирішите рівняння
. (14)
Рішення. Перепишемо рівняння у вигляді 
або, використовуючи формулу різниці
, (15)
у вигляді
. (16)
Звідси видно, що одне з корінь даного рівняння є 
. Доведемо, що рівняння
(17)
рішень не має.
Розіб'ємо числову вісь на проміжки
Для будь-якого x із проміжку 
маємо, що ліва частина рівняння (17) позитивна, тому на цьому проміжку рівняння рішень не має.
Оскільки
,
те для будь-якого х із проміжку 
цей багаточлен позитивний. Це означає, що на проміжку рівняння (17) також не має рішень.
Оскільки
,
те для будь-якого x із проміжку 
цей багаточлен позитивний. Отже, і на проміжку рівняння (17) не має рішень.
Отже, дане рівняння (17) має єдине рішення .
Відповідь: {1}.
ВИСНОВОК
У процесі дослідження ціль дипломної роботи досягнута, повністю вирішені поставлені задачі й отримані наступні результати й висновки:
Наведено відомості про давнину постановки перед людиною задачі рішення рівнянь і нерівностей.
Наведено й розглянуті на прикладі методи рішення рівнянь і нерівностей, засновані на використанні властивостей функції.
Розглянуто й випробувані додаткові нестандартні методи рішення рівнянь і нерівностей.
Продовження дослідження може полягати у вивченні застосування властивостей синуса й косинуса, застосуванні похідній, використанні числових нерівностей, використанні графіків і інших нестандартних способів рішення рівнянь і нерівностей.
ДОДАТОК
Задачі для самостійного рішення:
Доведіть, що наступне рівняння не має рішень:
.
.
.
.
Вирішите рівняння:
Відповідь: {0}.
.
Відповідь: {2}.
.
Відповідь: {-1}.
.
Відповідь: {2}.
.
Відповідь: {1}.
.
Відповідь: {1; -2}.
Відповідь: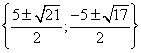 
.
.
Відповідь: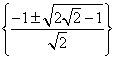 
Вирішите нерівність:
.
Відповідь: 
.
.
Відповідь: .
.
Відповідь: 
.
.
Відповідь: 
.
.
Відповідь: 
СПИСОК ДЖЕРЕЛ
1. Абилкасимова А. Є. Алгебра 10 клас. – К., 2003
2. Алилов М. А., Колягин Ю. М. і ін. Алгебра й начало аналізу. – К., 2004
3. Болтянський В. Г., Сидоров Ю. В., Шабунин М. І. Лекції й задачі по елементарній математиці. – К., 2006
4. Газета «Математика» №20, 2008 р.
5. Голубєв В. і. Рішення складних і нестандартних задач по математиці. – К., 1995
6. Горштейн П. І. Задачі з параметрами., - К., 1999.
7. Гусєв В. А., Мордович О. Г. Математика. Довідкові матеріали. – К., 2001
8. Далингер В. А. Нестандартні рівняння й методи їхнього рішення. –К., 2005
9. Жафяров А. Ж. Профільне навчання старшокласників. К., 2001
10. Журнал «Математика в школі», 1999-2007 р.
11. Івлєв Б. М., Абрамов А. М., Дудницин Ю. П., Швардцбурд С. І. Задачі підвищених труднощів по алгебрі й початкам аналізу. – К., 2005.
12. Ковальова Г. И., Конкина Е. В. Функціональний метод рішення рівнянь і нерівностей. – К., 2006
13. Кравцов С. В. Методи рішення задач по алгебрі. – К., 2001
14. Кулагін Є. Д. 300 конкурсних задач по математиці. - К., 2003
15. Кушнір А. І. Математична енциклопедія. - К.,1995 р.
16. Литвиненко В. Н., Мордкович А. Г. Практикум по елементарній математиці. Алгебра. Тригонометрія. – К., 1991 р.
Похожие работы
... допомогою цієї програми учень може сам перевіряти набуті знання, і вчитель може перевіряти знання певного учня. Вступ. МЕТА РОБОТИ - системазувати відомості про показникові та логарифмічні рівняння й нерівності та їх системи в шкільному курсі алгебри старшої школи і розкрити роль і місце вивчення показникових та логарифмічних рівняньта нерівностей в школі та вибрати методику подання цієї теми. ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний. 3. Не стандартні методи рішення ірраціональних рівнянь Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, ...
... і різної ширини смужок зі зворотньої сторони копії(несправність механізму термічного закріплення зображення). 5. Методи і технічні засоби дослідження документів на право водіння, володіння і користування автотранспортом При дослідженні документів виявлення і вивчення особливостей і ознак проводиться шляхом спостереження, тобто зорового сприйняття. Але при звичайних умовах спостереження і ...
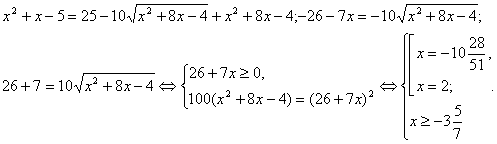
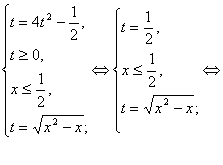
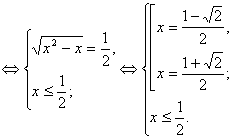
0 комментариев