Навигация
Використання періодичності функції
33558
знаков
0
таблиц
12
изображений
2.3 Використання періодичності функції
Функція f (x) називається періодичної з періодом T ≠ 0, якщо виконуються дві умови:
якщо 
, то x + T і x – T також належать області визначення D (f (x));
для кожного виконана рівність
f (x + T) = f (x).
Оскільки 
те з наведеного визначення треба, що
Якщо T – період функції f (x), то очевидно, що кожне число nT, де 
, n ≠ 0, також є періодом цієї функції.
Найменшим позитивним періодом функції називається найменше з позитивних чисел T, що є періодом даної функції.
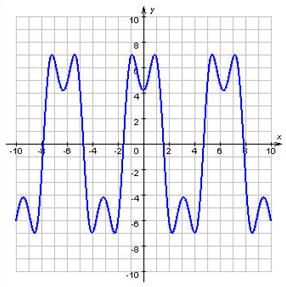
Графік періодичної функції
Графік періодичної функції звичайно будують на проміжку [x0; x0 + T), а потім повторюють на всю область визначення.
Гарним прикладом періодичних функцій можуть служити тригонометричні функції y = sin x, y = cos x (період цих функцій дорівнює 2π), y = tg x (період дорівнює π) і інші. Функція y = const також є періодичною. Для неї періодом є будь-яке число T ≠ 0.
На закінчення відзначимо властивості періодичних функцій. [19]
Якщо f (x) – періодична функція з періодом T, то функція
g (x) = A · f (kx + b)
де k ≠ 0 також є періодичною з періодом 
.
Нехай функції f1 (x) і f2 (x) визначені на всій числовій осі і є періодичними з періодами T1 > 0 і T2 > 0. Тоді якщо 
те функція 
періодична з періодом T, рівним найменшому загальному кратному чисел T1 і T2.
Приклад 2.4.1 Функція 
періодична з періодом T = 5. Відомо, що 
. Знайдіть
Рішення. Перетворимо окремо кожний доданок:
Тоді 
Відповідь: 2.
Приклад 2.4.2 [24] Знайдіть період функції
Рішення. Перетворимо дане вираження:
має період 
;
має період 
.
Тоді функція має період
Відповідь: ?.
Приклад 2.4.3 Нехай 
- періодична функція з періодом 3 така, що
; 
.
Вирішите рівняння:
(7)
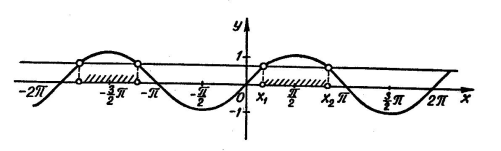
Графік функції на множині [0;3) зображений на малюнку 3:
|
|
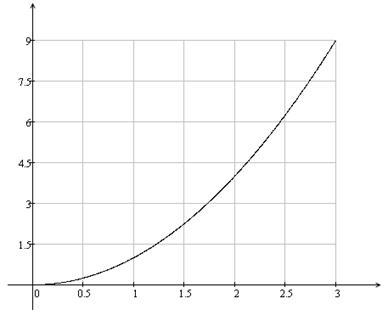
Малюнок 5
Таким чином 3 - період функції , те
, тоді рівняння (7) прикмет вид 
, розглянемо два випадки.
1) нехай 
, тобто 
, тоді рівняння прийме вид:
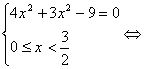
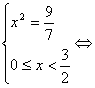
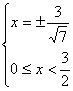, значить 
і виходить
,
2) нехай
те
, тоді 
рівняння прийме вид:
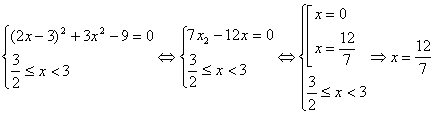; отже 
, 
таким чином 
, 
.
Відповідь: 
.
Похожие работы
... допомогою цієї програми учень може сам перевіряти набуті знання, і вчитель може перевіряти знання певного учня. Вступ. МЕТА РОБОТИ - системазувати відомості про показникові та логарифмічні рівняння й нерівності та їх системи в шкільному курсі алгебри старшої школи і розкрити роль і місце вивчення показникових та логарифмічних рівняньта нерівностей в школі та вибрати методику подання цієї теми. ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний. 3. Не стандартні методи рішення ірраціональних рівнянь Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, ...
... і різної ширини смужок зі зворотньої сторони копії(несправність механізму термічного закріплення зображення). 5. Методи і технічні засоби дослідження документів на право водіння, володіння і користування автотранспортом При дослідженні документів виявлення і вивчення особливостей і ознак проводиться шляхом спостереження, тобто зорового сприйняття. Але при звичайних умовах спостереження і ...
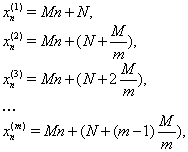
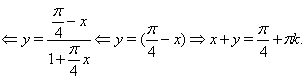
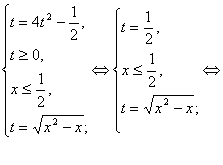
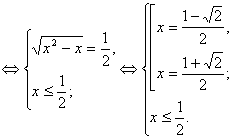
0 комментариев