Навигация
ДЕЯКІ ШТУЧНІ СПОСОБИ РІШЕННЯ РІВНЯНЬ
33558
знаков
0
таблиц
12
изображений
3 ДЕЯКІ ШТУЧНІ СПОСОБИ РІШЕННЯ РІВНЯНЬ
Існують і інші нестандартні методи рішення рівнянь і нерівностей, крім використання властивостей функції. Дана глава присвячена додатковим методам рішення.
3.1 Множення рівняння на функцію
Іноді рішення алгебраїчного рівняння істотно полегшується, якщо помножити обидві його частини на деяку функцію - багаточлен від невідомої. При цьому треба пам'ятати, що можливо появу зайвих корінь - корінь багаточлена, на який множили рівняння. Тому треба або множити на багаточлен, що не має корінь, і одержувати рівносильне рівняння, або множити на багаточлен, що має корінь, і тоді кожний з таких корінь треба обов'язково підставити у вихідне рівняння й установити, чи є це число його коренем.
Приклад 3.1.1 Вирішите рівняння
. (1)
Рішення. Помноживши обидві частини рівняння на багаточлен 
, що не має корінь, одержимо рівняння
, (2)
рівносильне рівнянню (1). Рівняння (2) можна записати у вигляді
. (3)
Ясно, що рівняння (3) не має дійсних корінь, тому й рівняння (1) їх не має.
Відповідь: O.
Приклад 3.1.2 [19] Вирішите рівняння
. (4)
Рішення. Помноживши обидві частини цього рівняння на багаточлен 
, одержимо рівняння
, (5)
Є наслідком рівняння (4), тому що рівняння (5) має корінь 
, що не є коренем рівняння (4).
Рівняння (5) є симетричне рівняння четвертого ступеня. Оскільки 
не є коренем рівняння (5), те, розділивши обидві його частини на 
й перегрупувавши його члени, одержимо рівняння
(6)
рівносильне рівнянню (5). Позначивши 
, перепишемо рівняння (6) у вигляді
. (7)
Рівняння (7) має два корені: 
і 
. Тому рівняння (6) рівносильне сукупності рівнянь
и.
Вирішивши кожне із цих рівнянь, знайдемо чотири корені рівняння (6), а тим самим і рівняння (5):
, 
, 
, 
Тому що корінь є стороннім для рівняння (4), те звідси одержуємо, що рівняння (4) має три корені: x1, x2, x3.
Відповідь: 
3.2 Угадування кореня рівняння
Іноді зовнішній вигляд рівняння підказує, яке число є коренем рівняння.
Приклад 3.2.1 Вирішите рівняння
. (8)
Рішення. Перепишемо рівняння (8) у вигляді:
. (9)
Із зовнішнього вигляду цього рівняння очевидно, що х = 12 є його корінь. Для знаходження інших корінь перетворимо багаточлен
Тому що багаточлен 
не має корінь, те вихідне рівняння має єдиний корінь х = 12.
Відповідь: {12}.
Приклад 3.2.2. Вирішите рівняння
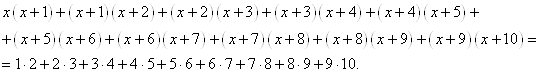(10)
Рішення. Легко помітити, що 
і 
є рішеннями цього рівняння. Після розкриття дужок це рівняння перепишеться як квадратне. А це означає, що воно може мати не більше двох корінь. Тому що два корені цього рівняння знайдені, те тим самим воно й вирішено.
Відповідь: 
Похожие работы
... допомогою цієї програми учень може сам перевіряти набуті знання, і вчитель може перевіряти знання певного учня. Вступ. МЕТА РОБОТИ - системазувати відомості про показникові та логарифмічні рівняння й нерівності та їх системи в шкільному курсі алгебри старшої школи і розкрити роль і місце вивчення показникових та логарифмічних рівняньта нерівностей в школі та вибрати методику подання цієї теми. ...
... , рівняння прийме вид: Очевидно, що , для всіх і Отже, останнє рівняння рівносильне системі: Тим самим, ми довели, що при , рівняння має єдине рішення. Відповідь. . тригонометричний рівняння комбінований графічний Рішення з дослідженням функції Приклад [??] Доведіть, що всі рішення рівняння і- цілі числа. Рішення. Основний період вихідного рівняння дорівнює . Тому ...
... Зауваження. Отже, при рішенні рівнянь із радикалами потрібне вміти користуватися кожним із цих методів і вибирати в кожному випадку оптимальний. 3. Не стандартні методи рішення ірраціональних рівнянь Існують ірраціональні рівняння, які вважаються для школярів звичайних освітніх шкіл задачами підвищених труднощів. Для рішення таких рівнянь краще застосовувати не традиційні методи, а прийоми, ...
... і різної ширини смужок зі зворотньої сторони копії(несправність механізму термічного закріплення зображення). 5. Методи і технічні засоби дослідження документів на право водіння, володіння і користування автотранспортом При дослідженні документів виявлення і вивчення особливостей і ознак проводиться шляхом спостереження, тобто зорового сприйняття. Але при звичайних умовах спостереження і ...
0 комментариев