Навигация
Характеристическое свойство квази-средних
31605
знаков
0
таблиц
0
изображений
2. Характеристическое свойство квази-средних
Теперь мы готовы для квази-средних указать упомянутое выше аксиоматическое определение. Будем исходить от частных случаев – простейших средних. Так взвешенные среднее арифметическое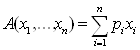 
и среднее геометрическое 
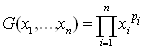можно определить как непрерывные хотя бы в одной точке решения функциональных уравнений 
и 
соответственно, а также эти решения должны удовлетворять условию усреднения, иначе не обязательно 
и 
. Первое условие есть результат теоремы 1, а второе условие мы докажем далее в общем случае.
Заметим, что операцию умножения, которая используется в уравнении для среднего геометрического, можно представить как 
, где 
, то есть функция, задающая среднее геометрическое. Операция сложения в уравнении для среднего арифметического представляется аналогично, но с функцией
.
Тогда вообще для квази-средних рассмотрим операцию, обобщающую сложение и умножение, 
, где 
– произвольная непрерывная, строго монотонная функция, множество значений которой – один из промежутков (–
;а), (–;а], (b; ), [b; ), (–;), где a≤0 и b≥0, что гарантирует существование операции для любых x и y из области определения функции 
. Сформулируем общий
результат, выражающий аксиоматическое определение квази-средних [1].
Теорема 2. Квази-средние – это такие функции 
от n переменных, для которых выполнены условия:
1) непрерывность хотя бы в одной точке;
2) 
;
3) 
.
Доказательство. Очевидно, что квази-средние, ранее определённые как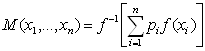 
удовлетворяют перечисленным свойствам. Важно показать обратное – других величин с данными свойствами не существует. Для этого выведем вид функций , исходя из указанных условий.
Распишем уравнение 
, используя определение операции 
:
=
=
,
=
=
Далее, если определить 
и обозначить 
, 
, то последнее
выражение перепишется так
, где функция H непрерывна хотя бы в одной точке. Тогда единственной такой функцией будет 
, pi
R. Возвращаясь к прежним переменным и функциям, найдём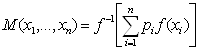 
,
piR.
Осталось показать, что и 
. Используем свойство усреднения найденного решения: .
Возьмём 
, но тогда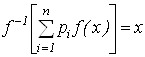 
или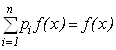 
, и поэтому 
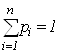. А если предположить, что какое-то 
, то для 
и 
, 
имеем
=
=
=
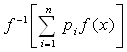, что противоречит условию.
Аналогично можно определить квази-средние вида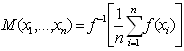 
.
Теорема 3. Квази-средние вида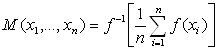 
– это такие функции от n переменных, для которых выполнены условия:
1) непрерывность хотя бы в одной точке;
2) ;
3) рефлексивность, то есть 
;
4) симметричность.
Действительно, свойства 1 и 2 выделяют функции 
, piR, далее свойство 3 обеспечивает , а из свойства 4 вытекает
.
Теперь мы можем аксиоматически задавать частные случаи квази-средних, указывая для них свои операции в функциональном уравнении . Например:
для среднего арифметического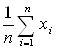 
задающая его функция 
, и поэтому 
;
для среднего геометрического 
, 
;
для среднего гармонического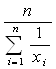 
, 
;
для среднего квадратичного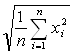 
, 
.
Похожие работы
... рассматриваться как определенные независимо одна от другой. Зависимость между силой, массой и ускорением. Второй закон Ньютона Данную зависимость с точностью, которая возможна в демонстрационном эксперименте, устанавливают на опыте, Поскольку согласно принятой в стабильном учебнике методике сначала устанавливается только способ задания некоторой силы «безразлично какой именно!», в опытах ...
... учетной информации; - порядок контроля за хозяйственными операциями. Таким образом, отчетность организации представляет собой единую систему информации об ее имущественном и финансовым положении. 2. Анализ финансово - хозяйственной деятельности предприятия (на примере СП «Энергосбыт») 2.1 Технико-экономическая характеристика предприятия СП «Энергосбыт» - филиала ОАО «РЖД» Куйбышевская ...
... politique, ou Simple exposition de la maniere dont se forment, se distribuent et se consomment les richesses»] (1803) Ж. Б. Сэ был крупнейшим представителем классической школы во Франции. Из всех представителей классической политической экономии он, пожалуй, удостоился наиболее яростной критики представителей многих еретических направлений в экономической науке - от марксистов до кейнсианцев. ...
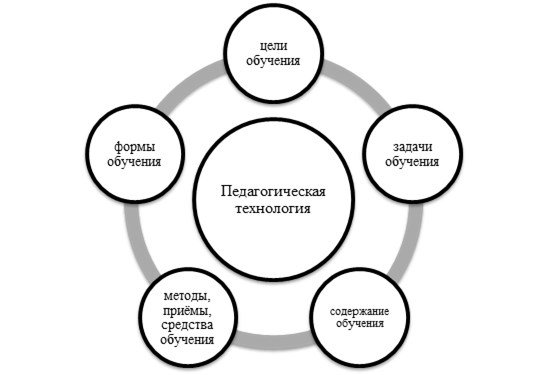
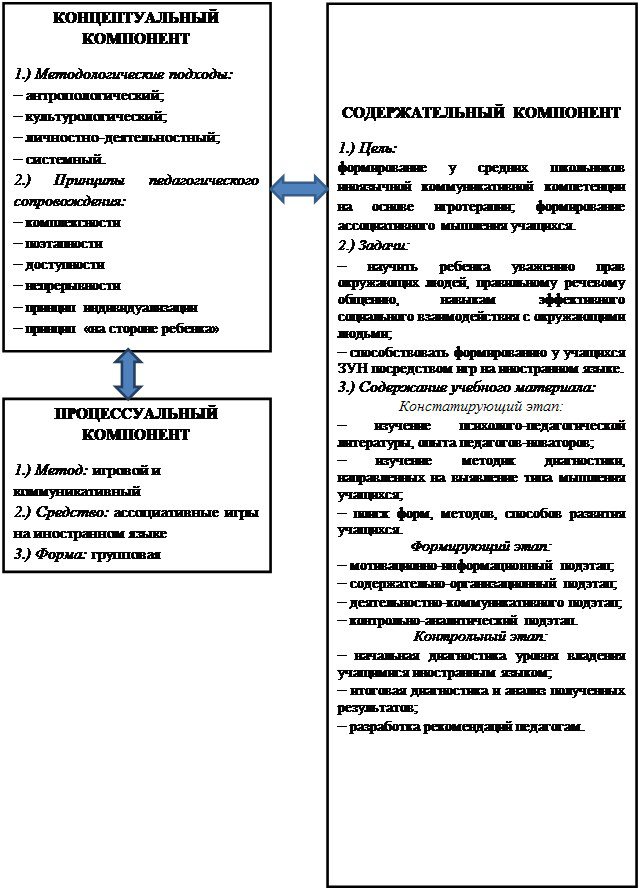
... являются временные структуры коры головного мозга, возникающие при одновременном или последовательном воздействии двух или более раздражителей [31, с. 162].1.2 Психолого-педагогические предпосылки формирования ассоциативного мышления у учащихся средней школы В подростковом возрасте происходит развитие способностей, процессов мышления, приводящее к росту сознания, воображения, суждений и интуиции ...
0 комментариев