Навигация
Тождественные квази-средние
31605
знаков
0
таблиц
0
изображений
3. Тождественные квази-средние
Квази-среднее 
определено, если задана функция 
. Возникает естественный вопрос, справедливо ли обратное предложение: если 
для любых 
или 
и 
–тождественны, то следует ли отсюда, что задающие их функции 
и 
также тождественны. Ответ на этот вопрос даёт следующая
Теорема 4. Необходимым и достаточным условием тождественности квази-средних 
и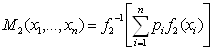 
является условие 
, где 
.
Доказательство. Если указанное условие выполняется, то
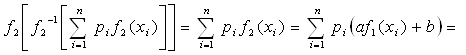
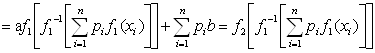, и поэтому
=
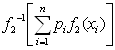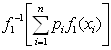или 
=
для любых 
, то есть условие достаточно.
Обратно, пусть 
=
, 
=
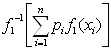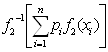или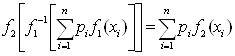 
. Обозначая 
и 
, перепишем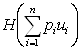 
=
.
Сведём это равенство к функциональному уравнению. Возьмём точку 
из области значений функции и представим 
. Тогда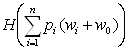 
=
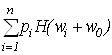или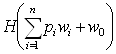 
=
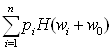. Полагая 
, где 
для каждого i, найдём 
=
, где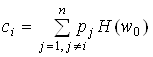
не зависит от 
.
Поэтому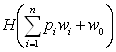 
=
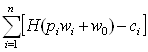, что с обозначениями 
, 
, 
перепишется так: 
.
Тогда решением этого функционального уравнения будет функция 
, 
, где 
. Так как 
, то 
, или
, если взять 
.
Таким образом, чтобы задать одно и то же квази-среднее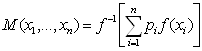 
мы можем взять любую функцию из целого класса функций 
, где а≠0 и b – произвольные постоянные, и другого способа получить тождественные квази-средние не существует.
Похожие работы
... рассматриваться как определенные независимо одна от другой. Зависимость между силой, массой и ускорением. Второй закон Ньютона Данную зависимость с точностью, которая возможна в демонстрационном эксперименте, устанавливают на опыте, Поскольку согласно принятой в стабильном учебнике методике сначала устанавливается только способ задания некоторой силы «безразлично какой именно!», в опытах ...
... учетной информации; - порядок контроля за хозяйственными операциями. Таким образом, отчетность организации представляет собой единую систему информации об ее имущественном и финансовым положении. 2. Анализ финансово - хозяйственной деятельности предприятия (на примере СП «Энергосбыт») 2.1 Технико-экономическая характеристика предприятия СП «Энергосбыт» - филиала ОАО «РЖД» Куйбышевская ...
... politique, ou Simple exposition de la maniere dont se forment, se distribuent et se consomment les richesses»] (1803) Ж. Б. Сэ был крупнейшим представителем классической школы во Франции. Из всех представителей классической политической экономии он, пожалуй, удостоился наиболее яростной критики представителей многих еретических направлений в экономической науке - от марксистов до кейнсианцев. ...
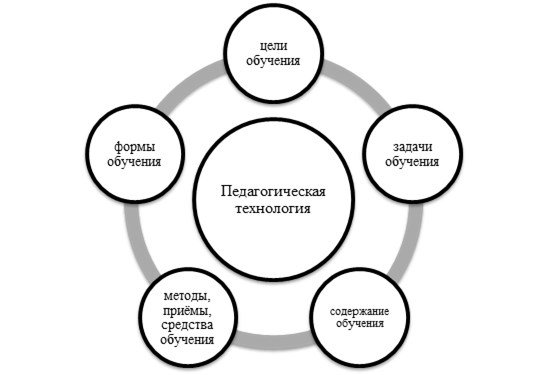
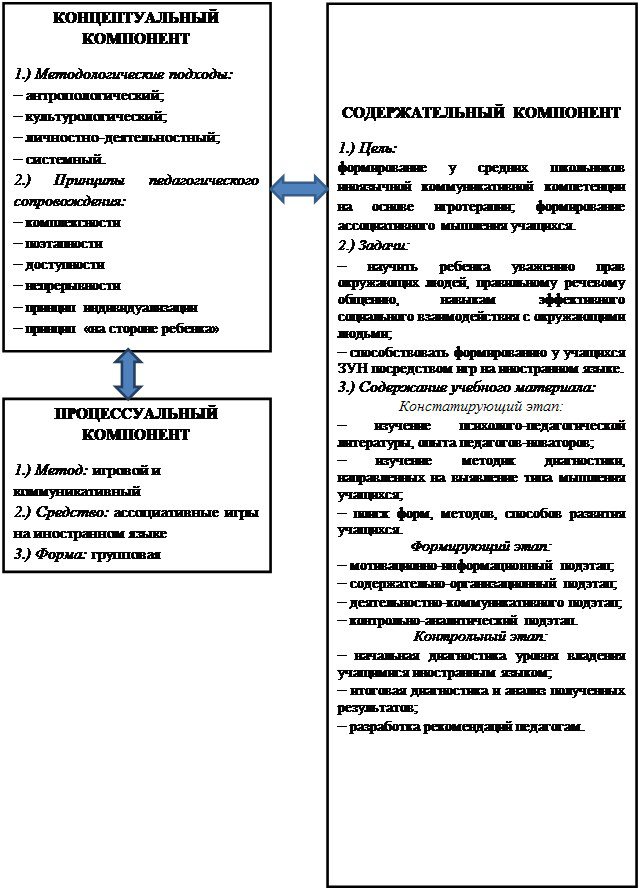
... являются временные структуры коры головного мозга, возникающие при одновременном или последовательном воздействии двух или более раздражителей [31, с. 162].1.2 Психолого-педагогические предпосылки формирования ассоциативного мышления у учащихся средней школы В подростковом возрасте происходит развитие способностей, процессов мышления, приводящее к росту сознания, воображения, суждений и интуиции ...
0 комментариев