Производная и дифференциал
Геометрические изложения и дифференцированные исчисления (построение графиков)
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
Неопределенный интеграл
Результат интегрирования проверим дифференцированием. Для этого найдем производную
Функции нескольких переменных, дифференцированных исчислений
Навигация
Производная и дифференциал
Пределы последовательностей и функций
18636
знаков
4
таблицы
6
изображений
2. Производная и дифференциал
Пусть функция 
определена в некоторой окрестности точки 
.
Производной функции в точке называется предел отношения 
, когда 
(если этот предел существует). Производная функции в точке обозначается
.
Например, выражение 
следует понимать как производную функции 
в точке 
.
Определение производной можно записать в виде формулы
. (4.1)
Предел (4.1) может не существовать. В этом случае говорят, что функция 
не имеет производной в точке . Если предел (4.1) равен 
, то говорят, что функция имеет в точке бесконечную производную.
В различных задачах (в том числе и экономических) производная функции интерпретируется как скорость изменения величины y относительно x. Геометрический смысл производной состоит в том, что 
– это тангенс угла наклона касательной к графику в точке 
.
Нахождение производной функции называется дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.
Укажем правила дифференцирования, которые сводят вычисление производных одних функций к вычислению производных других (более простых) функций.
Если функции 
дифференцируемы в точке , то сумма, разность, произведение и частное этих функций также дифференцируемы в точке , и справедливы следующие формулы
.
Если функция имеет обратную функцию 
и в точке производная 
, то обратная функция 
дифференцируема в точке 
и 
или 
.
Если функция дифференцируема в точке 
и 
, то сложная функция 
также дифференцируема в и верна следующая формула
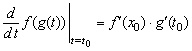или 
.
Пример.
Найти производную функции 
Решение:
Похожие работы
... знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны. Для упрощения задачи нахождения предела последовательности, вышеуказанного вида, мы прибегаем к помощи теоремы Штольца. Теорема Штольца Для определения пределов неопределённых выражений типа часто бывает полезна следующая теорема, принадлежащая Штольцу (O. Stolz). Теорема: Пусть варианта , ...
... такому произведению будет соответствовать свертка. Другими словами, выходной процесс системы, на которую действуют управляющее и возмущающее воздействия со своими передаточными функциями и , в действительной области можно представить в виде , . 5 Графические представления частотных характеристик Как уже отмечалось, частотные представления являются основой классических методов теории ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
0 комментариев